Расчет оптических потерь и основные характеристики приемника параболоцилиндрической установки со стационарным концентратором

В настоящее время проблема применения концентраторов заключается в решении задач повышения их оптической эффективности и обеспечения экономической рентабельности в эксплуатации.

В данной статье приводятся расчет оптических потерь и основные характеристики приемника параболоцилиндрической установки со стационарным концентратором.

Оптические потери, солнечного параболоцилиндрического концентратора в первую очередь, связаны радиационными свойствами поверхности отражателя, прозрачной изоляции и поглощающей поверхности приемника. Отражательная способность R зависит от природы поверхности и ее шероховатости. Для большинства практически используемых зеркальных покрытий R 3 равна 0,76 ^ 0,9, а в некоторых случаях достигает 0,94 ^ 0,96. Пропускательная способность прозрачной изоляций Т с и поглощательная способность поверхности приемника A_s (приведенная поглощательная способность) также зависят от материала и средних углов падения радиации. Угол падения отраженного луча на приемник зависит от места отражения луча на поверхности концентратора и от формы приемника. Точное значение произведения Т с • A s получается интегрированием по всему концентратору потока радиации, проходящего через прозрачное покрытие и падающего на приемник. Для практических расчетов можно принимать среднее значение этих коэффициентов. Коэффициент пропускания большинства практически применяемых прозрачных изоляции из термостойкого стекла составляет 0,85 ^ 0,92, а просветленных - достигает 0,94 ^ 0,96. Коэффициент поглощения черно окрашенной и селективно окрашенной поверхности приемника колеблется в пределах 0,85 ^ 0,96 Оптические потери, связанные с непопадающей частью фокусируемой радиации на приемнике ограниченного размера, оцениваются коэффициентом улавливания Y (фактор формы).

Коэффициент улавливания Y можно оценить по кривой нормального распределения плотности потока в фокальной плоскости, используя следующую формулу [1]:

Y =  2  гh(b / B) e_ h2(b/ Bf . d fhr 1’ k B J

-rr •⁰

где: b - расстояние от центра нормального фокального изображения; h -коэффициент нормального распределения связанной с максимальной плотностью потока в центре фокального пятна зависимостью h = Emax • B ^

Для решения уравнения (1) можно использовать таблицы интегралов вероятности

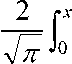
e

x

• dx ;

подставляя предел

x = h ( b / B ) , получим

значения Y для определенных отношений ширин и h. Таким образом, исходя из выбранного значения h (или из значения, более или менее соответствующего практически существующему отражателю) можно определить кривую распределения плотности потока энергии и вычислить значение Y в зависимости b / B. Например, при h = 60 приемник имеет ширину, составляющую 0,01 и 0,02 от ширины концентратора. При b/B = 0,01 предел интегрирования вероятности равен 60/(0,01) = 0,60. Из таблицы интегралов вероятности находим Y = 0,604. Для удвоенной ширины предел равен 1,2 и Y=0,91.

При расчете оптических потерь необходимо также учитывать затенение поверхности концентратора приемником. Это можно оценить коэффициентом затенения, определяемый по следующей формуле:

к ЗАТ = ( B - d H ) / B ,                (3)

где: d_H - наружный диаметр приемника.

Таким образом, для постоянных оптических коэффициентов (оптические коэффициенты R3 -тс • As • у приняты постоянными условно, так как они изменяются в течение срока службы коллектора) коллектора можно записать следующее выражение:

С опт = R 3-Тс • A s • Y • К зат .         (4)

Оптические потери происходят также в результате падения прямых солнечных лучей не по нормали к поверхности коллектора и связанные с этим концевых эффектах. Косинус угла падения cos 0 (угол между нормалью коллектора и лучами солнца) зависит от способа ориентации коллектора и определяет эффективность системы при одноосевом слежении. В случае двухосевого слежения коллектор всегда направлен прямо на солнце и cos 0 = 1 .

Для параболоцилиндрических коллекторов, вращающихся вокруг фиксированной оси, параллельной оси Земли (т.е. полярной оси), показанной угол падения равен угловому положению Солнца в солнечный полдень относительно плоскости экватора (т.е. склонению - 5 ): cos 0 = cos 5 .

Среднегодовое значение cos 5 можно принять за 0,96 или склонение 5 можно рассчитать по приближенной формуле Купера [4]:

5 = 23,45 • sin

360 ^

где: n - порядковый номер дня года.

Для параболоцилиндрических коллекторов, вращающихся вокруг фиксированной горизонтальной оси восток-запад косинус угла падения определяется выражением [3]:

cos 0 = ( 1 - cos² 5 • sin² у )  ,               (6)

где:  У - часовой угол, равный нулю в солнечный полдень; каждый час соответствует 15° долготы.

Для параболоцилиндрических коллекторов, вращающихся вокруг фиксированной горизонтальной оси север-юг с непрерывной корректировкой, косинус угла определяется выражением [13]:

cos 0 = [(

]

sin ^ • sin 8 + cos^ • cos^ • cos®)2 + cos2 8 • sin2 ®

1/2

где: ^ - широта местности.

Влияние угла падения на оптическую эффективность параболоцилиндрического коллектора может быть записано в общем виде следующей функцией [4]:

F ( 0 ) — ( 1 - Atg ® ) cos 0 ,                     (8)

где: Atg0 - выражает уменьшение эффективной площади зеркальной поверхности, обусловленной концевыми эффектами, т.е. затенением торцевых конструкций концентратора;

A - геометрический коэффициент, определяемый исходя из конструктивных особенностей коллектора.

Величину геометрического коэффициента А можно вычислить с помощью следующего соотношения [4]:

B(f + C)+ F - Fc

A —

F З

,

Таким образом, если известны оптические коэффициенты коллектора, то для оценки оптических потерь коллектора можно записать следующее выражение:

QonT — Опад [1 - Сопт ' F (®)' F W1            (10)

С другой стороны, общее произведение измеренных и эмпирических оптических коэффициентов равно оптической эффективности системы.

П опт = С опт ' F ( ® ) ' F ( ф ),                  (11)

Оптическую эффективность параболоцилиндрического коллектора можно рассчитать, используя падающую на концентратор и поглощенную в приемнике солнечную энергию.

^П ОПТ = Q_nor / ^Q ПАД , 02)

Поглощенная энергия, приемником используя оптические коэффициенты, определяется по формуле [4]:

О П г = Е о ■ F 3 ■ С о_Пт • F ( © ) • F ф (13)

В целом, по формулам (10) и (11) могут быть рассчитаны оптические потери и эффективность параболоцилиндрического коллектора. В настоящее время практически достигнутая оптическая эффективность П _ОПТ солнечных параболоцилиндрических коллекторов лежит в диапазоне от 0,6 до 0,8.

Основными характеристиками, которые определяют эффек -тивность приемника, являются геометрическая форма, размеры, спектральные характеристики прозрачной изоляции и поглощающей поверхности, а также параметры теплового режима (рабочая температура, коэффициенты тепловых потерь, полученное полезное тепло и др.)

Геометрическая форма и размеры приемника. Как отмечалось выше, приемники параболоцилиндрических установок могут иметь различную геометрическую форму и размеры. Кроме того, установлено, что относительная концентрация отражателя зависит от формы и размеров приемника. Приведенный выше аналитический расчет параболоцилиндрических концентраторов с приемником разной формы показывает, что геометрическая концентрация К Г параболоцилиндрического концентратора с приемником в форме цилиндрической трубы равна 34,2 n , а с плоским приемником — 107,3 n , где n — отношение апертуры к фокальному расстоянию параболы.

Несмотря на разнообразие форм и существование оптимума в виде эллиптического цилиндра наибольшее применение нашли параболоцилиндрические концентраторы с приемниками, изготов -ленными из обычной цилиндрической трубы. Они удобны в эксплуатации, выпускаются промышленностью и путем несложных преобразований легко преобразуются в приемники солнечного излучения.

Важной характеристикой приемника являются также геометрические размеры: ширина или диаметр, толщина стенки и длина. Применение малой ширины или диаметра приемника требует повышения точности изготовления отражателя, что приводит к существенному увеличению КПД системы, однако в этом случае увеличивается и стоимость отражателя. Снижение точности концентратора приводит к повышению оптических потерь, т. е. значительная часть отраженной радиации проходит мимо трубы меньшего диаметра, и потери вследствие фактора формы (улавливание энергии приемником) могут достигать 30% и более [19]. При использовании большого диаметра приемника почти вся зеркально отраженная радиация улавливается трубой, и потери, вызванные наличием фактора формы, играют сравнительно малую роль (что составляет ® 10%). Однако при этом увеличиваются тепловые потери (конвективные и лучистые) с поверхности приемника, особенно при более высоких рабочих температурах. Применение прозрачной изоляции и селективных покрытий существенно уменьшает конвективные и лучистые потери тепла, что одновременно приводит к увеличению оптических потерь.

Таким образом, при невысоких рабочих температурах приемника (80^150°С) КПД параболоцилиндрической установки будет выше, чем КПД установки с малым приемником лишь в том случае, если рабочая температура будет 150: 180°С и тепловые потери для трубы меньшего диаметра начнут компенсировать влияние худшего фактора формы. Отсюда вытекает вопрос об оптимальном диаметре приемника для данного отражателя. В общем случае оптимальный размер приемника, обеспечивающий максимум полезной энергии, подбирается путем минимизации суммы оптических и тепловых потерь. Для идеального зеркала геометрические размеры приемника bид или dид (ширина или диаметр) могут быть определены по формуле

Ь ид = d ид = ^2Rtg1⁶'              (14)

cos »

где R — радиус зеркала. Он определяется следующим образом: R =    ^2>                            (15)

1 + cos »

Величина R меняется от R = f до R = Rmах при изменении угла охвата а от 0 до amax, и размер изображения увеличивается от bR=f = 2fig16 до bR = Rmax = 2Rmax X tg^'/cos»^ . Поэтому размер приемника определяется по bR = bmax , т. е. по конечным размерам фокального изображения.

Для реального зеркала геометрические размеры приемника могут быть определены по действительному значению Ф (ps + рс + ри = 45':2°) [2] или по наглядному примеру, приведенному на рис. 1.

Толщина стенки стальной трубы приемника обычно определяется по его рабочей температуре, т. е. по внутреннему давлению, и может быть рассчитана по формуле, взятой непосредственно из инструкции для котлов под давлением [3]:

S T = 1,1

d P /986

2 P ( 986 + 1 )

+ 0,013 d T

где Р — давление, кг/см² .

При использовании вакуумированной прозрачной оболочки в качестве тепловой изоляции приемника геометрические размеры стеклянной трубки можно определить по формулам [3].

d c = 2 d_T ,                                (17)

S T = 0,016 d_c ,                            (18)

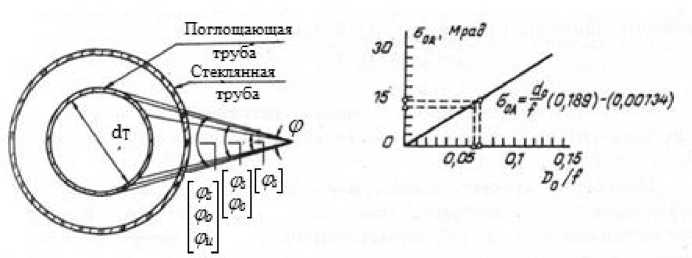
Рис. 1 Размерный анализ теплоприемника: ( ф _S -угловой радиус

Солнца; ф _с   — ошибка слежения; ф _и — ошибка изготовления ,

^ cA = y ^a s + ^ _c + ^ n + & R —среднеквадратичная точность установки

Уравнение (17) показывает, что диаметр стеклянной трубы d _c равен двойному диаметру стальной трубки d T . Уравнение (18) было получено исходя из разрушающего давления стеклянных труб в соответствии с формулой А. Е. Н. Lоуе [3].

На практике для трубчатых приемников параболоцилиндрических установок в качестве прозрачно-тепловой изоляции чаще всего используют трубы из стекла марки "Пирекс" или цилиндры из молибденового, боросиликатного стекла марки С49+С54 [4]. Эти стекла обладают хорошими оптическими качествами. Интегральное пропускание их в области длин волн солнечного излучения достаточно высоко — около 0,9^0,92, а поглощение и отражение минимальны — около А S=R S=0,025^0,07. В то же время стекла, являясь непрозрачными для длинноволнового излучения, выдерживают температурные перепады вплоть до 250°С [4].

Спектральные характеристики прозрачной изоляции могут быть изменены путем специальных обработок стекла — просветлением. При этом должны быть соблюдены следующие условия нанесения просветляющей пленки [4]:

8 = ( 2 m + 1 ) 2 /4 n , (19) ⁿ = n T ^

где 5 — толщина пленки; X — длина волны света; n _ст — показатель преломления стекла; n — показатель преломления пленки; m =0, 1, 2, 3; и т.д.

Нанесение просветляющих покрытий на стекло можно вести осаждением из раствора, испарением в вакууме, катодным распылением и т. д. Образующаяся на стекле пленка может состоять из фтористого магния, двуокиси кремния, двуокиси титана и т. д. В последнее время разработаны способы многослойного покрытия, который обеспечивает особо эффективное просветление. Применение таких покрытий дает не только высокое пропускание света в широкой области спектра, но и резко уменьшает долю рассеянного. Однако обработка поверхности стекла путем химического травления является наиболее простой и технологичной. При этом пропускательная способность стекла т _с высокого качества может быть увеличена до 0,94 ^ 0,95 при снижении отражательной способности R C до 0,02.

Проделанные расчёты позволяют систематизировать большое количество вариантов конструкции, выявить конструктивные и технологические достоинства и недостатки каждой из основных элементов параболоцилиндрической системы, а также сравнительно оценить их энергетические и технико-экономические характеристики.

На основе анализа научных исследований установлено что, успехи в области разработок стационарных параболоцилиндрических установок различного назначения еще очень скромные, однако, они уже применяются индивидуальными потребителями, так как конструкционно просты и экономически эффективны.