Расчет оптимальных упругодемпфирующих параметров шины как звена силовой передачи трактора

стабильном, и значит, выгодном режиме, а динамические процессы, потребляющие дополнительную энергию, в звеньях агрегата будут сведены к минимуму.

Среди разных способов решения задачи: установка в силовой передаче, в том числе и на оси ведущих колес трактора специальных упругодемпфирующих механизмов, может быть предложен следующий вариант. Суть его для колесного трактора заключается в использовании основного свойства пневматических шин, ради которого они и созданы - способности их к деформированию под действием приложенных к ним сил. Это приобретает особое значение и в связи с тем, что шина является замыкающим звеном при реализации силы тяги от преобразованного силовой передачей момента двигателя и одновременно звеном, прежде всего воспринимающим внешнее воздействие от рабочих органов машины-орудия. Цель работы и заключается в обосновании упругодемпфирующих свойств шины, при которых энергия колебательных процессов будет минимальной.

Это может быть при таком качестве переходных колебательных процессов, когда их затухание происходит по оптимальному закону. Для решения поставленной задачи воспользуемся интегральной квадратичной оценкой переходных процессов I 0 [2]:

м

I о = J x 2 (t)dt, о где x(t) - импульсная переходная функция.

Необходимо установить те свойства шины, при которых I 0 минимально.

Схема сил и моментов, действующих на ведущее колесо с шиной при неравномерном движении по горизонтальному опорному основанию представлена на рисунке 1.

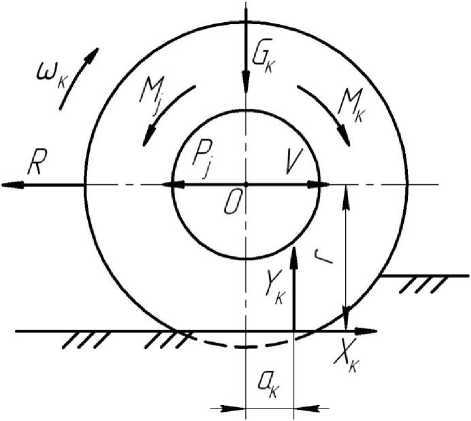
Рисунок 1 - Схема сил и моментов, действующих на ведущее колесо с шиной при неравномерном движении по горизонтальному опорному основанию

На схеме Mк - крутящий момент на оси ведущего колеса; Xк - реактивная, толкающая сила, возникающая в пятне контакта ведущего колеса с почвой [1]; R - сила сопротивления движению, учитывающая технологическое сопротивление рабочей машины-орудия и сопротивление качению ведомых колес трактора, преодолеваемая одним ведущим колесом; Gк - сила тяжести от массы, приходящейся на ось колеса; Yк - вертикальная составляющая реакции опорного основания; ак -плечо действия; г - силовой радиус колеса с достаточной точностью равный радиусу качения в свободном режиме [3]; Pj - сила инерции поступательной массы агрегата, приходящаяся на одно ведущее колесо; Mj - инерциальный момент на ведущем колесе.

Шина с продольной жесткостью с и демпфированием а воспринимает крутящий момент ведущего колеса Mк и в результате реализует при взаимодействии с почвенным опорным основанием толкающую силу Xк = с Л + аЛ, где 2 - ее продольная деформация. Реакция Yк на плече ак дает момент сопротивления качению Mf = Yк а к. Тогда шина как звено динамической системы колесо-шина-почва-остов машины будет представлена в дифференциальных уравнениях системы следующим образом:

I _к ю к + ( аЛ+ с Л ) г = M _к - M _f ,

•

< V - ю _к г + Л+ в = 0,                 (1)

•        •

mV - (аЛ+ сЛ) = - R, где Iк и Mf - моменты инерции и сопротивления качению ведущего колеса; m - масса агрегата, приходящаяся на одно ведущее колесо; V - скорость движения колеса; в - экспериментальный коэффициент, учитывающий буксование колеса.

В уравнениях системы (1), полученных по методике МАДИ [4], рассматриваются равновесие моментов и сил и кинематические связи, дополненные составляющей от буксования колеса на почве.

После преобразования Лапласа уравнения примут вид:

I к р Ю к ( Р ) + г( а р + с) Л (р ) = M ( р );

V (р) - гЮк (р) + (р + в)Л(р) = 0; mpV (р) - (ар + с)Л(р) = R(р), и, следовательно, передаточные функции от внешних для шины воздействий M и R для соответствующих показателей V и юк будут равны:

где

и w ^

( р ) = ™, А ( р )

W M ( р ) =

B ( р ) A ( р )

	I к р ( а р + с ) г	0
A ( р ) =	- г р + в	1	=
	0    - ( а р + с )	mp

= р ( а ₂ р ² + а 1 р + а ₀);

I к р  (ар + с ) г  1

B ( р ) = - г    р + в 0

0   - ( ар + с ) 0

0 ( ар + с ) г

0 р + в

1 - ( ар + с )

¹ =^ р ⁺ b 0

mp

Таким образом     W M ( p ) = W ^ ^K ( p ),    что

свидетельствует о равноценном прох о ж дени и че ре з звено «шина» воздействий и от с и л ов ой пе ре да ч и M , и от рабочей машины R . Один и з полюс ов передаточных ф у нк ци й, ра в ный н у л ю , когда остальные, безуслов но , я в л я ютс я отр ицате л ь ным и или вещественная часть их отрицательная, показывает, что по отношению к с кор ос ти дв и ж ени я агрегата или к угловой скорости оси колеса

рассматриваемая система неаси м пто тиче ски устойчива. То е с ть при пе ре х оде на нов ы й уров ень M или R система приобретает новые равнове с н ые

реализации предлагаемых значений c и α показывают результаты исследований в работе [5]. Произведено сравнение двух вариантов шин ведущих колес трактора: серийных радиальной конструкции 16,9R30 и опытных того же размера, но диагональнопараллельного строения оболочки. У первого варианта c =880 кН/м, α =2,06 кН·с/м, у второго c =1200 кН/м, α =14,42 кН·с/м. Оказалось, что величины спектральных плотностей колебательного процесса изменения скорости движения агрегата существенно различаются между собой при указанных вариантах (рисунок 2).

значения, отличные от прежних.

Согласно уравнениям (2) и формуле для

определения и нтегра л ь ной кв а дра т ично й переходных процессов [2] получим:

оцен ки

I

0 T 2

2 a

b 0 ^A 1 ⁺ b l ^A 2

^^^^^^s

0 V

^A 0

2 b 0 b 1

,

где A 0 =

a ₀ 0

^^^^^^s

a ₂

a ₁

; ^A 1 =

Следовательно

I 0 = 9 2

2 a ₀ ²

a ₁

a ₀

b ₀²( a ₀ a ₂

^^^^^^s

a ₂

a ₁

;

A

■ 2 =

a ₀ 0

a ₁

a ₀

.

2   22

+ a 1 ) + b 1 a 0

s

a ₀ a ₁

2 b 0 b 1

.

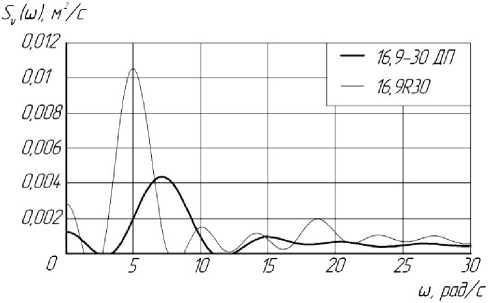
Рисунок 2 – Спектральные плотности процесса изменения скорости движения агрегата

Приравнивая нулю частную производную I₀ по a 1

содержит искомый параметр α)

22  2

d I 0      1 b 0 b 0 a 2 ⁺ b l a 0

--=------ d a 1     2 a 02 V a ₀ a 1 ²

и

учитывая зависимости

(3) и (4),

после

соответствующих преобразований запишем:

а = —

' C_ _ I к mP v в I к + mr 2

Таким образом, формула (5) показывает оптимальное соотношение коэффициентов продольного демпфирования α и продольной жесткости c шины, при котором колебательные процессы в рассматриваемой динамической системе будут сопровождаться минимальными потерями

энергии тракторного двигателя.

Решение поставленной задачи выполним на

конкретном примере машинно-тракторного агрегата, который состоит из трактора типа МТЗ-80 и культиватора или зерновой сеялки. Параметры агрегата, соотнесенные с одним ведущим колесом трактора известны: I _к =60 кг·м ² ; m =1400 кг; r =0,72 м; β =25 [5]. Значением коэффициента продольной жесткости шины c следует задаться, исходя из допустимой по соображениям ресурса величины деформации шины в этом направлении. Она не должна превышать 10 % от прогиба шины в радиальном направлении. Для шины размера 16,9R30, прогиб которой ограничен 85 - 90 мм, максимальная продольная деформация составляет 9 мм, что означает реализацию необходимой силы тяги колеса 9 кН при c =1000 кН/м.

Вычисление оптимального коэффициента продольного демпфирования шины по формуле (5) дает результат α =18,66 кН·с/м. Возможность 138

Меньшая величина спектральной плотности соответствует варианту комплектования колес диагонально-параллельными шинами, что дает лучшее приближение к указанным оптимальным значениям α и c. То есть в этом случае частотная функция для средних значений квадратов амплитуд гармоник, на которые может быть разложен случайный процесс, свидетельствует о меньшей интенсивности колебаний и, значит, лучшей энергетике функционирования агрегата. Обнаружена еще одна особенность . Ш ина, более отвечающая рекомендуемым упругодемпфирующим свойствам, является еще и своеобразным гасителем колебаний внешнего на агрегат воздействия [5].

Таким образом, разработанная математическая модель динамической системы колесо-шина-почва-остов машины позволяет рассчитать оптимальные параметры упругодемпфирующих свойств шины как звена силовой передачи трактора. Реализация этих параметров может быть осуществлена на основе конструкции шины с диагонально-параллельным строением оболочки. Ш ина приобретает свойства своеобразного гасителя колебаний, что способствует снижению энергозатрат при работе машиннотракторного агрегата.