Расчет ортотропных конструкций вариационным методом на основе трехмерных функций с конечными носителями
Автор: Хайруллин Ф.С., Сахбиев О.М.
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
В настоящее время для расчета сложных ортотропных тонкостенных конструкций, в том числе тонкостенных ортотропных оболочек, часто используется метод конечных элементов (МКЭ). Обычно при расчете этим методом применяется один из двух подходов: в первом подходе используется упрощающая гипотеза (например, гипотеза Тимошенко), в которой пренебрегают распределением напряжений вдоль толщины тонкостенной конструкции, что снижает размерность задачи; во втором подходе используются соотношения трехмерной теории упругости без использования упрощающих гипотез. В представляемом методе, который очень похож на МКЭ, при расчете также используются соотношения трехмерной теории упругости без упрощающих гипотез. В более ранней работе авторов был представлен вариационный метод определения напряженно-деформированного состояния трехмерных упругих конструкций, основанный на использовании аппроксимирующих функций с конечными носителями произвольной степени аппроксимации. В данной работе предложенные трехмерные аппроксимирующие функции используются для расчета ортотропных конструкций. Аналогичные аппроксимирующие функции для расчета оболочек использовались в работах, в которых разрешающие уравнения получались на основании упрощающей гипотезы. В общем виде метод основывается на использовании криволинейной системы координат, что делает его достаточно универсальным. Показано, что одни и те же аппроксимации могут быть использованы как для расчета трехмерных ортотропных конструкций, так и ортотропных оболочек. Отмечается, что расчет можно эффективно производить не за счет сгущения сетки, а за счет повышения порядка аппроксимирующих функций. Достоверность предложенного метода подтверждается представленными численными результатами, которые хорошо согласуются с известными решениями.
Трехмерные конструкции, вариационный метод, напряженное состояние, аппроксимация, расчет ортотропных конструкций
Короткий адрес: https://sciup.org/146211674
IDR: 146211674 | УДК: 539.3 | DOI: 10.15593/perm.mech/2017.2.11
Текст научной статьи Расчет ортотропных конструкций вариационным методом на основе трехмерных функций с конечными носителями
PNRPU MECHANICS BULLETIN
В современной технике использование композиционных материалов является экономически и технологически обоснованным. Одной из важных задач в механике композитов является расчет на прочность ортотропных конструкций.
В решении этих задач широкое распространение получил численный метод конечных элементов (МКЭ), основанный на различных формулировках. Большинством авторов МКЭ формулируется в виде метода перемещений [1–11]. Решения МКЭ для изотропных тел достаточно легко модифицируются и используются для ортотропных тел [4].
Одним из преимуществ данной формулировки является простота и, соответственно, удобство реализации. Метод, представленный в данной работе, во многом похож на МКЭ в виде метода перемещений. Отличия состоят в том, что многие неизвестные коэффициенты в аппроксимации не имеют физического смысла, точность решения достигается не за счет сгущения сетки, а за счет повышения порядка аппроксимации.
МКЭ в смешанных формулировках [12–16] также интенсивно развивается, поскольку имеет свои преимущества. К числу таких преимуществ можно отнести непрерывное поле напряжений, снижение порядка аппроксимирующих функций и т.п. При смешанной формулировке МКЭ узловыми неизвестными конечных элементов являются перемещения, напряжения или усилия.
Объемные конечные элементы на основе соотношений теории упругости без дополнительных гипотез о деформировании нормали использованы в работах [17–19]. В мето- де, который представлен в данной работе, также используются объемные конечные элементы трехмерной теории упругости.
Кроме того, можно отметить следующие методы расчета ортотропных конструкций. Например, в работе [20] предложен алгоритм, основанный на методе Ритца и методе продолжения решения по наилучшему параметру, который позволяет исследовать напряжен-но-деформируемое состояние (НДС) оболочек из ортотропных материалов. В [21] предлагается специально разработанный метод конструктивной анизотропии, который также основан на методе Ритца. В работе [22] для расчета ортотропных оболочек предложен численно-аналитический метод, основанный на методе разделения переменных (Фурье) в уравнениях с частными производными. В работах [23-26] развиваются численноаналитические методы расчета НДС ортотропных оболочек.
Ниже представлен новый численный метод решения пространственной задачи теории упругости для ортотропных конструкций с помощью конечно-элементных аппроксимаций произвольной степени. Основным преимуществом представленного метода по сравнению с традиционными вариантами МКЭ является то, что при повышении порядка аппроксимации не требуется увеличения количества узловых точек и использования в качестве узловых значений производных от искомых функций, тем более производных высоких порядков.
В данной работе результаты, полученные представленным методом, анализируются и сопоставляются с результатами других авторов [23, 27].
1. Методика моделирования
Вводятся глобальная система координат x , y , z и ортогональная криволинейная система координат а 1 , а 2, а 3 (рис. 1), в которой задаются определяющие уравнения деформации упругого тела. Предполагается, что перемещения и деформации малы, справедлив закон Гука. В зависимости от формы рассматриваемой конструкции выбирается соответствующая система координат аи а 2, а 3: декартова, цилиндрическая, сферическая и т.п.
В криволинейной системе координат а 1 , а 2, а 3 деформации определяются через компоненты перемещения по формулам [28]
1 5 U
'А , + kJ kA ,
Ai да i у.. = 2s
1 j У
1 5 U 1 5 U, ,
-- +-- j - U,
A j 5а j A 5а ,
-
kU ,
i = 1,3,
где un u 2, u 3 - компоненты перемещения произвольной точки тела в системе координат av a 2, a 3; A i - коэффициенты Ляме; kjj - кривизна кривой а i в плоскости а i а j (главные кривизны); у 12, у 23, у 31 - углы сдвига; индексы j , l получаются круговой перестановкой индексов i , j , l .
Физические соотношения для ортотропного материала записываются так:
И=[ E ]{е}.
Пусть оси координат а 1 , а 2, а 3 совпадают с направлениями ортотропии (направления упругой симметрии). Матрица упругости в этом случае примет вид [29]
|
" E 11 , |
E 12 , |
E 13 , |
0, |
0, |
0 " |
|
|
E 21 , |
E 22 , |
E 23 , |
0, |
0, |
0 |
|
|
[ E ] =A |
E 31 , 0, |
E 32 , 0, |
E 33 , 0, A |
0, " G 12 , |
0, 0, |
0 0 |
|
0, |
0, |
0, |
0, |
A" G 23 , |
0 |
|
|
_ o, |
0, |
0, |
0, |
0, |
A" G 31 _ |
|
|
где E 11 = E 1 (1 - v 23 " v 32 ); E 22 |
= E 2(1 |
-V 31 |
V 13 ); E 33 _ |
E 3(1 |
-V 12 "V 21 ) |
; |
E 12 E 21 E 2( V 12 + V 13 "V 32 ); E 13 E 31 E 2 ( V 13 + V 12 "V 23 );
E 23 = E 32 = E 3 ( V 23 + V 21 " V 13 );
A = 1 - V 12 " V 21 - V 23 " V 32 - V 31 " V 13 - 2 " V 12 " V 23 " V 31 •
Здесь E 1, E 2, E 3 – модули упругости в соответствующих направлениях; G 12, G 23 , G 31 – модули сдвига соответственно в плоскостях ( а 1 а 2), ( а 2 а 3), ( а 3 а 1 ); v ij - коэффициенты Пуассона, для которых должны выполняться равенства
E
V 21 = ^Т V 12 ; V 32
E
E
= - V
E 2
23 ; V 13
E
1 V E 3
Исследуемая трехмерная конструкция разбивается на подобласти в виде криволинейных шестигранников Vk (рис. 1), грани которых являются кусочно-гладкими поверхностями и описываются в криволинейной системе координат а 1 , а 2, а 3 уравнениями а 3 = F 1 ( a 1 , а 2), а 3 = F 2( a 1 , а 2), а 2 = F 3( a 3, а 1 ), а 2 = F 4 ( a 3, а 1 ), а 1 = F 5 ( a 2, а 3), а 1 = F 6 ( a 2, а 3), где F i , i = 1,6 - однозначные функции класса C 1.
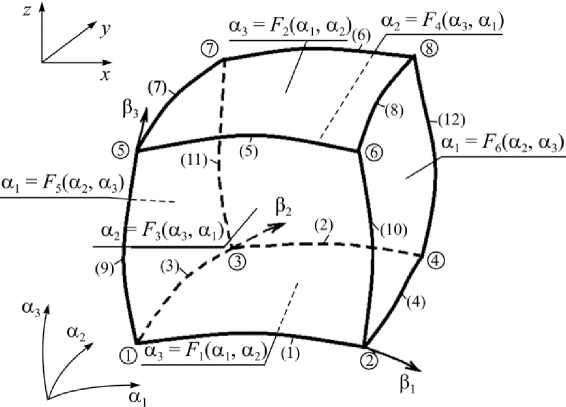
Рис. 1. Подобласть V k в виде криволинейного шестигранника
Fig. 1. Subarea V k in the form of a curvilinear hexagon
В подобласти Vk вводится дополнительная криволинейная система координат Р 1, Р 2, Р 3 , которая связана с системой координат a 1, a 2, а 3 следующим образом:
а1 = F5 ( а25, a 35 )( 1 — Р1 ) + F6 ( a 26 , a36 ) Р1 + a10, a2 F3 ( a33 , ai3 )( 1 Р2 ) + F4 ( a34, ai4 ) Р2 + a20, (4)
a 3 = F ( ail, a 21 ) ( 1 - P3 ) + F2 ( a12, a 22 ) P3 + a 30, где функции a25 = a25 (P2,P3), a35 = a35 (P2,P3), a10 = a10 (P1,P2,p3) и т.д. подбираются таким образом [1], что на гранях Qk, i = 1,6 подобласти Vk уравнения (3) переходят в уравнения этих граней, на граничных линиях X', j = 1,12 - в уравнения этих линий; 0 <Р1, Р2, Р3 < 1.
Для определения напряженно-деформированного состояния конструкции используется вариационный принцип Лагранжа [30], на основании которого должно выполняться условие
KK se = £а Ek (и )=£/(аи к-а Wk) d a=о, (5)
к = 1 к = 1 Q
Q к где Е - полная энергия конструкции; Ек - полная энергия подобласти Vk; Пк, S Wk -удельная потенциальная энергия деформации и вариация работы внешних сил единицы объема подобласти Vk ; K– количество подобластей.
В подобласти Vk компоненты перемещения U = { м 1 , u 2 , u 2 } T аппроксимируются функциями, заданными в локальной криволинейной системе координат 3 1 , Р 2, Р 3, следующим образом:
NML
U i = ZZZ D^t n ( Р 1 ) t , ( р 2 ) t, ( Р э ) , (6)
n = 1 m = 1 l = 1
здесь Diknml – неизвестные постоянные; функции формы t (P1) = 1 -P1,12 (P1) = P1, t, (P1) = t, (P,) [12 (P1)]m-2 (m = 3M).
Аппроксимирующие функции (6) подставляются в соотношения (1), а затем в физические соотношения для ортотропного тела (2). Используя известные соотношения для потенциальной энергии деформации, на основании вариационного уравнения (5) получается система уравнений для определения неизвестных постоянных Diknml .
2. Результаты расчетов
Для проверки предложенного метода была рассмотрена задача об изгибе трехслойной балки из углепластика под действием синусоидальной нагрузки (рис. 2). В качестве системы координат a1, a2, a3 была использована декартова система координат. В работе [27] для этой задачи приводится аналитическое решение теории упругости, решение задачи на основе теории оболочек типа Тимошенко, решение задачи на основе классической теории оболочек и решение автора методом конечных элементов на основе смешаного функционала с независимой аппроксимацией напряжений и перемещений в каждом слое. Автор половину балки разбивал на восемь трехслойных конечных элементов, которые удовлетворяют гипотезе Тимошенко.
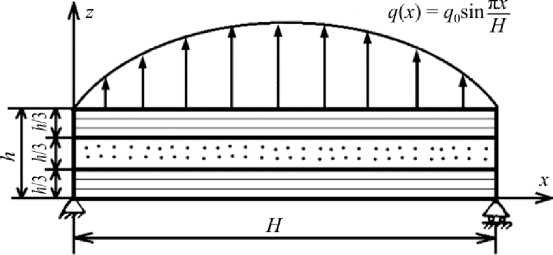
Рис. 2. Трехслойная балка из углепластика под действием синусоидальной нагрузки
Fig. 2. Three-layer beam made from a coal plastic under the influence of sinusoidal loading
Балка состоит из углепластиковых однонаправленно армированных монослоев со следующими характеристиками (ось 1 совпадает с направлением армирования): E11 = 1,724 - 10 5 МПа, E 22 = 6895 МПа, G 12 = G31 = 3448 МПа, G 23 = 1379МПа, v 12 = 0,25. Направления армирования 1-го и 3-го слоев совпадают с осью балки x , а направление армирования 2-го слоя перпендикулярно оси балки. Для первого и третьего слоев Exx = E 11, Eyy = E 22 , Gxy = Gxz = G 12 , G yz = G 23 , Для второго слоя Exx = E 22 , Eyy = E 11 , Gxz = G 23 . Приняты следующие численные параметры: H = 24 м, b = 1 м, h = 2,4 м, q 0 = 0,6895 МПа.
При расчете балка разбивалась на четыре конечных элемента: по одному элементу на верхний и нижний слои и два элемента по толщине среднего слоя. Порядок аппроксимации задавался следующими константами в выражении (6): M = N = L = 7 .
Для сравнения результатов были введены следующие безразмерные величины:
а
xx
q 0
а xz
о _ 100 E, -• h 3 x-^ ; w =----22—— w.
q 0 q 0 • H
В таблице приводятся безразмерный прогиб w в сечении x = Н /2 и погрешность а в % по отношению к решению теории упругости.
Безразмерный прогиб w в сечении x = Н /2 и погрешность а в % по отношению к решению теории упругости Dimensionless deflection w in the cross section x = Н /2 and an error a in % in relation to the solution of the theory of elasticity
|
Прогиб в центре балки |
Аналитическое решение [27] |
МКЭ [27] |
Решение по представленной методике |
||
|
Теория уругости |
Классическая теория |
Теория Тимошенко |
|||
|
w |
0,93164 |
0,50966 |
0,7631 |
0,9886 |
0,9441 |
|
а |
– |
45,29 |
18,09 |
–6,11 |
–1,33 |
Из таблицы видно, что схема разбиения на четыре конечных элемента и использованный порядок аппроксимации оказались достаточными для получения решения с погрешностью 1,33 %.
На рис. 3 приводится безразмерное напряжение σ xx в сечении x = Н /2, на рис. 4 – безразмерное напряжение σ xz в сечении x = 0 . На этих рисунках сплошной линией приведены данные согласно представленной методике, остальные графики соответствуют данным работы [27].
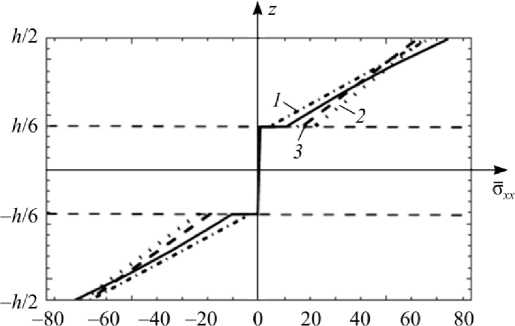
Рис. 3. Безразмерное напряжение σ xx в сечении x = H /2: кривая 1 – решение теории упругости [27]; кривая 2 – решение МКЭ [27] и кривая 3 – решение по классической теории слоистых балок [27] Fig. 3. The dimensionless stress σ xx in the cross section x = H /2.
Сurve ( 1 ) shows the solution based on the theory of elasticity [27], curve ( 2 ) shows the solution based on the FEM [27] and curve ( 3 ) shows the solution based on the classical theory of layered beams [27]
Как видно из таблицы и рисунков, полученное решение очень близко к решению теории упругости.
В следующем примере рассмотрена задача о расчете на прочность однослойной шарнирно-закрепленной ортотропной оболочки (рис. 5). В качестве системы координат α 1 , α 2 , α 3 была использована цилиндрическая система координат, где глобальные координаты x , y , z связаны с координатами α 1 , α 2 , α 3 соотношениями x = α 1 ⋅ cos( α 2 ) ≡ r ⋅ cos( ϕ ), y =α 1 ⋅ sin( α 2 ) ≡ r ⋅ sin( ϕ ), z =α 3 ≡ z .
Коэффициенты Ляме и кривизны A 1 = 1; A 2 = a 1; A 3 = 1, k 21 = , остальные kij = 0.
a 1
На оболочку, имеющую внешний радиус R =1,60 м, длину H = 2,24 м, толщину h = = 0,006 м, действует нагрузка P = 1000 Н, которая равномерно распределена на элементе размером a ϕ × az , где a ϕ – длина дуги окружности, соответствующей углу ∆ϕ . Упругие постоянные имеют следующие значения: E = 4,65 104 МПа; E = E = 0,7 104 МПа; G = G = zz ϕϕ rr ϕ z r ϕ
= G zr = 0,7 10 4 МПа; ν zy = 0,25; ν r ϕ = ν zr = 0. Нагрузка приложена к элементу с размерами 0,0558 ×0,24 м, находящемуся на поверхности кольца, равноудаленного от торцов оболочки. В силу симметрии задачи рассматривалась одна четвертая часть оболочки (0 ≤ z ≤ H /2; 0 ≤ϕ≤π ), которая разбивалась на шесть конечных элементов. Порядок аппроксимации задавался следующими константами в выражении (6): M = N = L = 6 .
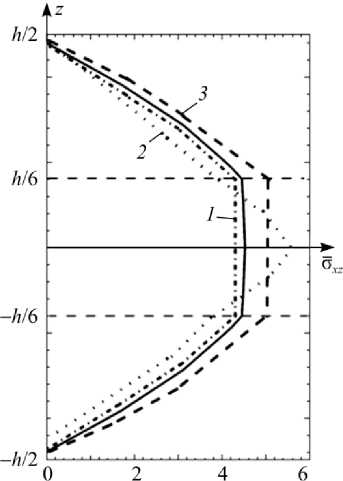
Рис. 4. Безразмерное напряжение о xz в сечении x = 0: кривая 1 – решение теории упругости [27]; кривая 2 – решение МКЭ [27] и кривая 3 – решение по классической теории слоистых балок [27]
Fig. 4. The dimension stress о xz in the cross section x = 0. Сurve ( 1 ) shows the solution based on the theory of elasticity [27], curve ( 2 ) shows the solution based on the FEM [27] and curve ( 3 ) shows the solution based on the classical theory of layered beams [27]
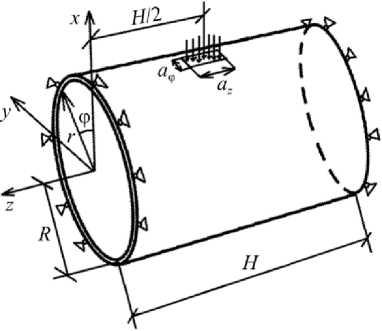
Рис. 5. Однослойная шарнирно-закрепленная (неподвижно) ортотропная оболочка под действием распределенной нагрузки Fig. 5. Single layer hinged-fixed (motionless) orthotropic shell under distributed loading
В статье [23] имеются результаты расчета данной оболочки. Эти результаты представлены на рис. 6, а и рис. 7 с целью сравнения с результатами, полученными по представленной методике.
На рис. 6, а изображено радиальное перемещение u r в сечении z = Н /2 в зависимости от окружной координаты φ: кривая 1 – решение с использованием методики
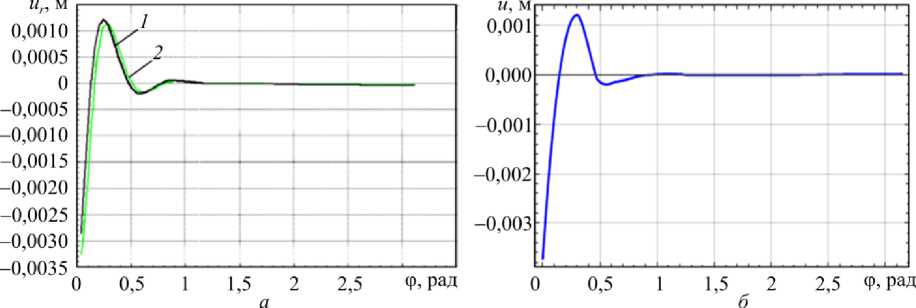
Рис. 6. Радиальное перемещение u r в сечении z = H /2, в зависимости от окружной координаты φ: а – решение с использованием методики автора [23] – кривая 1 , решение в пакете ANSYS – кривая 2 , б – представленная методика
Fig. 6. Radial movement u r in the cross section z = H /2 depending on the district coordinate φ, ( a ) is from the paper in [23], the solution with the use of the author’s technique is shown in curve ( 1 ), the solution using ANSYS package is in curve ( 2 ), ( b ) is the presented technique
автора, в котором решение искалось с помощью рядов Фурье со 130 гармониками, кривая 2 – решение, полученное с использованием пакета ANSYS с сеткой 17900 конечных элементов, полученных на основе теории оболочек.
На рис. 6, б приведено решение, которое получено на основании методики, изложенной в данной статье.
На рис. 8 приведено аналогичное решение, которое получено на основании методики, изложенной в данной статье.
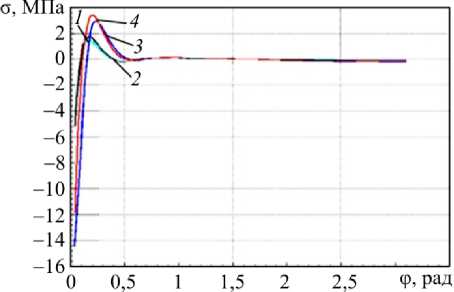
Рис. 7. Распределение продольного σ zz (кривые 1 , 3 ) и окружного σ ϕϕ (кривые 2 , 4 ) напряжений в сечении z = H /2 на внешней поверхности оболочки в зависимости от угловой координаты φ; кривые 1 , 2 – решение с использованием методики автора; 3 , 4 – решение с использованием ANSYS
Fig. 7. Distribution of the longitudinal σ zz (curves 1 , 3 ) and district σ ϕϕ (curves 2 , 4 ) stresses in the cross section z = H /2 on the external surface of the shell depending on the angular coordinate φ, curves 1 , 2 show the solution using the author’s technique, 3 , 4 show the solution using ANSYS
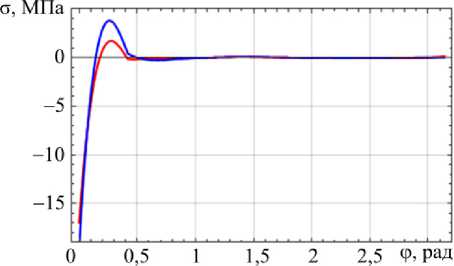
Рис. 8. Распределение продольного σ zz (синий цвет) и окружного σ ϕϕ (красный цвет) напряжений в сечении z = H /2 на внешней поверхности оболочки в зависимости от угловой координаты φ
Fig. 8. Distribution of the longitudinal σ zz (blue color) and district σ ϕϕ (red color) stresses in the cross section z = H /2 on the external surface of the shell depending on the angular coordinate φ
Как видно из рис. 6, 7, 8, характер распределения перемещений и напряжений и их величины даже при расчете на сетке из шести элементов вполне соответствуют данным работы [23], в которой приведено решение для 17900 конечных элементов. Общее число неизвестных в разрешающей системе уравнений по представленной методике составило 2552.
Заключение
Предложен метод определения напряженно-деформированного состояния ортотропных конструкций, основанный на объемном конечном элементе трехмерной теории упругости. Как показывают приведенные результаты представленный метод можно использовать для расчетов тонких ортотропных и многослойных оболочек без использования дополнительных гипотез о распределении напряжений по толщине оболочки. Данный метод может быть эффективно использован для расчета сложных ортотропных конструкций даже без использования густой сетки. Точность расчетов достигается высоким порядком аппроксимаций. Предложенный метод наиболее эффективен, когда сложная трехмерная конструкция может быть разбита на не очень большое количество шестигранников вида Vk . Если же для задания конструкции требуется большое количество подобных элементов или с помощью рассмотренных элементов описать данную конструкцию невозможно, то целесообразно использовать традиционные варианты МКЭ.
Список литературы Расчет ортотропных конструкций вариационным методом на основе трехмерных функций с конечными носителями
- Хайруллин Ф.С., Сахбиев О.М. О методе расчета трехмерных конструкций сложной формы//Вестн. Казан. техн. ун-та. -2014. -Т. 17, № 23. -С. 328-330.
- Хайруллин Ф.С. Вариационные методы расчета тонкостенных конструкций сложной формы на основе аппроксимирующих функций произвольного порядка с конечными носителями: дис. … д-ра физ.-мат. наук. -Казань: Изд-во Казан. гос. ун-та. -2007. -267 c.
- Хайруллин Ф.С. Моделирование напряженно-деформированного состояния тонких оболочек с вырождающейся областью//Изв. вузов. Авиационная техника. -Казань: Изд-во Казан. гос. техн. ун-та им. А.Н. Туполева, 2009. -№ 4. -С. 68-70.
- Голованов А.П., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций -М.: Физматлит. 2006. -392 с.
- Якупов Н.М., Галявиев Ш.Ш., Хисамов Р.З. Метод исследования напряженно-деформированного состояния конструкций сложной геометрии//Вестн. Рос. ун-та дружбы народов. Серия: Инженерные исследования. -2002. -№ 1. -С. 27-31.
- Бережной Д.В., Сагдатуллин М.К. Трехмерный конечный элемент для расчета оболочек средней толщины//Вестн. Казан. техн. ун-та. -2013. -Т. 16, № 9. -C. 256-261.
- Джабраилов А.Ш., Клочков Ю.В., Николаев А.П. Конечно-элементный расчет оболочек вращения с ветвящимся меридианом//Изв. вузов. Авиационная техника. -2009. -№ 1. -C. 15-19.
- Giamperi A., Perego U. An interface finite element for the simulation of localized membrane-bending deformation in shells//Comput. Meth. Appl. Mech. and Eng. -2011. -Vol. 200. -№ 29-32. -P. 2378-2396.
- Серпик И.Н. Эффективный конечно-элементный анализ плит Тимошенко с исключением заклинивания изгибных деформаций//Изв. вузов. Строительство. -2010. -№ 10. -C. 8-17.
- Мануйлов Г.А., Косицын С.Б., Бегичев М.М. Исследование устойчивости упругих пластин и оболочек при помощи конечно-элементного моделирования//Строит. мех. инж. конструкций и сооруж. -2011. -№ 1. -C. 58-65.
- Николаев А.П., Бандурин Н.Г. К расчету оболочек методом конечного элемента//Строительная механика и расчет сооружений. -1980. -Т. 5. -C. 21-25.
- Определение напряжений в зонах сочленения пластин с использованием конечных элементов различных конфигураций/А.П. Киселев, Н.А. Гуреева, Р.З. Киселева, В.В. Леонтьева//Инженерные системы -2015: тр. VIII Междунар. науч.-практ. конф./Рос. ун-т дружбы народов; под общ. ред. Н.К. Пономарева. -М., 2015. -C. 84-88.
- Гуреева Н.А. Анализ линейного и нелинейного деформирования тел в криволинейных координатах на основе смешанного метода конечных элементов: дис. … д-ра физ.-мат. наук. -Волгоград, 2016. -C. 381.
- Шайдуров В.В., Шуть С.В. Применение эрмитового биквадратного конечного элемента//Вестн. Сиб. гос. аэрокос. ун-та им. академика М.Ф. Решетнева. -2014. -№ 2 (54). -C. 80-85.
- Шлычков С.В. Методика расчета корпусных элементов музыкальных инструментов: дис.. канд. техн. наук -Йошкар-Ола, 2004. -170 c.
- Филиппович А.П. Расчет пологих оболочек при наличии концентраторов напряжений с помощью метода конечных элементов//Материалы Восьмой Всесоюз. конф. по современным проблемам дифференциальной геометрии. 20-21 сент. 1984 г. -Одесса, 1984. -С. 161.
- Hall K.J., Potirnche G.P. A tree-dimensional edge-crack finite -element for fracture mechanics applications//Int. J. Solids and Struct. -2012. -Vol. 49. -No. 2. -P. 328-337.
- Composite delimitation modeling using a multi-layered solid element/I. Tawk, P. Navarro, J.-F. Ferrero, J.-J. Barrau, E. Abdullah//Compos. Sci. and Technol. Англ. -2010. -Vol. 70. -No. 2. -P. 207-214.
- Trach Y., Burdekin F.M. A tree dimensional analysis of fracture mechanics test pieces of different geometries. Pt 1. Stress-state ahead of the crack tip//Int. J. Pressure Vessels and Pip. -2012. -No. 93-94. -P. 42-50.
- Семенов А.А. Геометрически нелинейная математическая модель расчета прочности и устойчивости ортотропных оболочечных конструкций: дис. … канд. техн. наук. -СПБ., 2014.
- Каменев И.В., Семенов А.А. Обоснование использования метода конструктивной анизотропии при расчете пологих оболочек двоякой кривизны, ослабленных вырезами//Вестник Пермского национального исследовательского политехнического университета. Механика. -2016. -№ 2. -С. 54-68.
- Виноградов Ю.И. Мультипликативный метод решения краевых задач теории оболочек//Прикладная математика и механика. -2013. -Т. 77, № 4. -С. 620-628.
- Емельянов И.Г., Кузнецов А.В. Применение виртуальных элементов при определении напряженного состояния оболочек вращения//Вычислительная механика сплошных сред. -2014. -Т. 7, № 3. -С. 245-252.
- Григоренко А.Я., Яремченко Н.П., Яремченко С.Н. Расчет напряжeнно-деформированного состояния слоистых прямоугольных в плане пологих ортотропных оболочек в уточнeнной постановке//Reports of the National Academy of Sciences of Ukraine. -2012. -№ 2.
- Нерубайло Б.В., Ольшанский В.П. Асимптотический метод расчета конической оболочки на действие локальной нагрузки//МТТ. -2007. -№ 3. -С. 115-124.
- Григоренко Я.М. Решение краевых задач о напряженном состоянии упругих тел сложной геометрии и структуры с применением дискретных рядов Фурье//Прикладная механика. -2009. -Т. 45, № 5. -С. 3-52.
- Рикардс Р.Б., Метод конечных элементов в теории оболочек и пластин. -Рига: Зинатне, 1988. -284 с.
- Новожилов В.В. Теория упругости. -Л.: Судпромгиз, 1958. -371 с.
- Алфутов Н.А., Зиновьев П.А., Попов Б.Г. Расчет многослойных пластин и оболочек из композиционных материалов. -М.: Машиностроение, 1984. -264 с.
- Абовский Н.П., Андреев Н.П., Деруга А.П. Вариационные принципы теории упругости и теории оболочек. -М.: Наука, 1978. -288 с.


