Расчет ослабляющих экранов щелевого типа в виде многоугольников
Автор: Батороев Анатолий Сократович, Ширеторов Игорь Дондупович
Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu
Рубрика: Физика
Статья в выпуске: 3, 2013 года.
Бесплатный доступ
Предложен метод расчета ослабляющих экранов в виде многоугольников, с помощью которого определены их оптимальные параметры, обеспечивающие локальное подавление помехового поля. Исследованы пространственно-частотные характеристики экранов.
Щелевой экран, ослабление, дифракция
Короткий адрес: https://sciup.org/148181804
IDR: 148181804 | УДК: 621.371:
Calculation of slot type attenuating screens in the form of polygons
A method of calculation of attenuating screens in the form of polygons has been presented; the optimal parameters providing local suppression of interference field have been defined with its help. The spatial and frequencies characteristics of these screens have been studied.
Текст научной статьи Расчет ослабляющих экранов щелевого типа в виде многоугольников
В практике использования защитных экранов известны щелевые экраны с прямыми прорезями [1], а также кольцевые и секторные экраны. Для ослабления помеховых полей также представляют интерес щелевые экраны в виде многоугольников, которые из-за своих ограниченных размеров должны иметь узконаправленные характеристики. В данной работе исследованы ослабляющие свойства щелевых экранов в виде правильных многоугольников (треугольника, квадрата и т.д.). Геометрия задачи представлена на рис. 1.
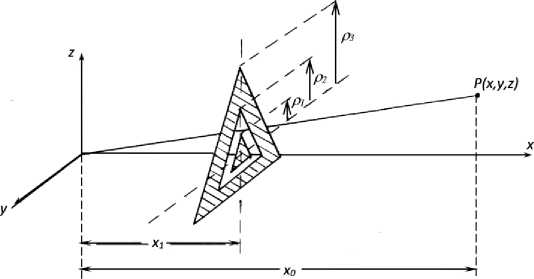
Рис. 1. Геометрия задачи
При минимизации помеховых полей в качестве целевой функции выбираем множитель дифракционного ослабления Ф. Тогда из условия абсолютной минимизации поля в «фокальной» точке, которой соответствуют координаты (x0, 00) и частота f 0, уравнение целевой функции запишется:
2 к +1 — / \
Ф = Е(" 1) j-1 • F (uy)= 0, j=1
где функция FU ) определяет множитель дифракционного ослабления на базовом экране с обобщенным параметром, определяющим его размеры в соответствии со следующим представлением:
и j- , j = 1, 2, -,2k + 1,
Uj b 1 ( x 0 )
p j - линейный размер соответствующего экрана (рис. 1), b1(x0) - радиус первой зоны Френеля в плоскости экрана относительно «фокальной» точки.
В случае щелевых экранов в виде правильных многоугольников, где базовым экраном служит правильный многоугольник, путем разбиения его на 2n прямоугольных треугольников, стягивающихся вершинами при острых углах к точке прохождения луча, которая является центром самого многоугольника, решение на основании [2] получается обычным суммированием опорных функций (решений на прямоугольных треугольниках):
F ( U j ) = 1 - 2 nf [ к = п , U j \ ’
где f к u j ) =У - 1 f 0 ( У u ) , 2 п 4
• п 2
i u 2 j
iu
/ х с 2 j z f0 V u^= — Е(-0к
П к = 0
k = 0
(п • u ,2) 2 к ( 4 к - 1)!
to
• C 2 к V ) - i ^И k ^
к = 0
2 2 к + 1
( п • U j ) , x
( 4 к + 1)! ^ C 2 k + 1 У )
Функция f ( T , U j ) определяет указанное решение на отверстии в виде прямоугольного треугольни-
V ка при прохождении луча через вершину при остром угле T. В формуле (4) Cv = 2 J sin 2v tdt, а 0
Френелевский параметр u j согласно формуле (2) соответствует гипотенузе прямоугольного треугольника p j .
В частном случае для правильного треугольника множитель ослабления вычисляется по формулам (3) и (4) при n = 3, T = п /3. Решение уравнения (1) с использованием соответствующих функций (3) для каждого вида экрана осуществлено на базе ранее разработанного метода годографа [1]. Полученные результаты представлены на рис. 2 для треугольного экрана (n = 3) с различным числом щелей k.
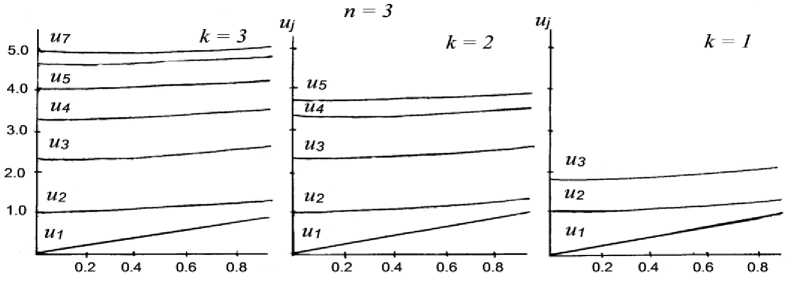
Рис. 2. Оптимальные параметры для треугольника экрана (n = 3) с различным числом щелей k
Однако найденная серия щелевых экранов с оптимальным размещением его составляющих элементов обеспечивает максимальное (локальное) подавление помехового поля в «фокальной» точке, а практический интерес имеют экраны, обеспечивающие эффективное подавление помехового поля в некотором пространстве вокруг «фокальной» точки, а также в некотором частотном диапазоне.
В отличие от экранов, описанных в [1], естественный интерес представляет исследование распределения дифракционного поля, создаваемого оптимизированными экранами ограниченных размеров в перпендикулярной к направлению распространения плоскости yz.
Методика расчета этого распределения сводится к расчету функции Ф по формулам (3) и (4) в произвольной точке пространства, определяемого координатами:
qy bl(x 0) v Am (1 - m)x 0 , zz z bl(x 0) V Am (1 - m)x 0
x m = —-
x
характеризующими смещение исследуемой точки от «фокальной». Этой точке в плоскости экрана соответствует точка стягивания вершин прямоугольных треугольников, полученных при соответствующих разбиениях. Причем эта точка смещена от центральной точки, соответствующей «фокальной» точке, как по вертикали, так и по горизонтали.
На рис. 3 представлены результаты расчета в виде линий постоянного уровня подавления, которые дают общую картину распределения дифракционного поля вокруг их наименьшего уровня в плоскости yz. Эти линии в случае экранов в виде правильных треугольников близки по форме к окружности .
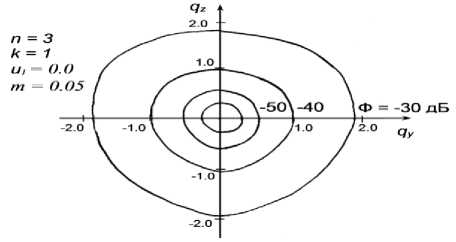
Рис. 3. Линии постоянного уровня подавления
Расчет частотных характеристик экранов можно осуществить путем введения параметра qf = (f – fo)/fo и вычисления Ф по формулам (3) и (4) с учетом этого параметра. На рис. 4 приведено сравнение частотных характеристик, создаваемых однощелевыми экранами в виде различных видов правильных многоугольников (n = 3, 4, 6), а также однокольцевыми экранами с u1=0,0. Частотный диапазон эффективного подавляющего действия шире у экранов в виде правильных треугольников по сравнению с остальными видами, а также по сравнению с кольцевым экраном.
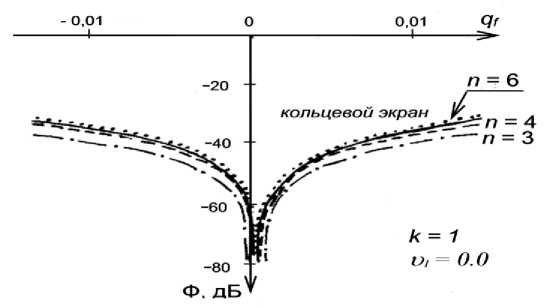
Рис. 4. Частотные характеристики однощелевых экранов для различных многоугольников (n = 3, 4, 6)
Для проверки теоретических расчетов проведены модельные измерения. Степень подавления помехового поля, обеспечиваемая синтезированными экранами, составила 30-40 дБ, что показывает эффективность выбранного метода исследования.
