Расчет отражателя, формирующего радиально-симметричную диаграмму направленности

Задача расчета зеркала, формирующего заданную диаграмму направленности (ДН) излучения, является актуальной при расчете систем освещения, фар автомобилей, устройств подсветки LCD-мониторов и т.д. Известны аналитические методы расчета радиальносимметричных зеркал для формирования заданных ДН при точечном источнике света [1-3]. Эти методы сводят задачу к решению дифференциального уравнения первого порядка с последующим интегрированием [13]. Методы [1-3] не учитывают возможные многократные отражения луча от зеркала.

В данной статье рассмотрен итерационный метод расчета радиально-симметричного зеркала из условия формирования заданной ДН при точечном источнике. В отличие от [1-3], представленный метод учитывает многократные переотражения лучей. Поверхность зеркала определяется в виде полинома. Коэффициенты полинома вычисляются из условия минимума функции невязки, представляющей различие расчетного и заданного распределений интенсивности. Для расчета интенсивности разработан алгоритм трассировки лучей с учетом многократных отражений.

2. Расчет диаграммы направленности от отражателя без учета многократных отражений

Пусть радиально-симметричное зеркало задано в виде r ( в ) (рис. 1). Точечный источник находится в

1 I 0 sin ( в ) d ^ = | I( а ) sin ( а ) dа|

где - I о интенсивность источника, в - угол, под

которым луч выходит из источника, а - угол, под которым луч выходит из апертуры отражателя. Под апертурой отражателя будем понимать круговую область, проходящую через крайние точки зеркала. Из (1) получим:

I ( а ) = I ₀( в ) sin ( в )/ ^f sin ( а ( в ) ) d ^ )          (2)

( х      ’ da)

Представление (2) неудобно для расчета, поскольку его нельзя использовать в области каустик. Воспользуемся интегральным представлением формулы (2):

I ^{( а} ) = J

I о ( в ) sin ( в ) sin ( а ( в ) )

5(а - а (в))dв

Аппроксимируем дельта функцию в (3) иглообразной функцией Гаусса:

I ( а ) = -1= J а ^п

I о ( в ) sin ( в ) sin ( а ( в ) )

( ^а - ^{а ( в} ) ) ² exp(----- 2— ^) d в ^,(4)

a ²

где a – параметр функции Гаусса.

В (4) неизвестна зависимость а ( в ). Данную зависимость найдем из закона отражения света [3]:

S 2 = S 1 - N ( N 1 ■ S 1 ),

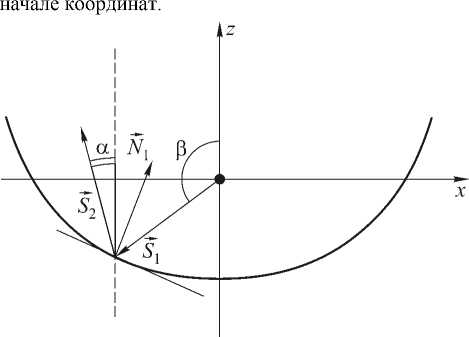
Рис. 1

Для расчета диаграммы направленности воспользуемся законом сохранения светового потока [1-3]:

где S₁ – вектор луча выходящего из источника, S₂ = ( s x , s z ) - вектор отраженного луча, N 1 - нормаль к поверхности зеркала в точке отражения.

Согласно (5), функция а ( в ) имеет вид:

α ( β ) =

2 π - arcsin( s_x ), при s_z ≥ 0 π + arcsin( s_x ), при s_z < 0.

• 3.    Расчет диаграммы направленности от зеркала с учетом многократных отражений

Если отраженный луч S₂ в (5) не попадает в апертуру зеркала, то происходит переотражение (рис. 2).

Для определения факта переотражения найдем координаты точки пересечения отраженного луча с направлением S2 с прямой, проходящей через крайние точки зеркала. Если координата x точки пересечения по модулю больше, чем модуль коор- динаты x крайней точки зеркала, то отраженный вектор не попадает в апертуру и происходит переот-

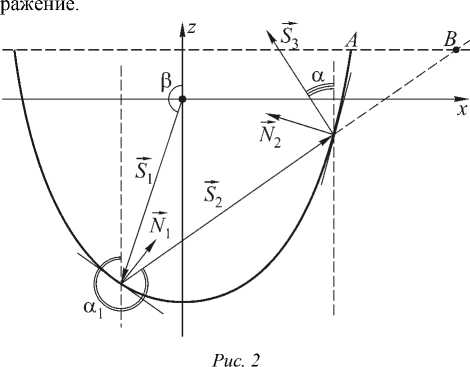
Координата пересечения рассчитывалась следующим образом.

x-x1   z sx

-

sz

z ₁

,

– уравнение прямой, по которой движется луч.

z = r ( ϕ ₀)cos( ϕ ₀),                              (8)

– уравнение прямой, проходящей через крайние точки зеркала.

s x = x ⋅(r(ϕ0)cos(ϕ0)-z1)+x1, sz

где ϕ ₀ – угол крайней верхней точки зеркала, а ( x ₁, z ₁) – точка первого отражения. Если переотра-жений не возникает, то производим расчет интеграла (4) с использованием выражения (6) для α ( β ) .

Если же отраженный луч S ₂ пересекает поверхность зеркала, то необходимо найти координаты точки пересечения отраженного луча и зеркала, т.е. точку второго отражения. Для этого определим разность функций зеркала и прямой, по которой движется луч [4]:

F(ϕ)= szx1 - sxz1 - r(ϕ) , (10) szCosϕ - sx Sinϕ где, (x1,z1) – точка первого отражения. Для нахождения точки найдем такой угол ϕ , при котором F(ϕ) = 0 . Затем воспользуемся законом отражения:

S 3 = S 2 - N 2 ( N 2 ⋅ S 2 ). (11)

В результате получим S₃ – вектор направления луча после второго отражения. Будем повторять приведенные шаги до тех пор, пока луч S_i не попадет в апертуру зеркала. После этого воспользуемся формулой (6) для расчета α ( β ) .

Итак, рассмотрим полный алгоритм трассировки лучей.

Введем сетку по углу β с шагом ∆β . Количество лучей, испускаемых источником, будет равно количеству точек на сетке.

Для каждого луча вышедшего под углом β _k будем определять угол, под которым этот луч выйдет из апертуры зеркала, т.е. зависимость α ( β _k ) . Если происходит только одно отражение, то используем формулу (5). Если происходят многократные отражения, то будем использовать способ расчета, описанный в данном пункте. Причем, если изначально энергия луча была i ₀ , то при каждом отражении будем уменьшать ее согласно формуле:

i n + 1 = i n ⋅ q ,                                            (12)

где q – коэффициент отражения для зеркала.

После расчета всех α ( β _k ) и i ( β _k ) будем считать интеграл (4) численно.

Добавив прямой свет, получим искомую диаграмму направленности.

• 4.    Расчет зеркала заданной диаграмме направленности

Для расчета зеркала r ( β ) был применен итерационный метод, состоящий в градиентной минимизации функционала невязки ε ( r ) , представляющего различие расчетного и требуемого распределений интенсивности. Минимизация функционала невязки (обратная задача) предполагает многократное решение прямой задачи, т.е. расчета ДН от заданного зеркала. Решение этой задачи описано в пунктах 2 и 3 данной статьи.

Функция зеркала задавалась в виде полинома в полярных координатах:

r ( β ) = ∑ c i cos ^{i - 1} ( β ) ,                           (13)

i

В качестве функционала невязки использовалась квадратичная функция

ε ( c ) = ∫ ( I ( α , c ) - I ^~( α ) ) ² d α ,                    (14)

где c – вектор коэффициентов полинома, а I ^~( α ) – эталонная диаграмма направленности. Минимизация функционала (14) происходила относительно коэффициентов полинома (13).

В этом случае градиентный метод расчета функции r ( β ) состоит в итерационной коррекции вектора коэффициентов x по правилу:

c _n = c _{n - 1} - h ∇ε ( c _{n - 1}),                          (15)

где ∇ε ( c ) – градиент функции невязки, а h – шаг метода. Определение вектора градиента осуществляется численно с использованием разностных формул для расчета производных. В работе для минимизации функционала невязки (14) и реализации градиентного метода (15) были использованы java-класс Uncmin_f77 и java-интерфейс

Uncmin_methods из пакета оптимизации AN UNCONSTRAINED NONLINEAR OPTIMIZATION SOLVER.

Для характеристики качества решений, получаемых в результате работы итерационного алгоритма, введем значение среднеквадратической ошибки:

с ₁ = 57,96268; с ₂ = 9,401274; с 3 =- 5,276586 с ₄ =- 12,200411; с ₅ = 0,867428; с 6 = 14,009340 с 7 = 8,330860.

Среднеквадратическая ошибка Ь~ 2,62% .

5 =1 п

I

( I ( a , c ) - ~( a )) ² (~( a )) ²

1/2

da

Теперь рассмотрим способ выбора начального приближения.

Выбор начального приближения является важной частью процесса решения обратной задачи, поскольку целевая функция может иметь несколько локальных минимумов.

По заданной ДН I( a ) определялась функция а ( в ) из решения дифференциального уравнения (1). Данная зависимость однозначно определяет зеркало r ( в ):

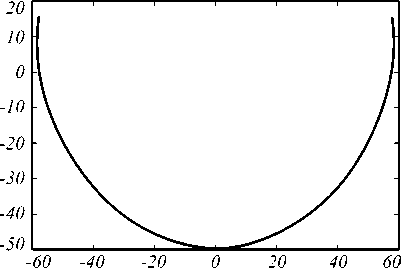
Рис. 4. Сечение полученного зеркала

i   — а(Р) + в + п r (р i) = roexp tgg(               ) d р.

Численно рассчитав интеграл (17), получим набор r ( Р i ). По методу наименьших квадратов подберем коэффициенты полинома (13). Полученные коэффициенты используются в качестве начального приближения.

5. Результаты расчета

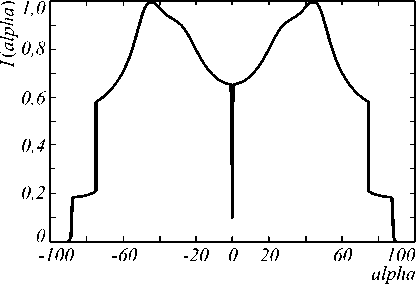
Рис. 5. Полученная диаграмма направленности

Представленный алгоритм был использован для расчета зеркала для формирования ДН, изображен-

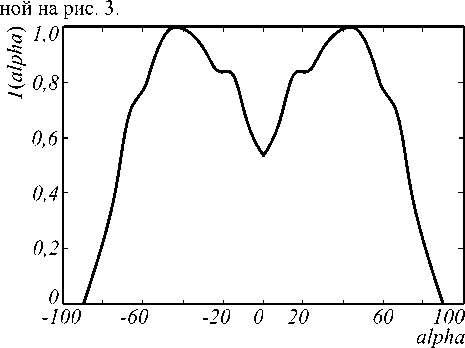
Рис. 3. Эталонная диаграмма направленности

Зеркало было задано в виде полинома (13) шестой степени. В результате расчетов было получено зеркало, представленное на рис. 4. Результирующая ДН приведена на рис. 5. На ней, как и на эталонной диаграмме, наблюдается максимальное значение интенсивности примерно на 45º, а значение интенсивности, составляющее половину от максимального, на 70º.

Расчетные коэффициенты полинома имеют вид:

Заключение

Описанный градиентный метод расчета зеркала по заданной радиально-симметричной диаграмме направленности является эффективным, так как при зеркале, заданном в виде полинома шестой степени, дает ошибку порядка 3%.

Данный метод может быть применен для расчета радиально-симметричных световых приборов прожекторного типа.

Работа выполнена при поддержке грантов РФФИ №07-07-97601-р_офи, 07-01-96602-р_поволжье_а, 07-07-91580-АСП_а, а также при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-SA-06).