Расчет параметров движения приводов механизма параллельной структуры

В настоящее время в таких перспективных отраслях промышленности, как ракетно-космическая техника и станкостроение, актуальной является задача увеличения точности приводов ориентирующих устройств. Обычно для решения этой задачи используются многозвенные рычажные или гибкие манипуляторы [1; 2].

Серьезным недостатком таких манипуляторов является их небольшая жесткость, снижающая точность отработки заданных перемещений и затрудняющая управление приводами. Для устранения указанных недостатков разработаны механизмы с параллельной структурой (дельта-механизмы). Однако применение таких механизмов невозможно без решения прямой и обратной задачи кинематики манипуляторов, которое усложняется наличием нескольких кинематических цепей, налагающих ограничения на перемещения выходного звена [3].

Для решения прямой и обратной задачи кинематики манипуляторов применяются два подхода: компьютерное моделирование (рис. 1) и аналитический расчет [4].

Рис. 1. Компьютерная модель дельта-механизма

Рассмотрим дельта-механизм, содержащий три кинематические цепи, каждая из которых состоит из цилиндрического и сферического шарниров (рис. 2).

Для кинематического анализа дельта-механизмов применяется формула Сомова-Малышева [6]. Общее число H степеней подвижности механизма относительно неподвижного звена (основания) для про- странственной кинематической структуры определяется по формуле

Н = 6·(k – 1) – 5p1 – 4p2 – 3p3 – 2p4 – p5, где k – общее число звеньев кинематической цепи; pi – число пар с i степенями свободы.

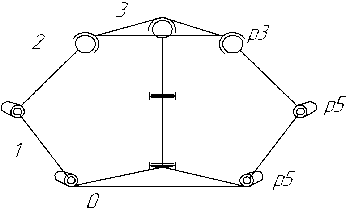
Рис. 2. Схема дельта-механизма [5]:

0 , 1 , 2 , 3 – звенья кинематической цепи; p 3 – сферический шарнир; p 5 – цилиндрический шарнир

Число степеней свободы для модели дельтамеханизма, изображенной на рис. 4, равно трем: две вращательные и одна поступательная.

После определения степеней подвижности дельтамеханизма, при помощи компьютерного моделирования была решена задача нахождения крайних положений выходного звена.

При применении устройств параллельной кинематики для ориентации антенн и телескопов космической техники главным параметром является угол наклона выходного звена Ω с координатами X 1 , Y 1 , Z 1 относительно координат основания X ₀, Y ₀, Z ₀. Графики углового перемещения, полученные при компьютерном моделировании движения дельта-механизма, приведены ниже (рис. 3 - 5).

Задача определения положения выходного звена манипулятора может быть решена не только при помощи компьютерного моделирования, но и аналитически (рис. 6).

Прямая задача кинематики манипуляторов сначала решается для одной кинематической цепи ( l ₁, l ₂, l ₃), при этом другие кинематические цепи, состоящие из звеньев l ′ ₁, l ′ ₂, приняты статичными. Затем аналогичный расчет проводится и для остальных кинематических цепей.

Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева

Рис. 3. Крайнее верхнее положение выходного звена дельта-механизма

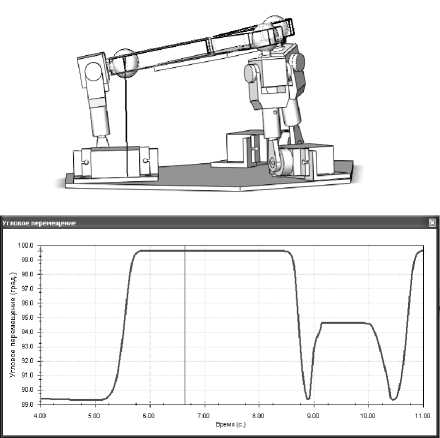
Рис. 4. Промежуточное положение выходного звена

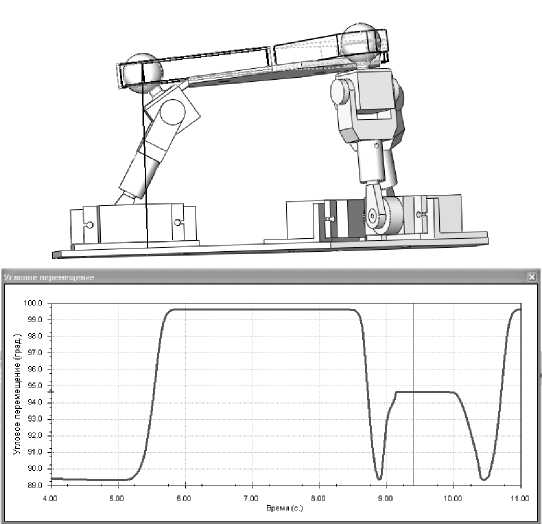
Рис. 5. Крайнее нижнее положение выходного звена

В результате будут получены функции зависимо-

сти координаты выходного координат кинематической щейся в плоскости ZOY :

звена Ω от обобщенных цепи φ 1 , φ 2 , φ 3 , находя-

y : В - 1 1 • cos(ф₁) - 1 2 • cos(ф₂

-

— п + ф 1 ) - 1 3 • sin(Q) = 0,

z : 1 1 • sin(ф₁) + 1 ₂ • sin(ф₂ - — n + Ф 1 ) - 1 3 • cos(Q) = H,

3n- — п-ф1 -ф— -фз = ^-

Для нахождения координат в крайних положениях механизма целесообразно перестроить механизм так, как показано на рис. 7.

Минимальное значение угла Ω (рис. 7, а ) рассчитывается с помощью системы

У : В ^{- 1} ₁ • СО8( ф ! ) ^- ( ¹ — + ¹ з ) • sin( Q m_ln ) = 0,

_< z : 1 1 • sin( ф 1 ) ^- ( 1 2 + 1 3 ) • cos( Q min ) = H ,

^2п- — Л-Ф 1 -Ф 2 =O_m n .

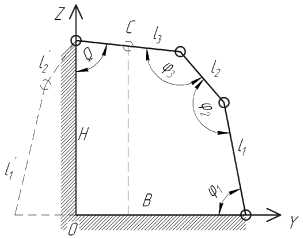
Рис. 6. Расчетная схема дельта-механизма:

l 1 , l 2 ,l 3 — подвижные звенья кинематической цепи; l ' 1 , l'2 - зафиксированные звенья; φ 1 , φ 2 , φ 3 – углы поворота звеньев;

Ω – угол поворота выходного звена; С – центр выходного звена

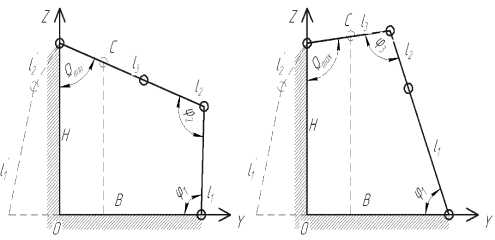
а

б

Рис. 7. Расчетная схема дельта-механизма в крайних положениях:

а – Ω min ; б – Ω

max

Максимальное значение угла Ω (рис. 7, б ) определяется решением системы

y : B ^- ( l i + 1 2 ) • co^s( _{V 1} ) ^- 1 3 • sm( Q max ) = 0, _<  z : ( 1 1 + 1 2 ) • SiB( 9 i ) - 1 3 • COS( Q max ) = H ,

2n--2 Л-Ф1 -Фз =Qmax.

Таким образом, нами выполнен расчет положения выходного звена в механизме параллельной кинематики. Создана компьютерная модель для анализа движения дельта-механизма. Получены данные о крайних положениях устройства параллельной структуры. Найдена система уравнений, описывающая зависимость координат выходного звена от обобщенных координат кинематической цепи.