Расчет параметров модели педагогических измерений

Специфической чертой современного этапа развития теории и практики педагогических измерений следует считать широкое внедрение методов математического моделирования. Математические модели способствуют выполнению двух основных функций теории - объяснению и прогнозированию наблюдаемых результатов тестирования.

^∗ Demenchenok O.G. Calculation of parameters of model of pedagogical measurements.

ВЕСТНИК ВОСТОЧНО-СИБИРСКОГО ИНСТИТУТА МВД РОССИИ

Для практического применения моделей в педагогических измерениях необходимо, прежде всего, определить параметры модели. Затем неизбежно возникает вопрос об адекватности полученной модели – насколько хорошо модель справляется со своими функциями? Подбору параметров и оценке качества модели посвящена данная статья.

Теоретические основы оценки параметров модели измерения

Задача построения математической модели, связывающей уровни подготовленности испытуемых и трудности тестовых заданий с конкретными результатами выполнения теста, может быть сформулирована следующим образом. Из теоретических соображений выбран принципиальный вид зависимости вероятности правильного ответа. Эта зависимость – та или иная модель Item Response Theory (IRT).

Модель содержит ряд параметров: θ – подготовленность испытуемых, β – трудность заданий, а – значение параметра крутизны графика функции задания или различающая способность задания для двух- и трехпараметрических моделей, с – мера возможного угадывания правильного ответа на задание, для трехпараметрической модели. Требуется так выбрать эти параметры, чтобы результаты конкретного тестирования и математическая модель наилучшим образом совпадали.

Решение этой задачи во многом зависит от того, что именно мы условимся считать «наилучшим», т.е. от принятого критерия оптимальности. Можно, например, считать критерием оптимальности минимум максимального отклонения между расчетными и экспериментальными данными; можно потребовать, чтобы в минимум обращалась сумма абсолютных величин отклонений и т.д. При каждом из этих требований мы получим свое решение задачи, свои значения параметров θ и β.

Теоретическую базу всех методов и приемов, положенных в основу построения эмпирических математических моделей, составляет метод максимального (наибольшего) правдоподобия. В общем виде метод максимума правдоподобия можно сформулировать так: наилучшее описание явления то, которое дает наибольшую вероятность получить в результате измерений именно те значения, которые и были фактически получены [1].

В идеальном случае математическая модель полностью соответствует экспериментальным данным. Однако в действительности результаты измерения всегда содержат погрешности. В связи с этим имеет место множество гипотез, не противоречащих опытным данным. Метод максимального правдоподобия состоит в выборе такой гипотезы, при которой вероятность получить в процессе измерения фактически наблюдаемые величины была бы максимальной. В формальной записи этот метод может быть представлен в виде максимума произве- дения вероятностей всех наблюдаемых независимых событий [2]:

N

Pi • P 2 • - ’ P n = П Pi ^ max (1)

i = 1

Ещё один известный метод – метод наименьших квадратов - это метод теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. По этому методу требование наилучшего согласова- ния расчетных х и эксперименталь ных х0 данных сводится к тому, чтобы сумма квадратов отклонений между ними обращалась в мини- мум:

N

Е ⁽ х ^{- х} о i ) 2 ^ min        (2)

i = 1

Метод наименьших квадратов приводит к сравнительно простому математическому способу оценки параметров; кроме того, он допускает довольно веское теоретическое обоснование с вероятностной точки зрения.

Критерии подбора параметров модели Раша по методу максимума правдоподобия

Вернемся к задаче подбора параметров модели. Предположим, из теоретических соображений выбрана модель Г. Раша. По этой мо- дели вероятность результата х при решении i-ым тестируемым j-го за- дания определяется выражением:

P ij ( x ) =

_e x ij ( θ i - β j )

подготовленности i -го тестируемого; в j - уровень трудности j -го задания.

По методу максимального правдоподобия наилучшим будет признан тот набор значений O и в , при котором произведение расчетных вероятностей фактически полученных результатов максимально: n m                n m x ij ( θ i - β j )

ПП j ' ) = ПП     ^ max (4)

i=1 j=1                i=1 j=1 1 +e i j где n - количество испытуемых; m -число тестовых заданий.

Особенность модели Г. Раша заключается в том, что она оперирует только разностью параметров O и β . Поэтому можно получить бесконечное количество «наилучших» решений, отличающихся на произвольную постоянную величину:

O- в = (O + С) - (в + С) = O- в.

Для определенности целесообразно ввести ограничение, например, в виде равенства нулю среднего значения уровня подготовленности всех испытуемых:

O = 0.                      (5)

В этом случае наилучшее решение будет единственным. Для реализации в вычислительных алгоритмах желательно преобразовать ограничение (5) в неравенство:

I I ^{5 5} ,                      (⁶)

где £ - некоторая допустимо малая величина, например равная 0,001.

Выражений (4) и (6) достаточно для непосредственного численного решения задачи подбора параметров модели.

По методу наибольшего правдоподобия можно получить ещё один вариант решения, основанный на том, что в точке экстремума (максимума или минимума) производная функции равна нулю.

Зная, что ea eb = ea+b, преобра зуем числитель условия (4):

nm

ZZ js,- Pj) e* ^

--> max nm ПП( + e'"j i=1 j=1

Введём обозначения: R i –

сумма результатов выполнения тестовых заданий i -м тестируемым ( R i также называют исходным баллом):

m

R  Z Xj(8)

j = 1

s j – сумма результатов выполнения

Используя (8) и (9), заменим nmn

ZZ x. = Z RA(10)

i=1 j=1

nmm

ZZ 1i = Zs,p,(11)

1=1 j=1

Таким образом, уравнение (7)

принимает вид

nm

ZR'i-Z■ в e"

nm

ПП 1 + e ^{e j} )

i = 1   j = 1

^ max (12)

Так как логарифм – монотонно возрастающая функция, то максимум функции правдоподобия совпадает с максимумом ее логарифма:

j -го задания всеми тестируемыми

n sj=Z xn

i = 1

ln

nm

Z R '-Z S j P j

e

j = 1

A

П П ⁽ 1 + e ^{A -} j

V - = 1 j = 1                J

^ max

Для нахождения максимума функции правдоподобия найдем и при- равняем нулю частные производные логарифмической функции правдопо- добия по каждому из аргументов:

n      m      nm d Z R.-Z zA-ZZ ln(1+e6"j

V i=1___________j=1____________i=1 j=1____________________J m    p6- — P,

e

R i  Z 1 + e '- ^p j

= 0

или

m     .6-- _{P 1}

R -У--= 0

, i  ^-^H + eA в n     m      nm a ZRA-ZSjP.-ZZIn(1 + e'

V i = 1             j = 1              i = 1 j = 1

дв,

^{6 -} . )' J

-

s j

n

+Z

i = 1

_e ^{6 -} e i + e^

= о ,

e6-e или  s,-Z.,  . -e =0.

i = 1 1 + e ¹

Нетрудно заметить, что выражение (14) представляет собой разность между суммой результатов выполнения заданий i -м испытуемым и суммой вероятностей правильных ответов на все задания для того же испытуемого. Аналогично, уравнение (15) представляет собой разность между суммой результатов выполнения задания всеми тестируемыми и суммой вероятностей правильных ответов на то же задание для всех испытуемых.

В итоге мы получаем второй вариант решения по методу наибольшего правдоподобия. Он состоит из n уравнений (14) (по одному уравнению на каждого тестируемого для i =1, 2 … n ) и m уравнений (15) (по одному на каждое задание), которые нужно численно решить с учетом дополнительного ограничения, например (6), для нахождения параметров модели Г. Раша. Наличие аналитических зависимостей для частных производных упрощает и существенно ускоряет поиск решения. Поэтому многие алгоритмы подбора параметров модели Г. Раша основаны на уравнениях (14) и (15).

Критерий подбора параметров модели по методу наименьших квадратов

Сформулируем условие оптимальности подбора параметров модели, используя метод наименьших квадратов. По этому методу приближённые значения параметров находятся из условия минимизации суммы квадратов отклонений между моделью и наблюдаемыми результатами.

Отклонение (различие) между моделью и наблюдаемыми результатами может быть найдено как разность результата выполнения задания xij и вероятности правильного ответа Pij: для правильного ответа xj - Pij = 1 - Ру, для неправильного ответа xj - Pij = 0 - Pij = - Pij.

Разность х_у - P y показывает, насколько расчетная вероятность правильного ответа отличается от идеального значения: для правильного ответа P ij должна стремиться к единице, а для неправильного ответа – к нулю.

Тогда критерий минимума квадратов отклонений для обеих рассматриваемых моделей формулируется в виде условия: nm             ²

ZS x j -.. - .,W - в )  ^ min 16)

i = 1 j = 1 V       1 + e          7

В ходе пробных расчетов выявлено, что в ходе поиска решения иногда отмечается существенный рост значений 0 . Поэтому условие (6) дополнено вторым ограничением, устанавливающим пределы изменения 0 от - 5 до + 5:

1 ⁰ max ^ ⁵              (17)

Подбор параметров модели в электронной таблице Microsoft Excel.

Все расчеты могут быть выполнены в Microsoft Excel, доступном и широко известном средстве автоматизации вычислений. Excel способен находить экстремум

ПРОБЛЕМЫ ДЕЯТЕЛЬНОСТИ ОВД И ГПС функции одной или нескольких переменных. Кратко опишем технологию поиска параметров модели Г. Раша по методу максимального правдоподобия для представленных в табл.1 результатов тестирования (принцип решения остальных задач аналогичен). Сначала вводим данные табл.1 в клетки В2:О35 (рис.1).

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
1		4	5	7	6	9	8	10	11	13	12	14	15	16	17
2	25	0	1	0	1	0	0	0	0	0	0	0	0	0	0
3	4	1	0	1	0	1	0	0	0	0	0	0	0	0	0
4	33	1	0	1	0	0	0	1	0	0	0	0	0	0	0
5	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0

Рис.1. Ввод исходных данных

Находим сумму баллов каждого тестируемого: в клетку Р2 вводим =СУММ(B2:O2) и копируем эту формулу в клетки Р3:Р35. Для суммы баллов по каждому заданию в В36 вводим =СУММ(B2:B35) и копируем в С36:О36.

Рассчитываем начальные значения параметров модели: - для уровней подготовленности испытуемых в Q2 вводим =LN(P2/(14-P2)) и копируем в клетки Q3:Q35 (14 – число тестовых заданий);

• -    для уровней трудности заданий в В37 вводим =LN((34-B36)/B36) и копируем в С37:О37 (34 – количество испытуемых).

Определяем вероятности результатов выполнения тестовых заданий, для чего в В42 вводим =ЕСЛИ(B2>0;1/(1+EXP((-1)*($R2-B$38)));1-1/(1+EXP((-1)*($R2-B$38)))) и копируем в клетки В42:О75. Если значение в клетке B2 больше нуля (задание выполнено правильно), то рассчитывается вероятность правиль- ного    ответа    по    формуле

1/(1+EXP((-1)*($R2-B$38))); в противном случае – вероятность неправильного ответа

1-1/(1+EXP((-1)*($R2-B$38))). Для расчета параметров двухпараметрической модели вместо сомножителя (1) следует записать адрес клетки со значением дифференцирующей способности задания.

Зададим параметры модели, равные начальным:

• -    выделим начальные значения уровней подготовленности испытуемых Q2:Q35 и вставим значения в R2:R35, для чего нажмем кнопку Копировать , щелкнем в клетке R2 и выберем в меню Правка – Специальная вставка – Значения ;

• -    для уровней трудности выделяем В37:О37 и вставляем значения в В38:О38.

В клетку R36 введем формулу модуля среднего значения уровней подготовленности =ABS(СРЗНАЧ(R2:R35)) .

Найдем произведение всех вероятностей: в R38 введем =ПРОИЗВЕД(B42:O75) . В клетке R38 появляется 1,66431E-58, т.е. начальное значение вероятности всех ответов очень мало – 1,66 ⋅ 10^-58. Так как механизм поиска решения Excel требует, чтобы значения критерия и, следовательно, его изменения при подборе параметров не были бы слишком малы, то удобнее искать максимум логарифмической функции правдоподобия. Для этого в клетку R39 введем =Ln(R38) .

Проверим, установлен ли механизм поиска решения: выберем в меню Сервис – Надстройки, поставим отметку в пункте Поиск решения и нажмем ОК. Далее нужно выполнить команду Сервис – Поиск мулой критерия оптимальности;

• 2)    указать направление поиска, отметив пункт Равной максимальному значению ;

• 3)    в поле Изменяя ячейки ввести адреса ячеек, значения которых будут варьироваться в процессе поиска решения. В нашем случае это R2:R35; В38:О38 (удобно

вводить, выделяя клетки с помощью мыши, второй диапазон при нажатой клавише Ctrl );

• 4)    с помощью кнопки Добавить ввести ограничение: значение В36 ≤ 0,001;

• 5)    нажав кнопку Параметры , указать параметры поиска в соответствии с рис.3. Это повысит точность подбора параметров.

После щелчка на кнопке ОК решения и заполнить диалоговое получим решение поставленной за- окно (рис.2):

дачи. В клетке R38 находится мак-

• 1)    кликнуть левой клавишей мыши в поле Установить целевую ячейку (т.е. клетку, значение которой необходимо максимизировать или минимизировать), пе-

• симальное значение вероятности всех данных, равное 5,09⋅10-48. Значения уровней подготовленности, найденные по методу наибольшего правдоподобия, записаны в клетках

реместить указатель мыши и R2:R35, уровней трудности заданий кликнуть на ячейке R39 с фор- – в ячейках В38:О38.

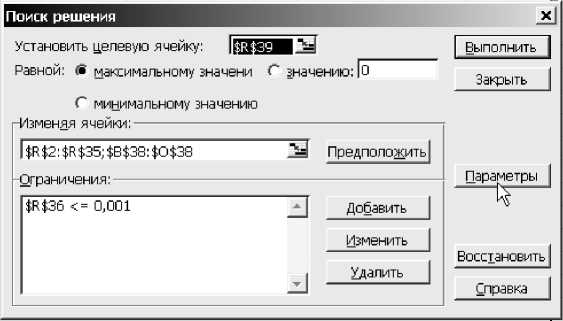
Рис.2. Окно поиска решения

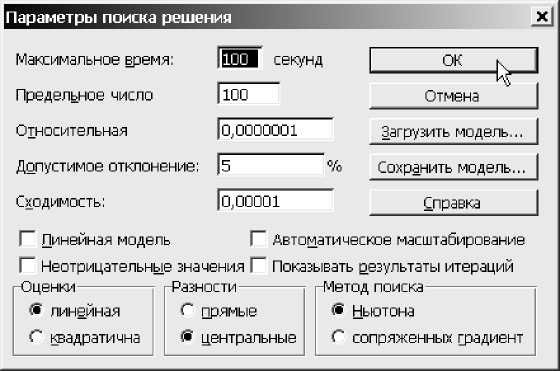
Рис.3. Рекомендуемые параметры поиска решения

Анализ результатов подбора параметров модели

Насколько отличаются параметры модели измерения, найденные по разным методикам? Для ответа на этот вопрос сравним результаты решения одной и той же задачи, полученные разными способами. Для примера взята задача подбора параметров модели Г. Раша из известной работы Б.Д.Райта и М.Х. Стоуна [3].

Анализ результатов подбора параметров модели свидетельствует:

• 1)    значения параметров существенно зависят от выбранной модели и метода расчета;

• 2)    характер изменения параметров θ и β для всех рассмотренных моделей и методов подобен. Это подтверждает корреляционный анализ – коэффициент корреляции для уровней подготовленности составляет от 0,92 до 0,99, для уровней трудности от 0,94 до 0,99, что свидетельствует об очень сильной статистической взаимосвязи;

• 3)    значения дифференцирующей способности заданий, найден-

• ные по методу максимального правдоподобия и программой Winsteps хорошо согласованы (коэффициент корреляции 0,90). Однако эти значения слабо согласованы с результатами по методу наименьших квадратов (коэффициент корреляции 0,17);

• 4)    равным начальным уровням подготовленности испытуемых (т.е. одинаковым суммам результатов тестирования R i ) соответствуют равные итоговые значения по всем методикам расчета для модели Г. Раша, за исключением метода наименьших квадратов;

• 5)    аналогично, равным начальным уровням трудности тестовых заданий (т.е. одинаковым суммам выполнения задания всеми тестируемыми s j ) соответствуют равные итоговые значения по всем методикам расчета для модели Г. Раша, за исключением метода наименьших квадратов;

• 6)    для двухпараметрической модели равным начальным уровням θ и β могут соответствовать разные итоговые значения, как по методу максимального правдоподобия, так

ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ РЕАКЦИЙ НА СИГНАЛЫ ОПАСНОСТИ У ЛЮДЕЙ ПОЖИЛОГО ВОЗРАСТА

В.А. Помыткин, начальник отдела обеспечения пожарной безопасности объектов высших органов государственной власти Центра обеспечения деятельности ФПС МЧС России

В работе изучается влияние различных средств и способов оповещения на действия пожилых людей наиболее часто встречающиеся действия при угрозе их жизни для выработки рекомендаций для участников тушения и спасения пострадавших.

The purpose of this work is studying influence of various means and ways of the notification on actions of older persons, studying of most often meeting actions at threat of their life and a life of associates and development of recommendations for firemen and rescuers ^∗ .

^∗ Ermakov A.R., Pomitkin V.A. Research the danger signals features reactions of elderlys people.