Расчет параметров передачи модового состава промышленных образцов кварцевых оптических волокон c увеличенным диаметром сердцевины

В настоящее время для ряда практических приложений возникает задача расчета параметров передачи модового состава уже изготовленных промышленным способом и соответствующим образом протестированных образцов оптических волокон (ОВ). В этом смысле не являются исключением и волоконные световоды с увеличенным относительно традиционных одномодовых ОВ диаметром сердцевины, ориентированные на многомодовый или маломодовый режим передачи оптического сигнала. В качестве примера можно привести традиционное сопоставление полученного в ходе моделирования теоретического прототипа с результатами его опытной реализации и проведением последующей оценки влияния отклонения параметров последнего от оптимизированных значений на дисперсионные характеристики мод искомых порядков.

В данной работе представлена методика расчета параметров передачи модового состава промышленных образцов кварцевых ОВ с увеличенным диаметром сердцевины, отличающихся от традиционно используемого как в строгих, так и приближенных методах анализа волоконных световодов модельного представления с несимметричной геометрией структуры поперечного сечения, как с точки зрения радиальной координаты, так и формы профиля показателя преломления.

Проблемы расчета параметров передачи модового состава промышленных образцов оптических волокон с увеличенным диаметром сердцевины

Сегодня известно достаточно большое число приближенных методов анализа волоконных световодов и их различных модификаций, часть которых также позволяет проводить расчет параметров передачи не только основной, но и мод высших порядков [1-6]. Вместе с тем применение большинства приближенных методов для решения задачи анализа промышленных образцов ОВ существенно ограничено. В первую очередь данный факт объясняется вынужденной аппроксимацией реального профиля показателя преломления, отличающегося достаточно сложной формой, с помощью набора гладких функций, а в ряде методов – и вовсе одной (так называемый a- профиль показателя преломления), в то время как профиль показателя преломления реальных ОВ даже последних поколений существенно отличается от модельного сглаженного как минимум отклонениями от оптимизированной гра- диентной формы и локальными флуктуациями показателя преломления [7-8]. Кроме того, большинство указанных подходов ориентировано на анализ симметричных ОВ круглого сечения, но, как показывают экспериментальные данные, ни профиль показателя преломления, ни радиальное сечение реальных ОВ не являются симметричными [2; 7-8].

Очевидно, что задача анализа волноведущей диэлектрической структуры, которую представляет собой некруглый несимметричный волоконный световод, может быть решена с помощью строгих численных сеточных методов, в частности таких, как метод конечных элементов (МКЭ) и метод конечных разностей (МКР), а также их разнообразные модификации [1; 4-6; 9-10]. Однако и в этом случае переход к расчету ОВ сложной геометрии при одновременно увеличенном диаметре сердцевины связан с целым рядом проблем.

Во-первых, для подобных волоконных световодов число направляемых мод, находящихся в диапазоне собственных значений постоянной распространения Pi удовлетворяющих условию отсечки, даже в рамках приближения слабонаправляющего оптического волновода в рабочем телекоммуникационном диапазоне длин волн без учета поляризации, может достигать от нескольких десятков до сотни и более. При векторной постановке задачи это значение может увеличиваться на порядок и более. При этом число решений системы линейных алгебраических уравнений (СЛАУ), получаемой в результате применения МКЭ для анализа таких ОВ, во всем диапазоне направляемых мод может быть настолько велико, что реализовать поиск всей совокупности собственных значений постоянных распространения модового состава исследуемого ОВ даже на высокопроизводительных ЭВМ не всегда представляется возможным.

Во-вторых, для подобных ОВ требуется существенное увеличение числа элементов, необходимых для дискретизации заданной области и, как следствие, повышение требований к вычислительной мощности ЭВМ и объему оперативной памяти. Формально данная проблема частично преодолима за счет роста производительности современных многопроцессорных ЭВМ. Однако далее возникает задача корректной реконструкции 3D-структуры исследуемого промышленного образца ОВ. В рассматриваемом случае наиболее полный состав исходных данных к расчету содержат протоколы измерения профиля показателя преломления ОВ, выполненные штатным комплектом соответствующего лабораторного оборудования – анализаторов ОВ.

Данные средства измерений позволяют не только определять диаметр поля моды, эффективную область излучения и геометрию сердцевины и оболочки, но и осуществлять сканирование профиля показателя преломления с достаточно высоким разрешением – менее 0,5 мкм по радиальному сечению ОВ и менее 0,0001 по абсолютной разности показателя преломления исследуемого образца в заданной точке поперечного сечения и калибровочного значения показателя преломления чистого кварца SiO2. (см. [11] и др.).

Измерение профиля показателя преломления реализуется на основе метода ближнего поля (refracted near-field method) [12-13] и проводится на оптической несущей области «коротких длин» волн X = 630 … 690 нм. Полученные данные фактически представляют собой массивы распределения отклонения показателя преломления от номинального значения для чистого кварца SiO₂ на рабочей длине волны источника излучения анализатора (в данном случае X = 670 нм) по условным радиальным сечениям тестируемого волоконного световода «Х» и «Y», число элементов которых определяется разрешающей способностью самой установки.

Таким образом, при анализе промышленных образцов ОВ строгими сеточными методами МКЭ и МКР в первую очередь возникает проблема детализированной реконструкции искомой 3D-структуры исследуемого волоконного световода с учетом ограниченного набора исходных данных, представляющих собой распределение значений отклонения показателя преломления по радиальным координатам осей абсцисс и ординат в плоскостях двух радиальных сечений «Х» и «Y».

Разработка методики реконструкции 3D-структуры несимметричного волоконного световода на основе данных протоколов измерения профиля показателя преломления штатным комплектом анализатора оптических волокон

Для решения описанной задачи предлагается рассмотреть «worst case» («худший случай») на примере анализа промышленного образца многомодового ОВ 50/125 первого поколения кат. ОМ2. Согласно протоколам измерений профиля показателя преломления, данный образец ОВ отличается разбросом значений радиуса сердцевины в условных сечениях «Х» и «Y» до 0.47 мкм

[7-8]. Градиентный профиль ОВ содержит центральный габаритный дефект в виде провала, а также сильные локальные флуктуации показателя преломления. На рис. 1а представлены результаты сопоставления восстановленных на основе протоколов измерений распределений значений относительного отклонения показателя преломления от показателя преломления оболочки по координатам осей условных радиальных сечений «Х» и «Y» сердцевины исследуемого ОВ, на рис. 1б – выделенная центральная область сердцевины.

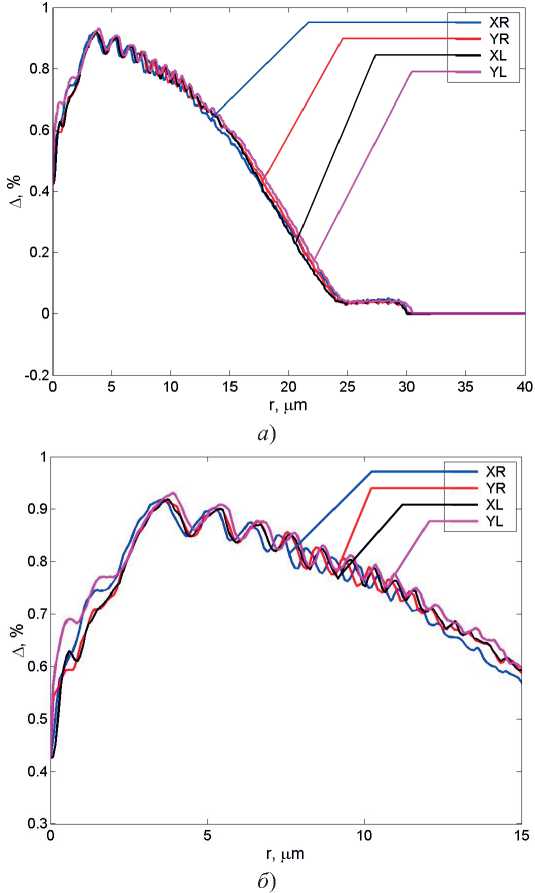
Рис. 1. Сопоставление профилей показателя преломления промышленного образца ОВ 50/125 кат. ОМ2, восстановленных по данным протоколов измерений [7-8], в условных радиальных сечениях «Х» и «Y»: а ) сердцевины и прилегающая к границе раздела оболочка; б ) центральная область сердцевины

Здесь хорошо заметно не только расхождение радиусов сердцевины на всех четырех выделенных полуосях поперечных сечений, но и отклонения по экстремумам локальных флуктуаций показателя преломления в центральной области сердцевины. Число элементов массива показателя преломления в каждом из «полусечений» также неодинаково и варьируется от 402 до 407 точек. Для удобства в декартовой системе координат плоскости радиального сечения ОВ предлагается выделить полуоси «XR», «XL», «YR» и «YL», где индекс «R» соответствует положительным значениям координат, а «L» – отрицательным.

Таким образом, задача восстановления 3D-структуры исследуемого «реального» промышленного образца ОВ заключается в определении промежуточного значения показателя преломления nV для соответствующей ему k -ой пары

™™™ значений и nq из протокола измерения профиля и непосредственно его проекций г\ иГ У , лежащих на полуосях декартовых координат, которые образуют четверть радиального сечения исследуемого ОВ. Здесь ПУ и ПУ являются значениями показателя преломления, соответствующими координатам '^ и У . При этом полагается, что nJq^nJP.-

Предлагаемое решение базируется на предположении, что искомое промежуточное значе-(О ние показателя преломления п \ удовлетворяет уравнению некоторого наклонного эллипса, малая полуось которого соответствует непосредственно проекции ^2 - Уд ) ■ Большая полуось (t)

^п jl является гипотенузой прямоугольного треугольника с катетами, представляющими собой проекцию ^rjp и разность проекций искомого промежуточного значения п \ показателя преломления на ось «3» АпУ = пУ — пУ . В результате данный эллипс находится в плоскости, образующей угол <р к опорной плоскости попе-

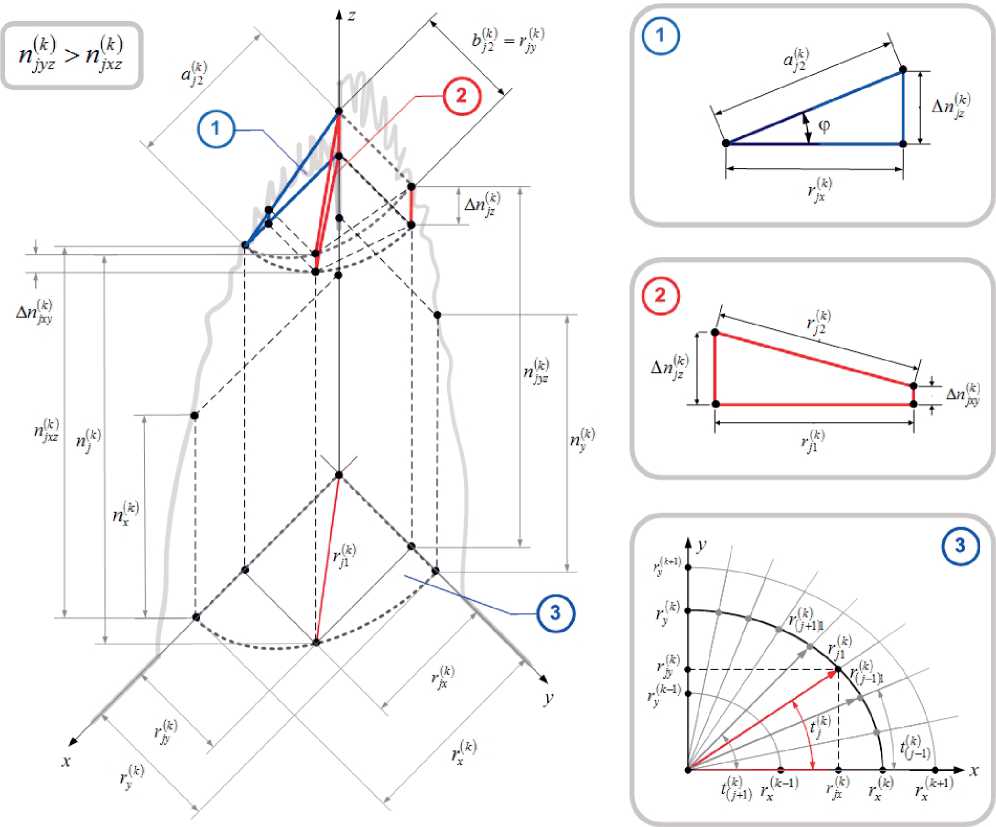
Рис. 2. Определение искомого промежуточного значения показателя преломления п V для соответствующей ему ^-ой пары значений пУ и пУ из протокола измерений профиля показателя преломления исследуемого О В

речного сечения исследуемого ОВ, тангенс угла наклона которого определяется соотношением указанных параметров tg(p = ^/r^.

На рис. 2 приведено графическое представление предлагаемого решения на примере выполнения неравенства соотношения проекций искомого промежуточного значения показателя преломления n\ на оси координат декартовой системы Л > 77 .

Описанная задача решалась с применением неравномерной сетки представления. Здесь на первом этапе были локализованы экстремумы профилей показателя преломления, восстановленных на основе протоколов данных измерений, для каждой из координатных полуосей, формирующих условные четверти поперечного сечения, исследуемого ОВ (см. рис. 1 а-б ). Далее определены соответствующие им значения радиальных координат и номера массивов данных [ x ] и [ y ] протоколов декартовой системы ( x, y ).

После этого для каждого диапазона значений радиальной координаты соответствующей полуоси между соседними экстремумами профиля были переопределены шаг шкалы значений /V^ и на основе него сам фрагмент массива радиальной координаты [ r_p/q ] соответствующей полуоси так, чтобы номера элементов массива локальных экстремумов профиля показателя преломления для всех четырех полуосей координат базовой декартовой системы были идентичны и соответствовали максимальному из четырех ранее выявленных номеров элементов массивов координат этого экстремума.

Для полученных новых массивов радиальных координат [ r_p/q ] каждой из четырех полуосей с применением сплайн интерполяции были переопределены соответствующие значения показателя преломления. На рис. 3 приведен пример задаваемой неравномерной сетки представления несимметричной структуры четверти поперечного сечения ОВ, образованного полуосями « x_R » и « y_R »

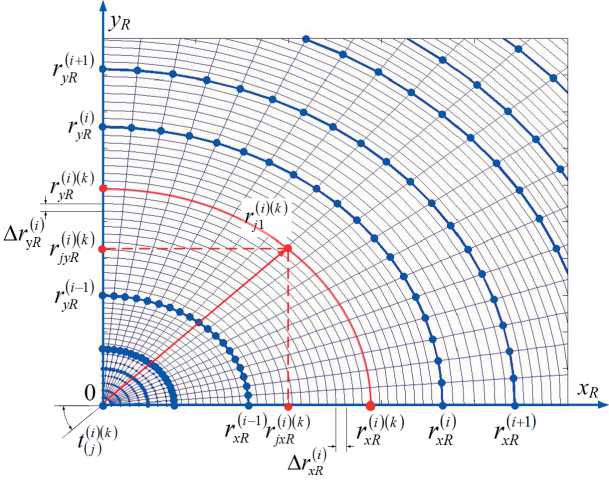
Рис. 3. Неравномерная сетка представления несимметричной структуры четверти поперечного сечения ОВ « x_R y_R »: центральная область сердцевины исследуемого ОВ

Как было отмечено выше, в соответствии с предложенным подходом предполагается, что искомое промежуточное значения показателя преломления ^п^ удовлетворяет уравнению некоторого наклонного эллипса с большой и малой полуосями а> ^ . Проекцией последнего на опорную пло скость радиального сечения исследуемого ОВ также является эллипс с большой и малой полуосями ^и Ь^', а его уравнению непосредственно удовлетворяет проекция п. ’ с координатами на опорной плоско сти рдиаль-ного сечения в полярной системе ^jX ^‘^V^ и ^ЛЛ^ в декартовой.

После подстановки в уравнение эллипса соотношений, связывающих координаты полярной и декартовой систем, получаем выражение для радиальной координаты полярной системы на опорной плоскости сечения ОВ:

^^^чПит^2^^ + [^у^]2 COS2^'*)^  .

В зависимости от соотношения проекций искомого промежуточного значения показателя преломления п\ на ось « z » декартовой системы координат 1Л И /7^ искомое промежуточное значение показателя преломления Л вычисляется следующим образом:

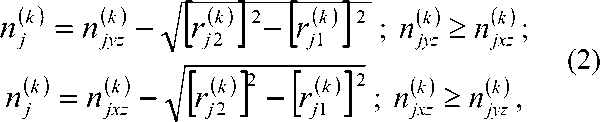
где r^ = V^-? + [yj^]² ; n^ > n^;

„№>„№. _аМ-М. М__ГМ. М_М. ^rijxz - ^гЧу; ’                     - Чу ’ ^uj\ - Чу *

ьЧ = ^; ^ = VRT+HFh

ЧММЧ ьЧ=ьЧ=Ч\

^=7ЙТ+ЙТ;

ЧЧ _ (Ч^. ^.-^зх Ж

ЛЧ_ЧЧ^Ь^ . /)_>ч_хч^_г^ Уп - ^rjy 7М ’ ^72 Чу - -42 Чх

На основе представленной методики была проведена реконструкция 3D-структуры исследуемого промышленного образца ОВ по данным протоколов измерения профиля показателя преломления (см. рис. 1 а-б ), результаты которой в центральной области сердцевины представлены на рис. 4 а .

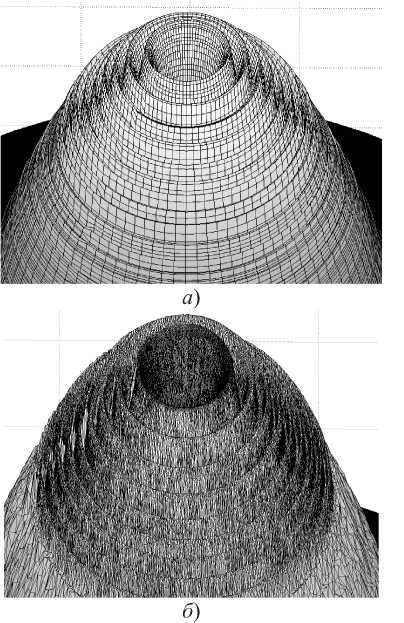
Рис. 4. Фрагмент реконструкции 3D-структуры центральной области сердцевины образца многомодового ОВ: а ) восстановление 3D-структуры на неравномерной сетке по данным протоколов измерения профиля показателя преломления ОВ; б ) наложение адаптивной нерегулярной треугольной сетки после процедры триангуляризации

Это позволяет перейти к известной процедуре формирования переменной адаптивной треу- гольной сетки представления, анализируемого ОВ для последующего расчета нормированной постоянной распространения направляемых мод заданного порядка с помощью строгих сеточных методов. Результаты наложения адаптивной нерегулярной треугольной сетки после проведения процедры триангуляризации, восстановленной по предложенной методике 3D-структуры исследуемого ОВ в центральной области сердцевины, приведены на рис. 4б.

Результаты расчета промышленного образца многомодового оптического волокна

Апробация разработанной методики проведена на примере расчета описанного выше промышленного образца многомодового ОВ 50/125 кат. OM2 (см. рис. 1 а-б ), который отличается сильной несимметричностью (отклонение радиуса сердцевины на полуосях поперечного сечения «X» и «Y» достигает 0,47 мкм), а также наличием центрального габаритного технологического дефекта градиентного профиля в виде провала и сильными локальными флуктуациями показателя преломления.

На первом этапе 3D-структура исследуемого ОВ была восстановлена на основе протоколов измерения профиля показателя преломления [7-8] по предложенной методике на базе неравномерной сетки с узлами на полуосях поперечного сечения, соответствующих экстремумам профиля (см. рис. 4 а ). После чего была проведена процедура триангуляризации с наложением адаптивной нерегулярной треугольной сетки (см. рис. 4 б ) и выполнен расчет параметров передачи модового состава исследуемого ОВ с помощью строгого численного метода смешаных конечных элементов (МСКЭ) [14], адаптированного на случай анализа волоконных световодов с увеличенным диаметром сердцевины [15-17].

Для сравнения также рассматривалось симметричное модельное ОВ, структура которого задавалась в соответствии с протоколами измерения профиля показателя преломления исследуемого промышленного образца ОВ, однако при этом использовались данные измерений на полуоси «xR». Расчет параметров передачи направляемых мод проводился в спектральном диапазоне Л = 800…1350 нм. На рис. 5а приведены спектральные характеристики относительной погрешности нормированной постоянной распространения для основной моды LP01 и некоторых направляемых мод высших порядков LP31, LP22 и LP31. Данный параметр определяется относитель- но постоянной распространения р известным выражением [1-6] вида:

p-konN

^О^йтах -k₀H_N

где k_Q = 2л/Л – волновое число; n _max – максимальное значение показателя преломления сердцевины; n_N – показатель преломления оболочки. Сопоставление полученных результатов показывает, что максимальное отклонение по нормированной постоянной распространения направляемых мод во всем исследуемом диапазоне длин волн составляет менее 0,65%.

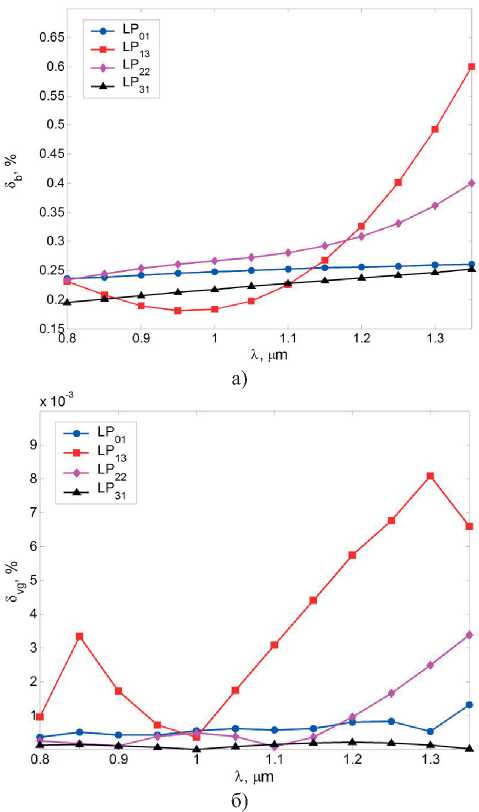
Рис. 5. Относительная погрешность нормированной постоянной распространения а ) и групповой скорости б ) основной и некоторых высших мод «реального» и модельного ОВ

На рис. 5б приведены диаграммы относительной погрешности групповой скорости v_g основной моды LP ₀₁ и перечисленных выше направляемых мод высших порядков, а на рис. 6

– абсолютная разность значений коэффициента хроматической дисперсии D этих направляемых мод в указанном диапазоне длин волн. Здесь по групповой скорости погрешность не превышает £_Vg = 0.10%, в то время как отклонение по коэффициенту хроматической дисперсии составляет менее 2,00 пс/(нм-км).

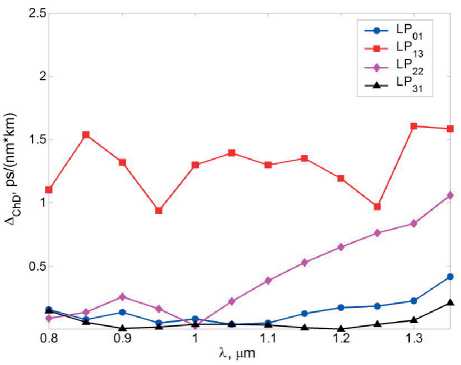
Рис. 6. Абсолютная разность коэффициентов хроматической дисперсии основной и некоторых высших мод «реального» и модельного ОВ

Заключение

Сопоставление полученных результатов позволяет сделать заключение о потенциальной возможности замены несимметричной структуры, характерной для реальных промышленных образцов ОВ, на модельную симметричную, но также восстановленную по соответствующим данным протоколов измерений профиля показателя преломления исследуемого ОВ, при расчете параметров передачи модового состава для последующего проведения моделирования процессов распространения оптических сигналов и/или расчетов показателей качества каналов сравнительно низкоскоростных мультигигабитных систем до 40 Гбит/с [9].

В этом случае формально можно пренебречь проявлением поляризационной модовой дисперсии и достаточно малым отклонением параметров передачи мод «реального» и «модельного» ОВ. Однако при переходе на более высокие скорости очевидно, что даже столь малые расхождения дисперсионных параметров, обусловленные несимметричной структурой промышленных образцов реальных ОВ относительно модельных, могут являться критическими в условиях маломодового режима передачи оптических сигналов в маломодовом режиме передачи оптических сигналов. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-60015 мол_а_дк.