Расчет параметров (постоянная распространения, фазовая и групповая скорости) волоконного световода с градиентным профилем

Постоянная распространения – это параметр, определяющий быстроту распространения электромагнитной волны в волноводе. Постоянная распространения зависит от свойств волновода, таких как его геометрия, показатель преломления и частота волны. Она определяет, как электромагнитная волна изменяет свою амплитуду и фазу при прохождении через волновод. Постоянная распространения является важным параметром при анализе и проектировании волноводных систем. Она позволяет определить, какие моды могут существовать в волноводе и как они будут взаимодействовать друг с другом. Существует несколько способов определения постоянной распространения, включая численные методы (такие как метод конечных элементов или метод конечных разностей), аналитические выражения (публикации [1–6], из относительно недавних работ [7– 10], общие сведения в [11 – 14]), экспериментальные измерения (такие как измерение мощности в разных точках волновода или измерение фазового сдвига при прохождении волны через волновод). Для определения фазовой скорости можно использовать различные методы, такие как интерферометрия или методы временной задержки. В целом, в зависимости от конкретной задачи и типа волновода выбирается наибо- лее подходящий метод определения постоянной распространения.

Также можно выделить несколько последних публикаций по данной тематике с более строгим с математической и физической точек зрения анализом. Так, в работе [15] авторы исследовали проблему межмодовой дисперсии внутри группы оптических вихрей с азимутальным числом |/| > 1 в круглых оптических волокнах. Численно получена и проанализирована зависимость дисперсии оптических вихрей от длины волны для волокон с градиентом и ступенчатым индексом с переменными параметрами. Установлена возможность дисперсии нулевой моды в волокнах со ступенчатым индексом. В статье [16] изучена дисперсия оптических вихрей в скрученных эллиптических волокнах с крутильными механическими напряжениями. На основе спектров вихревых мод скрученных эллиптических волокон со ступенчатым и градиентным профилями установлены аналитические выражения для поляризационного, топологического и гибридного типов дисперсии оптических вихрей. Показано, что для оптических вихрей с высшими значениями топологического заряда все виды дисперсии могут иметь почти нулевые значения как при ступенчатом, так и при градиентном профилях. В публикации [17] рассмотрена структура мод более высокого порядка в мультиспиральных оптических волокнах при наличии механического напряжения кручения. Показано, что при некоторых значениях шага такие моды представляют невырожденные оптические вихри с круговой поляризацией, устойчивые к внешним возмущениям формы поперечного сечения. На основе аналитических выражений для постоянных распространения таких вихревых мод исследуются поляризационная, топологическая и гибридная дисперсии вихревых мод.

В публикации [18] предложена уточнённая модель распределения показателя преломления для волноводов, изготовленных с помощью ионного обмена. В статье [19] предложен простой метод измерения показателя преломления для волокна со ступенчатым показателем преломления, основанный на сканировании оптической мощности радиального смещения.

Цель нашей работы – для слабонаправляющего круглого в поперечном сечении волновода с произвольным градиентным профилем показателя преломления получить аналитические выражения для постоянной распространения, фазовой и групповой скоростей и выяснить зависимость переносимой модой мощности от волноводного параметра в случае одномодового режима. Отметим также, что из всех градиентных профилей оптимальным является квадратичный (см. напр., монографию [20] – при этом профиле разброс нормированных групповых времен пробега разных мод минимален).

• 1.    Явный вид для постоянной распространения в общем виде для градиентного и гауссова профилей

Напряженность электромагнитного поля, распространяющегося вдоль оси z волоконного световода, имеет вид:

E ( t , J? ) - n z exp { - i ( o t -P z ) } E ( r ) ,                  (1)

где n z , ю, в — соответственно единичный вектор вдоль направления распространения волны (ось z ), угловая частота и постоянная распространения (рассматриваем электрическую составляющую – для магнитной составляющей аналогично), R = ( x , y , z ) - координаты, t - время, r = у/x ² + у ² . Таким образом, ось z направлена вдоль оси волновода с круглым поперечным сечением волновода, в котором введены декартовы координаты x , y и полярные координаты r , φ, которые вместе с z являются и цилиндрическими (схематическое изображение на рис. 1). Знак плюс в центре рис. 1 а указывает на то, что ось z перпендикулярна плоскости и направлена к нам.

Из (1) для фазовой скорости uφ находим ot -Рz = const ^ d- (ot -Pz dz dz=OP.(2)

dt

Из уравнений Максвелла с учетом (1) для напряженности поля E ( r ) без учета поляризации легко получить скалярное уравнение для одномодового режима:

d 2 E { r ) + 1 dE^r ) + k ² n ² ,x-ря _E.x ₌ o, dr ²      r dr            ^{( )         ( )}

где n ( r ) – профиль показателя преломления, c – скорость света, k = o /c . Умножая уравнение на rE ( r ) и интегрируя по r от 0 до ∞, получаем

, . d ² E ( r )      , ddE ( r )

'E (r)         + E (r)        + k2 n2 (r) rE2 (r )- dr2           dr

-р ² rE ² ( r )

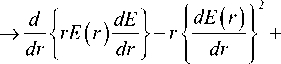
+ k ² n ² ( r ) E ² ( r ) = P ² rE ² ( r ) .

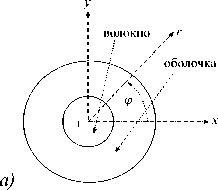
Рис. 1. Схематический вид световода и профиля: а) поперечное сечение световода; б) профиль градиентного

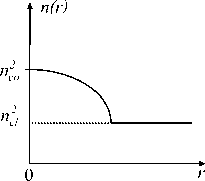
показателя преломления

Здесь учитываем, что поле вместе с производной поля по r на бесконечности обращается в нуль в2 -

M                    M k2 J n2 (r) E2 (r) rdr - j

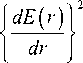
rdr

M

J E ² ( r ) rdr

Рассмотрим показатель преломления, который для произвольного градиентного световода обычно записывается в виде:

2 I \ [ n o f ^{1 - 2 A f} ( r ) ] ’ r -P , n gr ^{( r )-}L^{L        J} ^

I ⁿ cl , ^r >P ,

( \ l ^ ^{-     f} M ’ ^ ^{- 1}

( y )^- i       ^{k 2} p ²

I n ² , Y> 1,

Y = r /p , 0 ,

I ^{f ( r} 1.0 = 0 1 [ f <0 - 0 1

1                                                       I , 1                                                       I , l f ( r )l, -P- if I f (<-11

v - kpEE-?,, a- no-n где nco – значение показателя преломления в сердцевине волокна, ncl – значение показателя преломления в оболочке волокна, ρ – радиус волокна, f (r) – возрастающая на промежутке от 0 до ρ функция, V – волноводный параметр, Δ – высота профиля показателя преломления. Мы остановимся на треугольном, квад-      Подставляя (4) в (3), запишем (β ≡ βgr, E(γ) ≡ Egr(γ)

ратичном и кубическом профилях.                     для профиля (4)):

^в gr P 2 = ;---- ¹----- ] k ² P ² nGo J E gr ( Y ) Y d Y + k ² P ² n d J El ( Y ) Y ^d Y ~ V ² J E g ( Y ) f ( Y ) Y ^d Y - J ^{[ dE} gr ( Y )/ ^d Y ] 2 Y ^d Y L     ⁽⁵⁾

J >■ ( Y ) Y d Y L 0      10°

Наряду с вышеупомянутыми профилями, рассмотрим также и гауссов профиль показателя преломления

J a _gr = 0,16 V ² , 0 <  V <  2,405, [ a g = V - 1,   1 <  V <  2,592

n G ( r ) = n o { 1 - 2 Д ^[ 1 - exp ( -Y ² ) ] } .                 (6)

Форму этого профиля определяет характерный размер ρ . Такая форма профиля – хорошее приближение в случае, когда в процессе изготовления волокна происходит взаимная диффузия материалов сердцевины и оболочки. Подставляя (6) в (3), для гауссова профиля получим (β ≡ β G , E (γ) ≡ E G (γ) для профиля (6)):

в G P ² _----¹----1^Д^ V ² J E G ( Y ) Y d Y +

J E G ( у ) у d y ^{L             0}

■XI                                                             XI

+ V ² J E G ( Y ) exp ( - Y ² ) Y d Y - J

dE G ( Y ) ]²     '

--— y d Y d y

Для профилей (4), (6) поле слабонаправляющего одномодового световода хорошо аппроксимируется гауссовой функцией ( r 0 – радиус модового пятна):

E ( r ) = exp

^ <

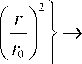
E _gr ( Y ) = exp f-     1 , a gr - ^,

I ² J           r OC gr )

i \ f ^a g Y ² ^           P ²

E G ( Y ) = exp II , ^a G ^- — • I ² J           r O² G )

Подставляя (8) в (5) и (7), получаем

i2 r p ² _| k ² p ² n O

V L VL л

-A- , 2 Д J 2 Д

(α G : для гауссова профиля размер модового пятна r 0 = p /( V 1) '2 > V >1).

2. Постоянная распространения и фазовая скорость для степенного и гауссова профилей

В случае степенного профиля согласно (9) имеем:

I n ( у ) - J exp ( - a gr y² ) Y ^{n + 1} d Y.                       (12)

Для первых трех степеней с учетом (11) из (12) последовательно получим

Ф ( x ) -     J exp ( - 1 ² ) dt -

π 0

интеграл вероятностей:

• -    для треугольного профиля n = 1→ f (γ)= γ:

e 2 r ( 1 ) P ^{2 =} 2 Д { V ² - 2 Д [ 0,16 V ² + 2,22 V Ф ( 0,4 V ) ] } ,

• -    для квадратичного профиля n = 1→ f (γ)= γ²:

в gr ( 2 ) P ² = ^( ^{V 2} - ²^^{0,16 V 2} +

+ 6,25 [ 1 - exp ( - 0,16 V ² ) ] } ) ,

• -    для кубического профиля n = 1→ f (γ)= γ³:

e j r ( 3 > P’ = ^{ V ¹ - ^{2 Д} [ ^{0,16 V 1} -

• - 9,37exp ( - 0,16 V ¹) + ^ V ⁷⁷ ф ( 0,4 V ) ,

A - { 1 - 2 Д[ exp ( -a _gr ) + a _gr/ V ² + 2 a _gr I ( a _gr ) ] } , (9)

I ( a gr ) - J exp ( -a gr у ² ) f ( у ) у d у 0

и 22

в G P ^{2 =} V T - V - 2 Д ( a g + 1 )

Для рассматриваемого слабонаправляющего одномодового световода параметры α gr , α G в (8) следующие (см., напр., [21–23]):

- для гауссова профиля:

в G P ^{2 =} 2 Д^ ² - 2 Д [ 2 V - 1 ] } -

Для фазовой скорости u φ при произвольном профиле с постоянной распространения β в соответствии с (2) запишем:

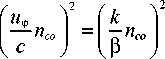
nl k ² p ² ( NA ) ² _ V ²

( NA ) ² в ² Р ^{2     _} 2 Д в ² Р ²

(здесь NA - числовая апертура, NA = у/n ’o - n^- ).

Для ранее рассмотренных случаев находим:

• -    для треугольного профиля

u ( 1 )

= V . ( n _co )^{- 1} - { V ² - 2 Д [ 0,16 V ² +

^{- 1/2}

+ 2,22 V Ф ( 0,4 V ) ] }    ,

• -    для квадратичного профиля:

u ( ² )

= V - ( n co ) 1 - { V ² - 2 Д[ 0,16 V ² +

+ 6,25 ( 1 - exp ( - 0,16 V ² ) ) ] } ^1/2 ,

• -    для кубического профиля

u ( ^{3 )}

= V - ( n co Г1 - { V ² - 2 Д [ 0,16 V ² -

- 9,37exp ( - 0,16 V ² ) + - V ⁷ Ф ( 0,4 V )

- 1/2

.

Для гауссова профиля согласно (10), (11) и (14)

находим:

PGp2 _ 1 + V- - 2V ч 2Д ч u ф( G)  __________V__________ c    nco{V2 -2Д(2V- 1)}V2'

- для треугольного профиля

nco u grup (1) c

3. Групповая скорость для степенного и гауссова профилей. Мощность, переносимая модой

Фазовая скорость определяет скорость распространения фазы вдоль волоконного световода. Мощность же моды переносится вдоль волновода с групповой скоростью. Если фазовая скорость определяется как u φ = ω /β, то групповая скорость определяется как U grup = ∂ω / ∂ β. Для групповой скорости U grup при произвольном профиле с постоянной распространения β запишем вспомогательное соотношение:

Э ( в ² Р ² ) _     ₂ Э р _ Э ( в ² Р ² ) 3 V _

Э k      ^вр Э k    Э V  Э k

Э ( в ² р ² )              Э ( в ² р ² )

^_        P ^{NA _} n co       P^{V 2 Д 4}

3 V             3 V ч Ugru _ f^P cI _  ^IeI     .

c    [Э ю n co V2 Д { Э ( в ² р ²)/ Э V }

С помощью вычисления

d ф( 0,4 V )    2 d f ⁰’4 ^V    , _n J

_—exp(-12)dt dV    Jd dVR 7 I

_ , exp ( - 0,16 V ² )

4 л

d ( 0,4 V ) dV

_ 0,451exp ( - 0,16 V ² )

для всех рассматриваемых случаев аналогично (14 – 17) для групповой скорости согласно (18) получаем:

{ V ² - 2 Д [ 0,16 V ² + 2,22 V -Ф ( 0,4 V ) ] } 1’

V -Д [ 0,32 V + 2,22 Ф ( 0,4 V ) + V exp ( - 0,16 V ² ) ] ’

0 <  V <  2,405;

- для квадратичного профиля

n    { V ² - 2 Д[ 0,16 V ² + 6,25 ( 1 - exp ( - 0,16 V ² ) ) ]р

U grup ^{( 2 )} c           V { 1 - 2 Д[ 0,16 + exp ( - 0,16 V ² ) ] }

0 <  V <  2,405;

- для кубического профиля

- 2 Д

n co

U grup ( 3 ) c

0,16 V ² - 9,37exp ( - 0,16 V ² ) + V Ф ( 0,4 V )

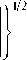
V - 2 Д 0,16 V + 1 1,5 V + 4,^ 1 exp (- 0,16 V ² ) - V ⁴ Ф ( 0,4 V )

- для гауссова профиля:

„ no {V 2 - 2Д( W -I)}’’ grup(G> c           (V - 2Д)

1 <  V <  2,592.

С другой стороны, групповая скорость равна:

P .

mod

^{U grup _} ЙГ' W tot

0 <  V <  2,405;

где P mod , W tot – соответственно мощность, переносимая модой, и полная запасенная энергия на единице длины волновода. Таким образом, можно построить зависимость безразмерной величины η (характеризу-

ющей мощность переносимой моды с точностью до несущественного множителя n co / c ) от волноводного параметра V :

• n co n co ^P mod

• ¹1 grup ¹1 grup (^F ) grup ⁷ ccW tot

71 grup ( 1 ) =1 1 ( V ) , 1 grup ( 2 ) =1 2 ( V ) , ⁽²³⁾ 1 grup ( 3 ) =1 3 ( V ) , 1 grup ( G ) =1 G ( V )

(поскольку U grup / c < 1, а n co > 1, то величина (19) может быть больше единицы). На практике 0,003 < Δ < 0,03, а для конкретных расчетов по формулам (19) – (22) и (23) выберем значение Δ = 0,008, соответствующее часто применяемому значению числовой апертуры NA ≈ 0,13. Согласовывая область значений для волноводного параметра из (19)–(21) с областью из (22), для расчетов определим общую область значений для волноводного параметра 1 <  V <2,405.

Численные расчеты по формулам (19) – (22) дают следующую графическую зависимость параметра η от волноводного параметра V (рис. 2).

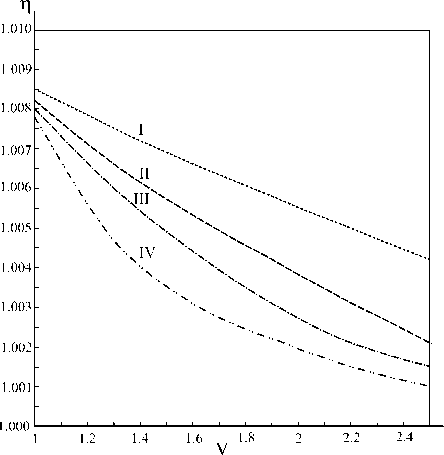
Рис. 2. Линия I – треугольный профиль (η 1 ), линия II – квадратичный профиль (η 2 ), линия III – кубический профиль (η 3 ), линия IV – гауссов профиль (η G )

Заключение

Для круглого в поперечнике слабонаправляющего волоконного световода в одномодовом режиме с произвольным градиентным профилем показателя преломления получено аналитическое выражение для постоянной распространения в общем виде. Для степенного профиля (первые три степени) и гауссова профиля получены зависимости от волноводного параметра для постоянной распространения, фазовой и групповой скоростей. На рис. 2 представлена зависимость групповой скорости, а вместе с ней и мощности, переносимой модой, от волноводного параметра, на примере полученных трёх первых степеней степенного профиля и гауссова профиля. Установлено, что в интервале 1 < V < 2,405 по мере увеличения волноводного параметра и увеличения степени степенного профиля доля переносимой мощности уменьшается и приближается к доле переносимой мощности для гауссова профиля. Этот результат может помочь при выборе режима работы волновода.