Расчет параметров схемы прецизионного позиционирования каналов MDM на торце маломодового волоконного световода
Автор: Бурдин Антон Владимирович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 3 т.14, 2016 года.
Бесплатный доступ
В работе представлена методика расчета параметров схемы прецизионного позиционирования каналов пространственного мультиплексора, реализующего технологию модового уплотнения (MDM - Mode Division Multiplexing), на торце возбуждаемого маломодового оптического волокна (ОВ) линии передачи. Предлагаемое решение базируется на совместном использовании известного метода интеграла перекрытия полей и ранее разработанной модификации приближения Гаусса, обобщенной на случай анализа кварцевых слабонаправляющих ОВ с одной внешней сплошной оболочкой и произвольным осесимметричным профилем показателя преломления. Данный подход позволяет непосредственно перейти к аналитической форме записи выражений для расчета коэффициентов связи мод произвольного порядка с учетом заданного радиального смещения. С помощью представленной методики проведен расчет параметров ввода 5 мод системы MDM в торец маломодового ОВ с диаметром сердцевины 42 мкм и уменьшенной дифференциальной модовой задержкой (ДМЗ). Показано, что при соответствующем сочетании значений радиуса пятна моды канала MDM и радиального рассогласования на вводе удается добиться передачи практически всей мощности вводимой моды MDM отдельной направляемой моде ОВ этого же азимутального порядка. На основании результатов проведенных теоретических расчетов получены практические рекомендации по выбору параметров схемы позиционирования каналов MDM на торце ОВ 42/125 с уменьшенной ДМЗ.
Модовое уплотнение каналов, диаметр пятна моды, маломодовые оптические волокна, оптические волокна с увеличенной эффективной площадью сечения, дифференциальная модовая задержка, прецизионное радиальное смещение, транспортные сети связи нового поколения
Короткий адрес: https://sciup.org/140191835
IDR: 140191835 | УДК: 621.391.63; | DOI: 10.18469/ikt.2016.14.3.04
Текст научной статьи Расчет параметров схемы прецизионного позиционирования каналов MDM на торце маломодового волоконного световода
На сегодняшний день сильное проявление нелинейных эффектов в волоконно-оптических линиях передачи (ВОЛП) является ключевым фактором, ограничивающим реализацию транспортных сетей связи нового поколения, ориентированных на передачу данных со скоростью сотни Тбит/с и выше [1]. Поэтому переход на маломодовые оптические волокна (ОВ) (FMF – Few Mode Fibers) с экстремально увеличенным по сравнению с традиционными телекоммуникационными коммерческими одномодовыми [2] и маломодовыми [3] (ОВ) диаметром сердцевины, обеспечивающим практически полное устранение нелинейности самого волоконного световода, в сочетании с пространственным мультиплексированием (SDM – Space Division Multiplexing) на базе технологий модового уплотнения каналов (MDM – Mode Division Multiplexing) и MIMO (Multiple Input Multiple Output – множественные входы/множественные выходы) является одним из перспективных подходов для решения данной задачи [4 – 7].
Очевидно, что увеличение диаметра сердцевины FMF неизбежно приводит к появлению еще большего числа новых модовых составляющих высших порядков, удовлетворяющих условию отсечки рассматриваемого ОВ. В результате требуется проведение дополнительных мероприятий по уменьшению дифференциальной модовой задержки (ДМЗ) – основного фактора линейных искажений оптического сигнала при распространении по ОВ в маломодовом режиме [8].
Неслучайно при разработке конструкций FMF ключевой проблемой является поиск компромисса между эффективной площадью сечения ОВ, непосредственно связанной с диаметром сердцевины, который, в том числе, определяет модовый состав волоконного световода, и минимизацией ДМЗ на заданной оптической несущей или в определенном выделенном диапазоне длин волн [6-7; 9-10].
В то ж время из теории связи мод хорошо известно [11], что перераспределение мощности оптического сигнала, поступающего с выхода когерентного источника в торец возбуждаемого волоконного световода, осуществляется между ограниченным числом мод этого ОВ, количество и порядок которых определяются геометрией и параметрами возбуждаемого световода, исходным модовым составом (поперечными модами) излучения лазера и непосредственно самими условиями ввода. Так, например, при центрированном вводе, а также вводе с прецизионным радиальным рассогласованием мощность поступающих с выхода источника поперечных мод оптического сигнала передается модам возбуждаемого ОВ только аналогичного азимутального порядка [11, 12]. Безусловно, при дальнейшем распространении сигнала по ОВ ввиду его нерегулярности, а также наличия микро- и макроизгибов, неизбежно возникающих на практике при инсталляции реальных кабельных линий, эта мощность будет также частично передаваться новым модам, но вновь ближайших азимутальных и радиальных порядков [13-15]. Однако если изначально подобрать условия ввода сигнала с выхода лазера в торец волокна таким образом, чтобы практически вся мощность поступаемого излучения передавалась непосредственно одной определенной моде заданного порядка, то и амплитуды новых, возбуждаемых в процессе распространения по ОВ, компонентов будут пренебрежимо малы по сравнению с ней [16-17].
В данной работе предложена методика расчета параметров схемы прецизионного позиционирования каналов пространственного мультиплексора, реализующего технологию MDM, на торце возбуждаемого FMF ВОЛП. На основании представленной методики получены некоторые предварительные результаты теоретического исследования потенциальных возможностей выбора оптимальных параметров передачи вводимых мод и их позиционирования на торце кварцевого FMF с увеличенным диаметром сердцевины 42 мкм, с точки зрения уменьшения ДМЗ за счет передачи мощности вводимого излучения каналов MDM ограниченной группе направляемых мод возбуждаемого ОВ.
Методика расчета коэффициентов связи мод на вводе в ОВ, выполненном с прецизионным радиальным рассогласованием
На сегодняшний день расчет коэффициентов связи по-прежнему остается одним из наиболее известных и простых подходов к анализу перехода оптического излучения от одной моды к другой. Данный метод широко применяется при оценке вносимых потерь и коэффициента отражения на соединении ОВ одинаковой конфигурации с разбросом отдельных технологических параметров – например [12; 18-20] и др., моделировании и исследовании влияния условий ввода оптического излучения на возбуждение оптических волноводов ([11; 21-23] и др.), в том числе и при моделировании распространения оптиче- ских сигналов по ОВ в маломодовом режиме ([8; 13-14; 24-25] и др.).
В общем случае коэффициент связи моды m , возбуждающей моду с индексом n , определяется через интеграл перекрытия полей взаимодействующих мод p и q ( LPlm(p) и LPlm(q) ), который в скалярной постановке задачи для цилиндрической системы координат имеет следующий вид [8; 1114; 18-25]:
_________ о 0
oo 2 7Г oo 2 71 ^
J
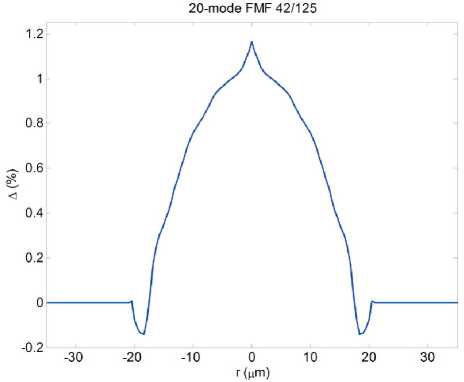
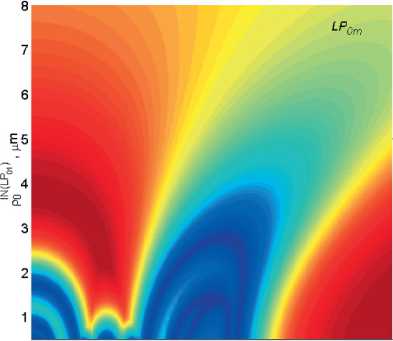
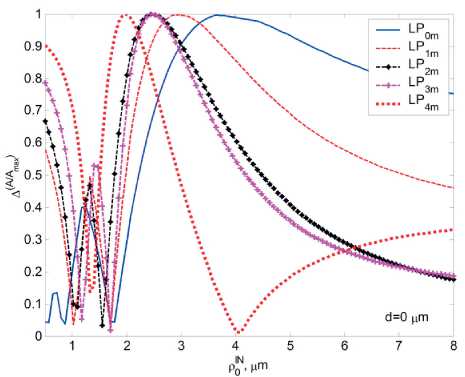
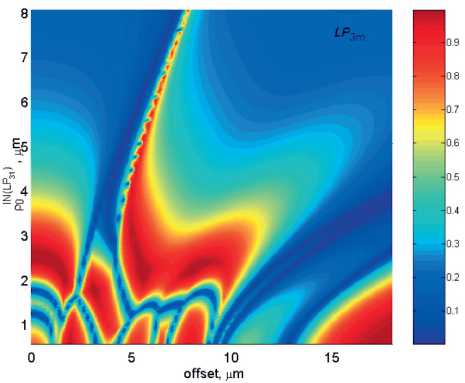
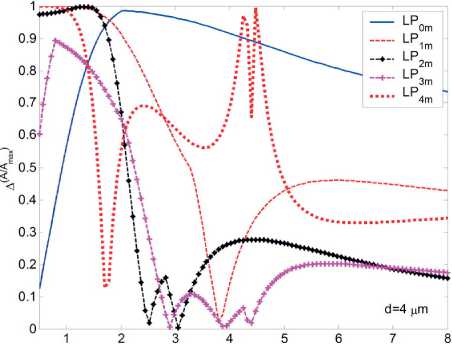
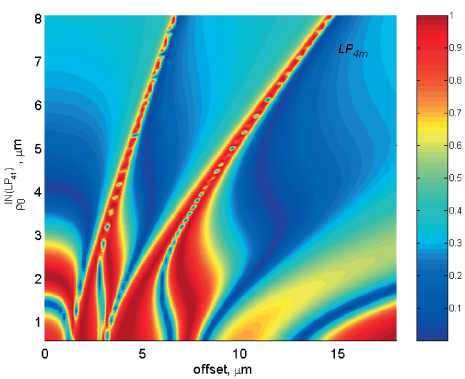
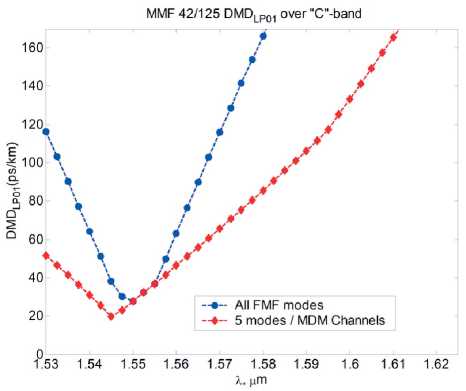
^Fm^^d 0 0 0 0 где F4pи ^,„0) – радиальные распределения полей взаимодействующих – мод поступающей с выхода источника моды LPlm(p) и возбуждаемой в ОВ моды LPlm(q). Очевидно, что наиболее простая структура поля относится к основной моде LP01. Это позволяет перейти непосредственно к аналитической форме записи интеграла перекрытия полей (1), используя, например, для представления поля соответствующие аппроксимирующие выражения или разложение в ряд в базисе заданных функций. Подобный подход активно применяется, например, для анализа стыков одномодовых ОВ, что и отражено в перечисленных выше публикациях – в частности [11; 18-19; 21; 23] и др. Напротив, структура поля высших мод носит более сложный характер. По этой причине в работах, ориентированных на анализ взаимодействия мод высших порядков – например, [8; 24-25] и др., – интеграл числителя выражения (1) предлагается брать численно или использовать простые аппроксимирующие выражения, соответствующие точным решениям волнового уравнения. В частности, в рамках приближения Гаусса [11] для волокон с идеальным неограниченным параболическим профилем показателя преломления, в состав которого входит удобная для интегрирования функция Лагерра-Гаусса: где l и m – азимутальный и радиальные порядки моды LPlm, соответственно; R = r / a – нормированная радиальная координата; r – радиальная координата; a – радиус сердцевины; ^o Po i a – нормированный радиус пятна моды; ро – радиус пятна моды; Дп-\ – полином Лагерра. Однако и в этом случае возникают определенные трудности перехода к аналитическим выражениям для коэффициента связи мод неединичного радиального порядка: при m > 1 в подынтегральном выражении числителя формулы (1) фигурирует произведение полиномов Лагерра разного порядка, что в общем случае не относится к «табличным» интегралам. По этой причине, например, в монографии [11] представлены решения только для основной моды и высших мод первого радиального порядка m = 1 LPl1. Кроме того, представление профиля показателя преломления ОВ с помощью набора простых гладких степенных функций или, тем более, только одной степенной функции – в частности неограниченной параболы – для перехода к описанию распределения поля моды не является корректным как с точки зрения расчета параметров модового состава реальных промышленных образцов ОВ, градиентный профиль показателя преломления которых существенно отличатся от гладких модельных а-профилей [26-27], так и тем более специализированных профилей FMF, обеспечивающих уменьшенную ДМЗ. Для решения описанной проблемы предлагается воспользоваться ранее разработанной модификацией приближения Гаусса (ОМПГ) [15], обобщенной на случай расчета спектральных характеристик дисперсионных параметров направляемых мод произвольного порядка, распространяющихся в слабонаправляющих ОВ с произвольным осесимметричным профилем показателя преломления. Предложенный метод базируется на сочетании приближения Гаусса [11], модифицированного для расчета многомодовых ОВ [15], и методе стратификации [28]. Здесь, в отличие от известных решений, базирующихся на классическом приближении Гаусса [11] и его различных модификациях [29-35], предлагается рассматривать исследуемый слабонаправляющий волоконный световод с произвольным осесимметричным профилем показателя преломле- ния, ограниченным одной внешней сплошной оболочкой, как слабонаправляющий волоконный световод с многослойным профилем показателя преломления, представляемый в области сердцевины ОВ в виде конечного числа N слоев, в пределах которых значение показателя преломления остается постоянным. В результате при задании исходных данных обеспечивается детализированное воспроизведение профиля показателя преломления исследуемого ОВ, что существенно снижает погрешность расчетов [36]. Таким образом, с точки зрения предложенного приближенного метода ОМПГ, подстановку выражения (2), описывающего распределение поля моды, в интеграл перекрытия полей (1) можно полагать корректным. Действительно, ОМПГ использует для представления поля моды заданного порядка простое аппроксимирующее выражение (2), однако при этом учитывается реальная структура профиля исследуемого градиентного ОВ, что и обеспечивает малую погрешность расчетов [36]. Как было отмечено выше, при подстановке обобщенного на произвольный порядок моды аппроксимирующего выражения (2) в интеграл перекрытия полей (1) для высших мод возникают определенные трудности интегрирования числителя (1). В первую очередь это связано с интегралами от произведения полиномов Лагер-ра разной степени и порядка, которые в общем случае не относятся к табличным. В рамках данной работе эта проблема преодолевается путем использования формулы явного представления полинома Лагерра в виде конечного степенного ряда соответствующего вида [37]. Все это позволило получить достаточно громоздкие, содержащие несколько конечных вложенных сумм, но при этом аналитические формулы для оценки коэффициентов связи мод произвольного порядка на стыке двух слабонаправляющих ОВ с неодинаковыми параметрами, выполненном с осевым смещением. В результате обобщенное аналитическое выражение для коэффициентов связи мод LPlm и LPln произвольного порядка на стыке ОВ с осевым смещением d будет иметь вид: где ^РтР^, (Р™ + Р^ ехр 1 m+n-2 min(p.m-l) p min(s,) 7+2(—r) 2 J 4(,'=|z Z ь;-'!,^^ Ее,'"--'Zn?'Z^i; ^ p=0 q=max(O,p-n+l) .s-0 Z=max(0,5-/?+^) k=0 w=0 J-U+PS-wl 211 (и +1 - 2w)! w! 2^s-q+w^-l 2(s-p+q+u-w)+l m г n ( 2 J m+n-2 min(p,m-l) p+p+A min(s^+//+l) /+2(^-/) мЧ'-^р^ Z ьр-''bp"^ Ze- ”'Zfilz| Z^'1; p=0 p-0 q^max^O,?-»^ ^=0 f=max(0,s-/?+^) k=0w=0 („ =(-ir / y-p-iy. . A 22a+3p + 1 [/-2(^ + 1)]!^! ’ V 2 J m+n-l min(p,m-l) p+p+\ min(s,<7) l+2^q-t^\ 2 J Ml' = Z PS’ Z Z C'_,’6!X_"Z Ze<,‘""*" Zfi!'* Z41.!'1: p=0 p=0 q=max(0,p-n+\^ s=0 t=max(0>.s-p+q-p-V) k=0w=0 k=0 w=0 ^11."Л – соответствующие коэффициенты степенного ряда формулы явного выражения полинома Лагерра^m(XY Для перехода от эквивалентных, полученных в результате расчета на основании ОМПГ, значений радиусов пятна моды к фактическим предлагается воспользоваться хорошо известной интегральной формой записи формулы поправки Петерманна-2 для радиуса пятна моды в ближнем поле (MFR^;2) [39], которое в результате соответствующих преобразований после подстановки аппроксимирующего выражения для радиального распределения поля моды (2) приводится к аналитической формуле (4). Таким образом, методика расчета коэффициентов связи поперечных мод оптического из- лучения, поступающих с выхода портов MDM-мультиплексора, на торец FMF ВОЛП включает в себя следующие этапы. Предварительно задается профиль показателя преломления и базовые геометрические параметры исследуемого ОВ. Далее с помощью ОМПГ осуществляется расчет эквивалентных, в рамках приближения Гаусса, значений радиусов пятна мод модового состава FMF. Затем выполняется переход от эквивалентных к фактическим значениям радиусов пятна мод с использованием выражения для поправки Петерманна-2 (4). После чего для оценки коэффициента связи в формулу (3) осуществляется подстановка полученных значений радиусов пятна моды соответствующего порядка FMF этого же параметра соответствующей поперечной моды излучения канала MDM и непосредственно самого прецизионного радиального смещения ввода этой моды относительно центра сердцевины исследуемого ОВ. Результаты расчетов: выбор оптимальных параметров схемы прецизионного позиционирования каналов MDM на торце FMF 42/125 В качестве примера в данном разделе представлены результаты анализа распределения коэффициентов связи мод FMF соответствующих азимутальных порядков в заивисимости от комбинации радиуса пятна моды первого радиального порядка LPl1 излучения канала MDM и прецизионного радиального смещения ввода d этой моды относительно центра сердцевины возбуждаемого ОВ. Рис. 1. Градиентный профиль показателя преломления FMF 42/125 с уменьшенной ДМЗ Рассматривается кварцевое слабонаправляющее FMF с диаметром сердцевины 42 мкм и оболочкой 125 мкм. Данное ОВ поддерживает распространение до 20 направляемых мод LPlm – до шестого азимутального l = 0…6 и четвертого радиального m = 1…4 порядков включительно в «С»-диапазоне длин волн. Полученный в результате оптимизиции специализированный профиль показателя преломления, внешний вид которого приведен на рис. 1, обеспечивает значение ДМЗ относительно основной моды менее 30 пс/км на оптической несущей X = 1550 нм. Предполагается, что при определенной комбинации радиуса пятна моды LPl1 соответствующего канала MDM и ее положения на торце, смещенного относительно центра сердцевины возбуждаемого ОВ, можно добиться передачи практически всей ее мощности одной определенной моде FMF этого же азимутального порядка. Для проверки данной гипотезы на основании представленной методики анализа ввода оптического излучения каналов MDM в торец ОВ был проведен расчет коэффициентов связи мод FMF и, соответственно, вводимых мод в зависимости от радиуса пятна последних и их положения относительно центра сердцевины возбуждаемого ОВ. На первом этапе предлагается рассмотреть пятиканальную систему MDM, оснащенную мультиплексором, обеспечивающим ввод 5 мод первого радиального порядка LP0m…LP4m. Рассматривался диапазон значений радиуса пятна мод каналов MDM р» = 0,5…8,0 мкм и осевого смещения d = 0,0…18,0 мкм. Полученные результаты расчетов коэффициентов связи позволили перейти к построению диаграмм зависимости минимального разброса нормированных амплитуд возбуждаемых мод FMF в зависимости от перечисленных выше параметров. В качестве примера, на рис. 2 представлены указанные диаграммы для мод нулевого (а), третьего (б) и четвертого (в) азимутальных порядков. Анализ построенных диаграмм позволил выделить две локации торца FMF, соответствующие непосредственно центру сердцевины ОВ d = 0 мкм и ее периферийной части, отстоящей от последнего на расстоянии d = 4 мкм, при которых для всех пяти перечисленных модовых групп LP 0 in-*- LP 4 т минимальное отклонение нормированных амплитуд внутри одной группы идентичного азимутального порядка l = 0…4 достигает значения от 0,85 и более. Далее для указанных локаций были построены кривые зависимости минимального разброса нормированных амплитуд возбуждаемых мод FMF от радиуса пятна вводимой моды LPl1 при фиксированном радиальном смещении d относительно центра ОВ, представленные на рис. 3. Это позволило выделить искомые значения радиуса пятна вводимых мод LPl1 каналов MDM, при которых достигается искомое максимальное отклонение нормированных амплитуд возбуждаемых мод одного азимутального порядка, составляющих более 0,85. А последующее сопоставление распределения расчетных значений коэффициентов связи мод внутри одной группы – определить, какой именно моде передается основная часть мощности сигнала канала MDM LPl1. Далее на основании анализа диаграммы ДМЗ были отобраны оптимальные, с точки зрения минимизации ДМЗ по основной моде LP01, комбинации возбуждаемой моды FMF заданного порядка, IN радиуса пятна вводимой моды канала MDM Ро и ее позиционирования на торце исследуемого ОВ d. О 5 10 15 offset, jim 0.9 0.8 0.7 □.Б 0.5 0.4 0.3 0.2 0.1 (а) (a) Р^- Pm (б) (б) Рис. 2. Диаграмма зависимости минимального разброса нормированных амплитуд возбуждаемых мод FMF в зависимости от радиуса пятна вводимой моды LPn и ес радиального смещения d относительно центра ОВ: (а) моды LPOm\ (б) моды LP3m ; (в) моды LP 4т Рис. 3. Кривые зависимости минимального разброса нормированных амплитуд возбуждаемых мод FMF в зависимости от радиуса пятна вводимой моды LPп при фиксированном радиальном смещении d относительно центра ОВ: (а) центрированный ввод d=0,0 мкм; (б) <^=4,0 мкм Анализ полученных результатов показал следующее: центрированный ввод целесообразно осуществлять для моды LP21, при этом ее радиус пятна моды должен составлять _IN(LP2Y)_^ _______ Ро — L^j мкм. В этом случае практически вся мощность данного канала MDM перейдет моде FMF этого же порядка, при этом минимальный разброс нормированных амплитуд внутри модовой группы ОВ второго азимутального порядка l = 2 составит 0,99. Для остальных четырех мод каналов MDM можно рекомендовать позиционирование в периферийной зоне сердцевины возбуждаемого ОВ на расстоянии d = 4 мкм от центра последней. В этом случае при вводе основ- ной моды LP01 c радиусом пятна ^WL^og мкм в FMF будет также возбуждаться основная мода LP01 нормированная амплитуда которой будет отличаться от аналогичного параметра мод LP0m этой же группы нулевого азимутального порядка l = 0 более чем на 0,99. В свою очередь, ввод моды LP11 канала MDM при p'N^LmM,%% мкм и аналогичном смещении d = 4 мкм от центра сердцевины обеспечит возбуждение моды LP12 с отклонением нормированной амплитуды от мод этой же группы l = 1 более 0,99. В свою очередь, при вводе LP31 с радиусом пятна P^^iUq^ мкм и d = 4 мкм практически вся мощность этой моды переходит компоненте LP32 с отклонением нормированной амплитуды в этой группе l = 3 не менее чем на 0,89. Наконец, для группы мод LP4m ввод LP41 с радиусом пятна p^LP^=O,58 мкм при таком же смещении d = 4 мкм обеспечит возбуждении моды FMF LP42, нормированная амплитуда которой будет превышать остальные компоненты из той группы l = 4 более чем на 0,99. Рис. 4. Спектральные зависимости ДМЗ по основной моде FMF 42/125 в пределах волнового «С»–диапазона без и с подбором параметров схемы позиционирования мод каналов MDM на торце исследуемого ОВ Для оценивания потенциальных возможностей управления ДМЗ модового состава FMF 42/125 за счет выбора соответствующих параметров схемы позиционирования вводимых мод каналов MDM на торце исследуемого ОВ был выполнен расчет спектральных характеристик ДМЗ в «С»-диапазоне длин волн для всех мод рассматриваемого FMF, удовлетворяющих условию отсечки, и 5 возбуждаемых мод (LP01, LP12, LP21, LP32, LP42) при контроле указанных условий ввода. Данные кривые представлены на рис. 4. Анализ полученных результатов показыва- ет, что выбор соответствующей комбинации параметров схемы позиционирования вводимых мод каналов MDM на торце исследуемого FMF 42/125 позволяет уменьшить локальное значение ДМЗ на искомой оптической несущей 1550 нм с 27,70 пс/км до 19,8 пс/км, увеличить на 18,5 нм относительно исходного значения спектральный диапазон центральной области «С»-диапазона, соответствующий пониженным значения ДМЗ по основной моде до 60 пс/км и в целом более чем в два раза уменьшить ее значение за пределами указанной области длин волн. Заключение Представлена методика расчета параметров схемы прецизионного позиционирования каналов MDM на торце возбуждаемого ОВ ВОЛП. Проведен расчет параметров ввода 5 мод низших азимутальных порядков системы MDM в торец FMF с диаметром сердцевины 42 мкм и уменьшенной дифференциальной модовой задержкой (ДМЗ). Показано, что при соответствующем сочетании значений радиуса пятна моды канала MDM и радиального рассогласования на вводе удается добиться передачи практически всей мощности вводимой моды MDM отдельной направляемой моде ОВ этого же азимутального порядка. На основании результатов проведенных теоретических расчетов получены практические рекомендации по выбору параметров схемы позиционирования каналов MDM на торце ОВ 42/125. Продемонстрирована потенциальная возможность снижения ДМЗ в центральной области «С»-диапазона при соответствующем подборе комбинации параметров схемы позиционирования: радиуса пятна вводимой моды канала MDM, ее положения на торце FMF относительно центра сердцевины и порядок возбуждаемой моды ОВ , нормированная амплитуда которой превышает амплитуды остальных мод из этой же группы аналогичного азимутального порядка не менее чем на 0,85. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-60015 мол_а_дк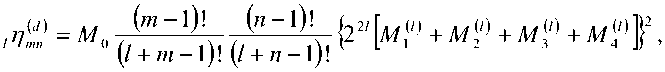
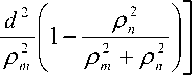
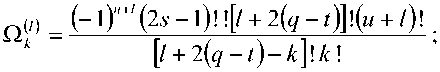
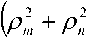
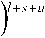
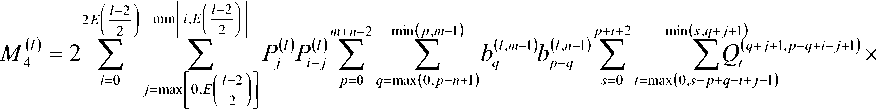
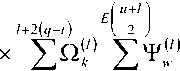
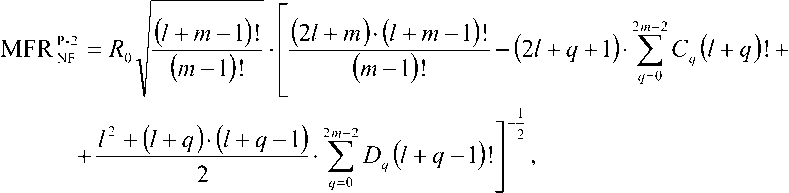

Список литературы Расчет параметров схемы прецизионного позиционирования каналов MDM на торце маломодового волоконного световода
- T. Morioka. Recent progress in space-division multiplexed transmission technologies//OFC/NFOEC Technical Digest. -2013. -OW4F.2. -P. OW4F.2-1 -OW4F.2-4 DOI: 10.1364/OFC.2013.OW4F.2
- Оптические волокна для линий связи/А.В. Листвин, В.Н. Листвин, Д.В. Швырков. -М.: ЛЕСАРарт, 2003. -288 с.
- OFS. Few mode optical fiber series. OFS Fitel LLC. Product catalog, 2016//http://fiber-optic-catalog.ofsoptics.com/viewitems/few-mode-optical-fiber-series/few-mode-optical-fiber-series1
- Kubota H., Morioka T. Few-mode optical fiber for mode-division multiplexing//Optical Fiber Technology. -2011. -vol. 17. -P. 490 -494 DOI: 10.1016/j.yofte.2011.06.011
- Richardson D.J., Fini J.M., Nelson L.E. Space-division multiplexing in optical fibers//Nature Photonics. -2013. -V. 7, No 5. -P. 354 -362 DOI: 10.1038/nphoton.2013.94
- Mizuno T., Takara H., Sano A., Miyamoto Yu. Dense space-division multiplexed transmission systems using multi-core and multi-mode fiber//IEEE Journal of Lightwave Technologies. -2016. -vol. 34(2). -P. 582 -592.
- Stillard P., Molin D., Bigot-Astruc M., Amezcua-Correa A., de Jongh K., Achten F. 50 mm multimode fibers for mode division multiplexing//IEEE Journal of Lightwave Technologies. -2016. -vol. 34(8). -P. 1672 -1677.
- Bottacchi S. Multi-Gigabit transmission over multimode optical fibre. Theory and design methods for 10GbE systems. West Sussex: John Wiley & Sons Ltd., 2006. -654 p.
- Ferreira F.M., Fonseca D., da Silva H.J.A. Design of few-mode fibers with M-modes and low differential mode delay//IEEE Journal of Lightwave Technology. -2014. -32(3). -P. 353 -360.
- Stillard P. Next-generation fibers for space-division-multiplexed transmission//IEEE Journal of Lightwave Technologies. -2015. -vol. 33(5). -P. 1092 -1099.
- Snyder A.W., Love J. Optical waveguide theory, Chapman & Hall, 1983. -738 p.
- Срапионов В.А. Связь мод в стыках оптических волокон с разбросом параметров//Электросвязь. -1985. -№10. -стр. 10 -12.
- Gholami A., Molin D., Sillard P. Physical modeling of 10 GbE optical communication systems//IEEE Journal of Lightwave Technology. -2011. -vol. 29(1). -P. 115 -123.
- Pepeljugoski P., Golowich S.E., Ritger A.J., Kolesar P., Ristetski A. Modeling and simulation of next-generation multimode fiber links//IEEE Journal of Lightwave Technology. -2003. -vol. 21(5). -P. 1242 -1255.
- Bourdine A. Modeling and simulation of piecewise regular multimode fiber links operating in a few-mode regime//Advances in Optical Technologies. -2013. -vol. 2013. -P. 469389-1 -469389-18 DOI: 10.1155/2013/469389
- Bunge C.-A., Choi S., Oh K. Analysis of ring launching scheme using hollow optical fibre mode converter for 10 Gps multimode fibre communication//Optical Fiber Technology. -2006. -vol. 12. -P. 48 -58 DOI: 10.1016/j.yofte.2005.05.001
- Sim D.H., Takushima Y., Chung Y.C. High-speed multimode fiber transmission by using mode-field matched center-launching technique//IEEE Journal of Lightwave Technology. -2009. -vol. 27(8). -P. 1018 -1026.
- Гурджи С.П., Каток В.Б. Расчет потерь в соединениях одномодовых световодов со сложным профилем показателя преломления//Электросвязь. -1990. -№10. -С. 25 -27.
- Meunier J.P., Hosain S.I. An accurate splice loss analysis for single-mode graded-index fibers with mismatched parameters//IEEE Journal of Lightwave Technology. -1992. -vol. 10(11). -P. 1521 -1526.
- Yu Q., Zongo P.-H., Facq P. Refractive index profile influences on mode coupling effects at optical fiber splices and connectors//IEEE Journal of Lightwave Technology. -1993. -vol. 11(8). -P. 1270 -1273.
- Chandra R., Thyagarajan K., Ghatak A.K. Mode excitation by tilted and offset Gaussian beams in W-type fibers//Applied Optics. -1978. -vol. 17(17). -P. 2842 -2847 DOI: 10.1364/AO.17.002842
- Авруцкий И.А, Сычугов В.А., Тищенко А.В. Исследование процессов возбуждения, излучения и отражения света в гофрированных волноводах//Труды ИОФАН. -1991. -Т. 34. -С. 3 -98.
- Hosain S.I., Meunier J.P., Wang Z.H. Coupling efficiency of butt-joined planar waveguides with simultaneous tilt and transverse offset//IEEE Journal of Lightwave Technology. -1996. -vol. 14(5). -P. 901 -907.
- Raddatz L., White I.H., Cunningham D.G., Nowell M.C. An experimental and theoretical study of the offset launch technique for the enhancement of the bandwidth of multimode fiber links//IEEE Journal of Lightwave Technology. -1998. -vol. 16(3). -P. 324 -331.
- Webster M., Raddatz L., White I.H., Cunningham D.G. A statistical analysis of conditioned launch for Gigabit Ethernet links using multimode fiber//IEEE Journal of Lightwave Technology. -1999. -vol. 17(9). -P. 1532 -1541.
- Бурдин А.В., Яблочкин К.А. Исследование дефектов профиля показателя преломления многомодовых оптических волокон кабелей связи//Инфокоммуникационные технологии. -2010. -№2. -С. 22 -27.
- Bourdine A.V., Praporshchikov D.E., Yablochkin K.A. Investigation of defects of refractive index profile of silica graded-index multimode fibers//Proceedings of SPIE. -2011. -vol. 7992. -P. 799206-1 -799206-6 DOI: 10.1117/12.887258
- Adams M.J. An introduction to optical waveguides. New York: John Wiley and Sons, 1981. -401 p.
- Meher H., Hosain S.I. Variational approximations for single-mode graded-index fibers: some interesting applications//Journal of Optical Communications. -2003. -vol. 24(1). -P. 25 -30 DOI: 10.1515/JOC.2003.24.1.25
- Sharma A., Hosain S.I., Ghatak A.K. The fundamental mode of graded-index fibres: simple and accurate variational methods//Optical and Quantum Electronics. -1982. -vol. 14(1). -P. 7 -15 DOI: 10.1007/BF00620905
- Tewari R., Hosain S.I., Thyagarajan K. Scalar variational analysis of single mode fibers with Gaussian and smoothed-out profiles//Optics Communications. -1983. -vol. 48(3). -P. 176 -180.
- Oksanen M.I., Lindell I.V. Variational analysis of anisotropic graded-index optical fibers//IEEE Journal of Lightwave Technology. -1989. -vol. 7(1). -P. 87 -91.
- Ankiewicz A., Peng G.-D. Generalized Gaussian approximation for single-mode fibers//IEEE Journal of Lightwave Technology. -1992. -vol. 10(1). -P. 22 -27.
- Holmes M.J., Spirit D.M., Payne F.P. New Gaussian-based approximation for modeling non-linear effects in optical fibers//IEEE Journal of Lightwave Technology. -1994. -vol. 12(2). -P. 193 -201
- Wu M.-Sh., Lee M.-H., Tsai W.-H. Variational analysis of single-mode graded-core W-fibers//IEEE Journal of Lightwave Technology. -1996. -vol. 14(1). -P. 121 -125.
- Bourdine A.V., Delmukhametov O.R. Calculation of transmission parameters of the launched higher-order modes based on the combination of a modified Gaussian approximation and a finite element method//Telecommunications and Radio Engineering. -2013. -vol. 72(2). -P. 111 -123 DOI: 10.1615/TelecomRadEng.v72.i2.30
- Градштейн И.С., Рыжик И.М. Таблицы интегралов. -М.: Физматгиз, 1962. -1100 с.
- Definition and test methods for the relevant parameters of single-mode fibres. ITU COM 15-273-E. 1996.
- Dubois F., Emplit Ph., Hugon O. Selective mode excitation in graded-index multimode fiber by a computer-generated optical mask//Optics Letters. -1994. -vol. 19(7). -P. 433 -435 DOI: 10.1364/OL.19.000433
- Karpeev S.V., Pavelyev V.S., Soifer V.A., Doskolovich L.L., Duparre M., Luedge B. Mode multiplexing by diffractive optical elements in optical telecommunication//Proceedings of SPIE. -2004. -vol. 5480. -P. 163 -165 DOI: 10.1117/12.558775
- Noordegraaf D., Skovgaard P.M., Nielsen M.D., Bland-Hawthorn J. Efficient multi-mode to single-mode coupling in a photonic lantern//Optics Express. -2009. -vol. 17(3). -P. 1988 -1994 DOI: 10.1364/OE.17.001988
- Leon-Saval S.G., Argyros A., Bland-Hawthorn J. Photonic lanterns: a study of light propagation in multimode to single-mode converters//Optics Express. -2010. -vol. 18(8). -P. 8430 -8439 DOI: 10.1364/OE.18.008430


