Расчет параметров структуры и энтальпии образования хромишпинелей

Хромшпинелиды, представляющие собой минералы переменного состава группы шпинели 2-3 (МеО-Ме2О3), являются главными промышленными минералами хромовых руд [1,2]. Близость кристаллохимических свойств катиона Сг3+ и свойств катионов Feo+ и А13+определяет возможность широкого изоморфного замещения трехзарядных катионов. Кроме того, близость свойств и возможность широкого изоморфного замещения двухзарядных катионов Mg2+ и Ре2+ , присутствующих чаще других в промышленных рудах хрома, а также возможность окисления двухзарядного катиона железа до трехзарядного с последующим замещением части катионов хрома делают состав природных шпинелидов весьма разнообразным. Изменение состава соединения влечет за собой изменение свойств, в том числе важных с технологической точки зрения. В частности, термодинамическую устойчивость соединения характеризует энтальпия его образования, и чем боле отрицательна энтальпия образования, тем устойчивее соединение и тем больше энергии необходимо затратить на восстановление металлов из этого соединения. Исследовать экспериментально структурные и термохимические свойства хромшпинелидов всей гаммы возможных составов представляется чрезвычайно большой и трудновыполнимой задачей. До сих пор отсутствуют и расчетные методы определения структурных и термохимических констант соединений переменного состава, какими являются природные хромшпинелиды.

Разработанная и использованная ранее [3-5] для определения структурных и термохимических констант низших оксидов алюминия математическая модель расчета позволяет определять эффективные радиусы простых и сложных ионов, нейтральных аддендов, структурных фрагментов, параметров кристаллических решеток соединений, формирующихся в кубической сингонии, а также энтальпию их образования. В модели принято и обосновано деление сложных веществ на фрагменты. В частности, нормальные оксидные шпинели типа 2-3 представляются в виде Ме2+[Мео+2О4]. В случае комплексных шпинелей, в частности хромшпинелидов, образованных катионами нескольких металлов, нормальные шпинели можно представить в виде Me/Me/n[MexIIIMe/vCrzO4]. В соответствии с принятой в химии комплексных соединений практикой компоненты, заключенные в скобки [ ], рассматриваются как составляющие внутреннюю сферу, а находящиеся за этими скобками - как компоненты внешней сферы.

Согласно разработанной модели межструктурное расстояние гр (расстояние между центрами фрагментов шпинели) определяется по формуле гр = ad,                                     (1)

где а - геометрический фактор, который включает в себя структурные константы, характерные для октаэдрической (1/4) и тетраэдрической( 8/зТз ) структур, d - параметр кристаллической решетки.

С учетом этих величин г = — —• d = 0,3849 • d, ^Р 4 3^3

откуда d = r_? /0,3849.

Чтобы рассчитать межструктурное расстояние гр, сначала по формуле

/        _\ о

г[} = г^ +

I и         __у          I . У

\ ОМе^ DMe„2* / Ф»>  \ О2" / необходимо определить размер внутренней сферы Г[ ]. В этой формуле г - средний радиус катионов во внутренней сфере г

г°2_ - минимальный радиус аниона О2 = 1,35806 А, гКи и гп„ - дебаевские радиусы экранирования иона внутренней сферы и наружного катиона. Для нормальной шпинели со структурой сфалерита ZnS радиус экранирования наружного иона Ме2+ г„ =    -3V2 = 17,581767 -3^2 = 74,59312 А, а внутреннего гю„ = г^ • 2(1 + V3) = 17,581767 ■ 2(1 + V3) =

= 96,06856 A.

После определения г( рассчитываем

Г=Р„ = ^ +Ле2»

(здесь гср - средний радиус катиона во внешней сфере) и по уравнению

ОМе 2+ Ф= [ 1

^ = Г Н---------------

находим межструктурное расстояние, а затем и параметр решетки.

Результаты расчета геометрических констант, в свою очередь, позволяют оценить энтальпию образования кристаллических оксидов и энтальпию их кристаллических решеток.

По определению энергия (энтальпия) кристаллической решетки представляет собой разность энтальпии образования газообразных ионов компонентов с соответствующими коэффициентами и энтальпии образования химического соединения в кристаллическом виде

Ар^(Ме_пА_т) = п- AXCMe”^) + т- A_/rf(A'"_T) -

-Ду^МеЛшкр).                    (4)

Энтальпии образования газообразных ионов определены с известной точностью. Поэтому для определения энтальпии образования кристаллического соединения - Д/^Ме^т^,) требуется найти энтальпию кристаллической решетки.

Согласно [3] энтальпию кристаллической решетки можно представить в виде суммы двух слагаемых

АрН(Ме_хАу) = АН₀ + АН_Ю.               (5)

Здесь АЯ0 - энтальпия нулевого уровня, от которого идет отсчет. Величина Айо постоянна для данного типа кристаллической структуры, зарядов частиц и их электронного строения. ДЯВЗ - энтальпия взаимодействия, учитывающая взаимодействие частиц, которое зависит от величины их зарядов, строения и определяет структуру кристаллической решетки.

Примем, что отсчет ведется от простейших атомов водорода. Тогда [4]

AH0=N,—10s-10-3-./;(Z), где Na = 6,022045T02j моль"1 - число Авогадро, е = 4,803242-10"10 CGSE (г1/2см3/2с"1), 108 и 10"3 -численные коэффициенты перевода единиц в систему СИ, «о = 0,52912-10"8 см - боровский радиус атома водорода, /i(Z) - функция структуры и заряда (включает в себя произведение Z^ -Z2).

^H^=Na-— ^108-10-3-/2 (z), где Ам - число Маделунга (для структуры ZnS Ам =1,63806),/2(Z) - функция структуры и заряда (включает в себя произведение

-ifz-'4t^Jкч'

где КЧ - координационное число). Для шпинелей, включающих ^-элементы, после подстановки чис ленных величин получим

АЯ° (Ме„А„) = 114,1741 (2-3)2 +

1087,4125

Г,              U + 1J

= 4110,268 +

49670,9255

АХ(Ме^и) = zAy//°(Mg2+r) +;AX(Fe2+r) +

+ xAX(Fe³⁺_r) +yAX(Al³⁺r) + z ^(С?\) +

+ 4Дг^(О²-_г) - АХ(Ме_иА» кр), (7) находим энтальпию образования кристаллической хромишпинели.

Таким образом, для проведения расчетов по изложенной методике необходимо знать ионные радиусы и энтальпию образования ионов элементов, входящих в состав шпинели. Ионные радиусы компонентов и энтальпия образования иона О2" определены ранее [3, 4], энтальпию образования остальных ионов заимствовали из литературы [6,7]:

Ионы Радиус, А -АуЯ°, кДж/моль	Mg2+ 0,71864 2347,235	Or 0,70102 5634,978	Fe2" 0,75152 2946,662
Ионы	Fe3+	Al3"	О2"
Радиус, А	0,72510	0,58917	1,35806
-АН0, кДж/моль	5703,913	5473,387	1069,128

В качестве примера в таблице приведены результаты расчета параметров структуры и энтальпии образования нормальной шпинели (Mg,²''Fe/")[(Fe/⁺Al_v³⁺CrA)2O₄^ при значениях / = 1 и у = 0. Значения параметров х, у и z в расчетах изменяли таким образом, чтобы составы располагались по сечениям треугольника Fe³⁺-Al³⁺- Сг³⁺ вдоль линий Fe³⁺-B, А1³⁺- А и Cr³⁺- С (рис. 1).

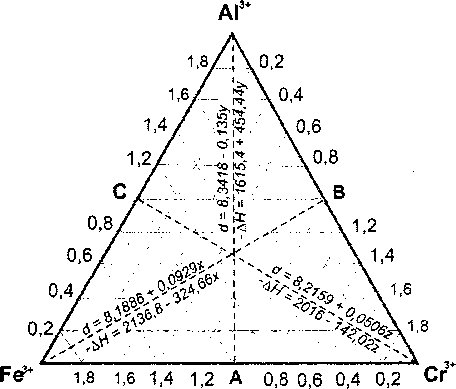
Рис. 1. Составы шпинели Mg2t[(Fe/*Aly3*Cr/+)2O4], для которых в таблице приведен расчет структурных и термохимических констант, и уравнения параметра решетки и энтальпии образования кристаллической шпинели соответствующего состава

Из результатов расчета следует, что вдоль каждого из выбранных сечений треугольника составов параметр кристаллической решетки и энтальпия образования шпинели изменяются по линейному закону, хотя уравнения (2) и (3) не являются строго линейными. Вместе с тем, математический анализ показал, что изменение структурных и термических характеристик при изменении состава

Результаты расчета параметров структуры и энергии образования магнохромишпинели состава Mg[Fe,AlyCrzO4]

	Mg[FexAlvCr2O4]	rP A	a A	^V-^fras) ■	^nH 1	^fH (шпинели)
Система магнохромпикатитит - магноферрихромпикатит - магноферрит (линия В -Fe3+)
1	Mg[Fe0 Al i,oCrLo04]	3,15245	8,19031	17732,11	19866,55	2134,44
2	Mg[Fe0 05 А1о,975СГо,97504]	3,15411	8,19462	17739,59	19858,25	2118,65
3	Mg[Fe01 Alo.95Cro.95O4]	3,15578	8,19896	17747,08	19849,92	2102,84
4	Mg[Fe02 Alo.9Cro.9O4]	3,15914	8,20769	17762,05	19833,19	2071,13
5	Mg[Fe0 3 Alo.85Cro.85O4]	3,16252	8,21649	17777,03	19816,34	2039,313
6	Mg[Fe0,4 А10.8Сго.804]	3,16594	8,22537	17792,00	19799,39	2007,38
7	Mg[Feo,5 Alo.75Cro.75O4]	3,16939	8,23432	17806,97	19782,33	1975,35
8	Mg[Fe06 Alo.7Cro.7O4]	3,17286	8,24335	17821,95	19765,17	1943,22
9	Mg[Fe0,7 A1q 65Cro.6s04]	3,17636	8,25244	17836,92	19747,92	1910,99
10	Mg[Fe0.8 А10.бСго.б04]	3,17989	8,26161	17851,89	19730,57	1878,67
11	Mg[Feo,9 Alo.55Cro.55O4]	3,18344	8,27084	17866,86	19713,13	1846,26
12	Mg[Fe10 Alo.5Cro.5O4]	3,18702	8,28014	17881,84	19695,60	1813,76
13	Mg[Fei.2 А1о.4Сго404]	3,19426	8,29895	17911,78	19660,29	1748,50
14	Mg[Fei.5 Alo.25Cro.25O4]	3,20530	8,32763	17956,77	19606,73	1650,02
15	Mg[FeL8 Alo.Ao.A]	3,21656	8,35687	18001,62	19552,51	1550,88
16	Mg[Fe20 Alo Cr0O4]	3,22417	8,37666	18031,57	19516,03	1484,45
Система магноферрихромит - магноферрихромпикатит - магнопикатит (линия А - А13+)
17	Mg[FeL0 Al0Cr10O4]	3,21274	8,34697	17962,63	19570,83	1608,19
18	Mg[Fe0.95 Alfl.10Cr0.95O4]	3,20695	8,33190	17943,03	19598,78	1655,75
19	Mg[Fe0 9AI о.2Сго.904]	3,20120	8,31698	17923,42	19626,57	1703,14
20	MgfFeo.ssAl 0.3СГ0.85О4]		8,30221	17903,82	19654,17	1750,35
21	Mg[Feo,gAl 0.4СГ0.8О4]	3,18989	8,28760	17884,21	19681,58	1797,37
22	Mg[Fe0 75AI fl.5Cro.75O4]	3,18433	8,27314	17864,60	19708,80	1844,19
23	Mg[F eg,? Al о.бСго,704]	3,17883	8,25884	17845,00	19735,80	1890,80
24	Mg[Feo.65Al fl.7Cro.65O4]	3,17339	8,24471	17825,39	19762,58	1937,18
25	Mg[Fe0.6Alo.8Cro.604]	3,16801	8,23075	17805,79	19789,13	1983,34
26	Mg[Feo.55Al fl.9Cro.55O4]	3,16271	8,21696	17786,18	19815,44	2029,25
27	Mg[Fe0,5Al i,oCr0,504]	3,15747	8,20336	17766,57	19841,49	2074,91
28	Mg[Feo4Al 1.2Сго,404]	3,14721	8,17670	17727,36	19892,78	2165,41
29	Mg[Fe0.3Al 1.4Сго.з04]	3,13725	8,15082	17688,15	19942,88	2254,73
30	Mg[Feo.2Al 1,бСг0 2O4]	3,12760	8,12576	17648,94	19991,70	2342,76
31	Mg[Feo,iAl 1.8оСгод04]	3,11830	8,10159	17609,73	20039,10	2429,36
32	Mg[Fe0Al 2,оСго04]	3,10935	8,07834	17570,52	20084,93	2514,41
Система магнохромит - магноферрихромпикатит - магноферрипикатит (линия Crj+ - С)
33	Mg[Feo,o Alo.oCr2,o04]	3,20153	8,31782	17893,70	19625,01	1731,31
34	Mg[Fe0 05 Al0.05Cr1.9O4]	3,19950	8,31257	17889,07	19634,81	1745,74
35	Mg[Fe01 А1одСг18O4]	3,19749	8,30733	17884,43	19644,59	1760,15
36	Mg[Feo2 Alfl,2Cri 6O4]	3,19348	8,29692	17875,17	19664,08	1788,91
37	Mg[Fe0.3 Alo.3Cr1.4O4]	3,18951	8,28659	17865,90	19683,47	1817,56
38	Mg[Fe04 А1о.4СГ1.204]	3,18556	8,27634	17856,64	19702,76	1846,12
39	Mg[Feo.5 Alo 5Cri.o04]	3,18165	8,26617	17847,37	19721,94	1874,57
40	Mg[Fe0.6 А1о.бСго.804]	3,17776	8,25608	17838,10	19741,02	1902,91
41	Mg[Feoj Alo.7Cro.6O4]	3,17391	8,24608	17828,84	19759,99	1931,14
42	Mg[Fe0 8 А10 8СГ0.4О4]	3,17009	8,23616	17819,57	19778,84	1959,26
43	Mg[Feo,9 Alo.9Cro.2O4]	3,16631	8,22632	17810,31	19797,57	1987,26
44	Mg[Fe! 0 Ali оСго,о04]	3,16256	8,21658	17801,04	19816,17	2015,13

описываются линейными уравнениями с высокой точностью (рис. 2). Это означает, что в трехмерном пространстве «состав (Fe/’Al/'Cr? J2 - свойство» изменение свойств (межцентренное расстояние фрагментов, параметр решетки, энтальпия взаимодействия, энтальпия решетки, энтальпия образования кристаллической шпинели) можно также с высокой степенью достоверности описать уравнениями плоскости. Для нахождения уравнения соответствующей плоскости достаточно знать значения свойства в вершинах треугольника составов, что не представляет труда определить по

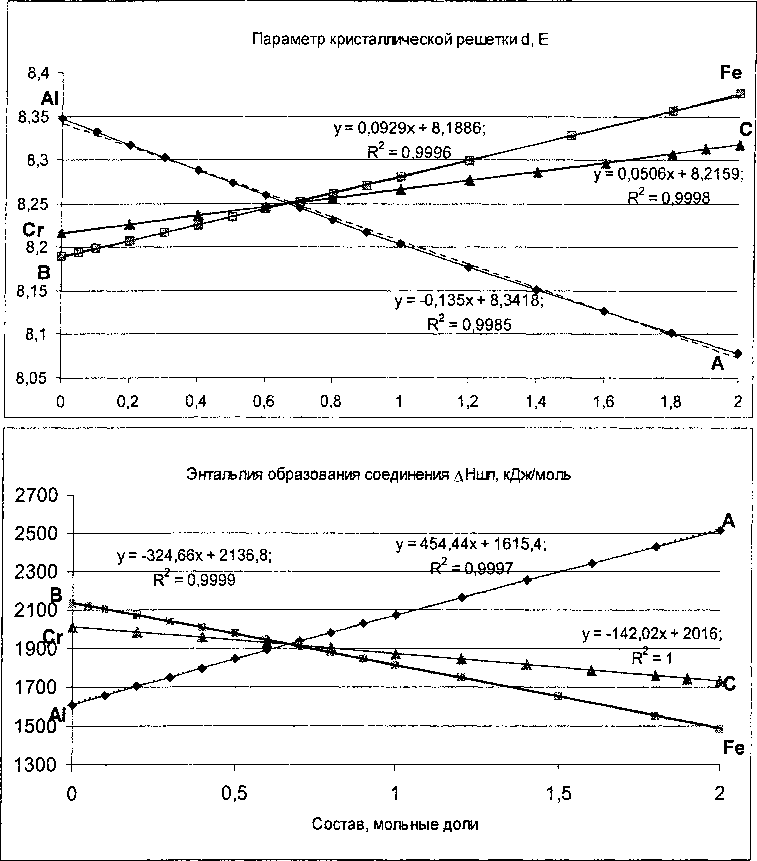
Рис. 2. Изменение параметра кристаллической решетки и энтальпии образования кристаллической шпинели Nlg2+KFex3*Aly3*Cr/+)2O4] при изменении состава по линиям Fe3+- В, А13+- А и Сr3t- С треугольника составов (рис. 1)

изложенной выше методике. Определив свойства в этих точках, из уравнения плоскости можно определить проекцию одинаковых значений свойства (параметра решетки или энтальпии) на треугольник составов.

На рис. 3 приведены проекции сечений плоскости свойств (параметра решетки и энтальпии образования) плоскостями сечений с одинаковым значением этих свойств на треугольник составов. С использованием приведенных на рис. 3 данных можно определить эти свойства хромишпинелей состава Mg[FexAl jCr^OJ при любом соотношении трехзарядных катионов.

Аналогичные расчеты параметров структуры и энтальпии образования шпинели состава (Mg23Te/+)[(Fex3+Aly3+Crz3+)2O4] при других значениях z и j показали, что замена во внешней сфере катиона Mg2+ катионом Fe2+ ведет к изменению свойств соединения также по линейному закону. На рис. 4 приведены проекции сечений плоскости свойств шпинели на треугольник составов при z = 0 и у = 1. Из сравнения данных, представленных на рис. 3 и 4 следует, что характер изменения свойств магношпинелей Mg[Fe2AlyCrz04] и феррошпинелей Fe[Fe2AlvCr,04] аналогичен, однако линии проекций одинаковых значений свойств при z = 1 и у = 0 на треугольник составов (FeI3+Al/+Cr23+)2 не параллельны. Это означает, что свойства (параметр решетки, энтальпию решетки, энтальпию образования соединения и др.) шпинелей (Mg^Fe/^^Fe^Aly^Cr/^C^] можно отобразить в виде непараллельных плоскостей, положение и наклон каждой из которых определяется соотношением количества катионов Mg2'и Fe2+ во внешней сфере, т.е. значениями / и j. Совокупность плоскостей складывается в косую трехгранную призму, опирающуюся на треугольник составов (Fex3+Al/'Cr/')2. На рис. 5 приведена развёртка боковой поверхности таких призм, описывающих в пространстве совокупность соответствующих

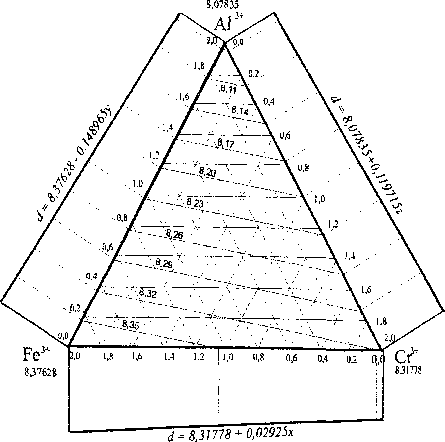
Рис. 3. Проекции уровней параметра решетки и энтальпии образования шпинели Mg[FexAlyCrzO4] на плоскость составов

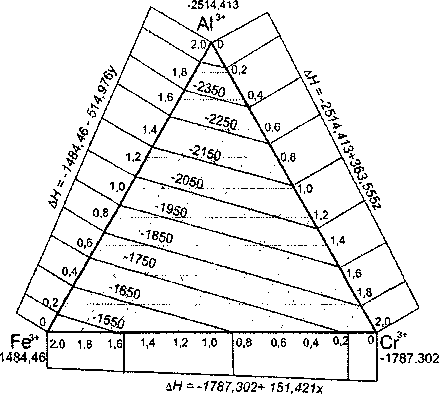
Рис. 4. Проекции уровней параметра решетки и энтальпии образования шпинели Fe[Fe,AlyCr2O4] на плоскость составов

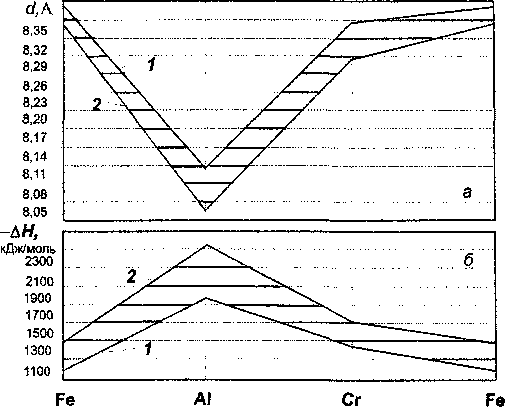
Рис. 5. Развертка боковой поверхности призм состав - параметр решетки (а) и состав - энтальпия образования кристаллической шпинели (Мд,2*Ре/*)[(Ее,3*А1у3*Сг?*)2О4] (6): 1 - при / = 0;

2 - при / = 0

параметров для всех значений переменных коэффициентов z, j, х, у и z комплексной шпинели состава (Mg^Fe/^KFe^^Al/^r/^jOJ.

Как уже отмечалось, базовые расчетные формулы 2 и 3, полученные на основе физических представлений о структуре шпинелей, в принципе не являются уравнениями первого порядка. Поэтому интерпретация свойств плоскостью вносит некоторую ошибку в построение рис. 3 и 4. Математический анализ погрешности, вызванной отклонением изменения свойств при изменении состава от линейных зависимостей, показал, что обусловленная этим ошибка при определении структурных параметров не превышает 1,8 % (относительных), а накопленная ошибка при расчете энтальпии образования кристаллической решетки не превысит 19,3 %. По нашему мнению, это позволяет с приемлемой точностью определять параметры структуры и термохимические свойства хромишпинелей даже без проведения трудоемких расчетов.

Выводы:

• 1.    Показана применимость методики расчета структурных и термохимических параметров химических соединений по разработанной ранее модели применительно к комплексным хромишпинелям.

• 2.    Рассчитаны межструктурное расстояние и параметр решетки, а также энтальпия решетки и энтальпия образования комплексных шпинелей ряда составов.

• 3.    Установлен линейный характер изменения анализируемых параметров с изменением состава.

• 4.    Построены диаграммы состав - параметр решетки и состав - энтальпия образования комплексных хромишпинелей состава (Mg²⁺Fe_/²⁺)[(Fe_x³⁺A^⁺Cr?l₂O₄].