Расчет параметров укладки теплоизолирующего материала, используемого при майнообразовании

В настоящее время большинство обводненных месторождений на Севере и в Арктической зоне России носят сезонный характер из-за ряда трудностей, возникающих при ведении гидромеханизированных работ в зимний период. Основным барьером, препятствующим ведению добычных горных работ в зимний период, служит лед. Существуют различные способы разрушения льда, имеющие свои достоинства и недостатки [1-4]. Основными недостатками известных способов разрушения льда являются высокие энергетические затраты и большая трудоемкость. Поэтому необходимы такие технические решения, которые могли бы способствовать устранению вышеперечисленных недостатков либо свести их к минимуму.

Предлагаемый способ майнообразования основан на поддержании майны с помощью покрытия поверхности водоема материалом, представленным экологически чистыми теплоизолирующими отдельностями шаровидной формы, что предотвращает льдообразование на поверхности водоемов и позволяет земснарядам и драгам свободно маневрировать [5].

При устойчивых отрицательных температурах воздуха водоем заполняют шарами, которые в результате маневрирования земснаряда или драги могут образовать два вида укладки: неустойчивую (рис. 1) или устойчивую (рис. 2).

При заполнении водоема шарами необходимо определить площадь свободной водной поверхности, а также найти зависимость количества шаров от их диаметра.

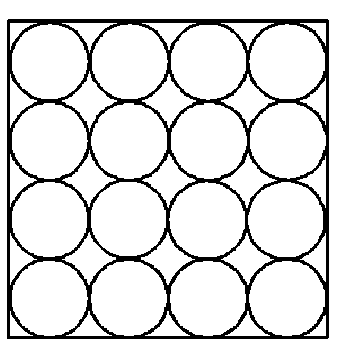
Рис. 1. Неустойчивая укладка

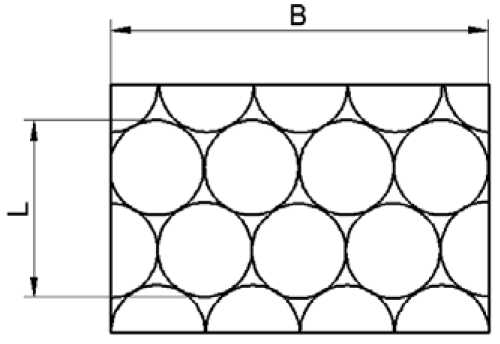
Рис. 2. Устойчивая укладка

Результаты исследования неустойчивой укладки

Площадь поперечного сечения шаров при покрытии водоема в виде неустойчивой укладки в ограниченной зоне (майне) можно рассчитать по формуле

S™ = N ' П ' Г , M , где N – количество шаров в ограниченной зоне, ед.; r – радиус шара, м.

Тогда площадь майны (условно принятой квадратной формы), покрытой шарами, составит

SKB = 4. п0 . r2, м2, где n0 – количество шаров в одном ряду, ед.

Количество шаров на 1 м2 майны определяется по формуле п=А

¹ 4 • r ²

.

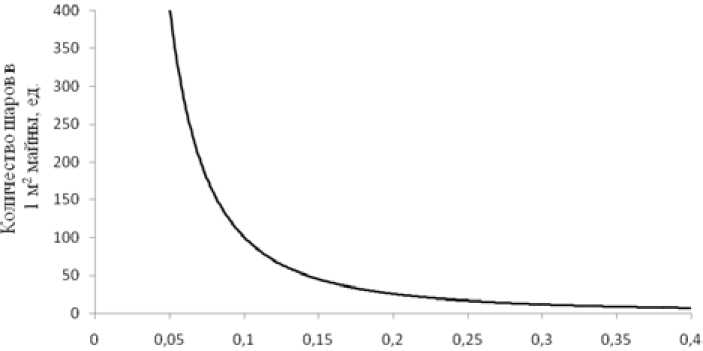
Диаметр шаров, м

Рис. 3. Зависимость количества шаров от диаметра при неустойчивой укладке

Количество шаров в 1 м2 площади майны при неустойчивой укладке обратно пропорционально квадрату их диаметра (рис. 3).

Площадь свободной водной поверхности (не занимаемой шарами) в ограниченной зоне

S n = S KB - ^Sшн = ^0,8585 • N • Г 2 , м 2 .

Таким образом, можно рассчитать площадь свободной водной поверхности на 1 м2 майны (удельная площадь пустот):

S - °'8585уг - °,2146 м2, т.е. удельная площадь пустот является постоянной величиной и составляет 21,46 %.

Результаты исследования устойчивой укладки

При заполнении водоема шарами в виде устойчивой укладки (рис. 2) площадь поперечного сечения шаров в ограниченной зоне определяется таким образом:

^{S шу -}N • ^{п r} , №.

Длина ряда шаров в укладке (рис. 2)

L - 2 • r + (n р -1) • h, м, где nр – целое число рядов, ед; h – высота равностороннего треугольника (рис. 4), вершины которого центры соседних шаров (расстояние между центрами шаров), м.

Ширина ряда в укладке

B = n в • 2r, м, где nв – количество шаров в горизонтальном ряду, ед.

При длине ряда шаров, равном 1 м, целое число рядов определяется по формуле (рис. 4)

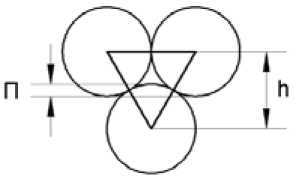
Рис. 4. Расстояние между центрами шаров и перекрытие шаров

-2 • r + h ^{n р} = h ,^ед.

Расстояние между центрами шаров рассчитывается по формуле h = tg60 • r - 1,73205 • r, м.

Величина перекрытия шаров

П = 2 • r-h, м.

Количество шаров в горизонтальном ряду на 1 м длины майны n в 2 • r ’ д.

Суммарное число рядов при устойчивой укладке

Прн = nр + hс, ед., где hс – высота сегментов, ограниченных линией АD (рис. 5), м.

Тогда площадь теплоизолирующего материала в виде шаров в ограниченной зоне опреде ляется

Sшу = nпол • П r2 + Seer , м2, где ппол - полное число шаров, ед.; Sсег_площадь сегментов, м2 (рис. 5).

Площадь сегмента:

8_С ег = П_В- S /сег

S /сег = S eek — S _A ;

, вл r - h= cos( 2 ) = r c ;

r-h

β = 2∙arccos ( _r ^c );

₁           ( r-h )

_         n- r² • 2 • arccos l - I

See- = n-r^-=,

_{S =} ^(r-hc ) • x .

SA 2;

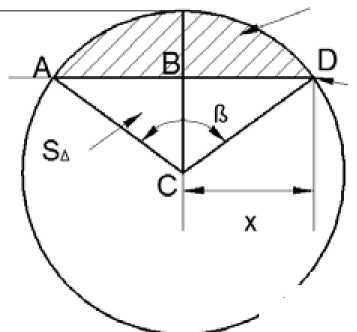
Рис. 5. Схема к определению площади сегментов, ограниченных касательной верхнего ряда шаров: hc – высота сегментов, срезанных зоной ограничения, м; S/сег – площадь одного сегмента, срезанного зоной ограничения; Sсек – площадь сектора ACD; х – расстояние BD; АD – линия, образуемая зоной ограничения майны; SΔ – площадь треугольника ACD; β – угол между радиусами AC и CD

С'

О сет

Зсск

x = tan( ^в )<г - h c );

(r-hj² • tan( ^в )

I Г — ^h= I 2 t I в n • r • 2 • arccos l-------I ( r -h ) • tanl —

c

S сег

Высота сегмента при длине зоны ограничения 1 м:

h c =1- l п + П;

l п = 2∙ n р ∙ r ;

hc = 1- nр∙2r + П, где lп – длина ряда при попадании в зону ограничения целых шаров.

В конечном итоге площадь поперечного сечения шаров в ограниченной зоне при устойчивой укладке определяется по формуле

Sшу = nпол∙π∙r + nв∙ S сег.

Для расчета площади майны, покрываемой шарами, условно выделим участок по центру двух соседних шаров через один ряд и назовем его удельным прямоугольником. Если соединить такие одинаковые прямоугольники, то получится массив устойчивой укладки шаров (рис. 6).

Площадь удельного прямоугольника

S пр = 4r²tg 60⁰ = 4 r² 3.

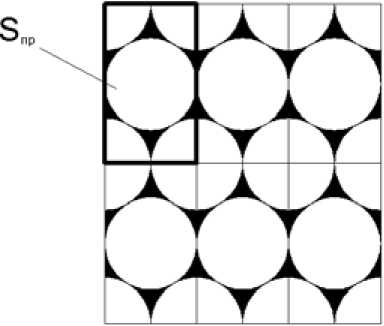
Рис. 6. Схема к определению площади удельного прямоугольника

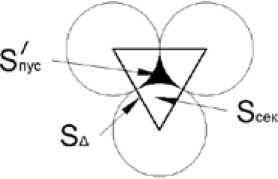
Рис. 7. Схема изображения свободной водной поверхности между шарами

Площадь свободной водной поверхности между примыкающими шарами рассчитывается

(рис. 7) так:

S/nyt = r2T3 - з•r = r21-n I y 6 I 2 J

Коэффициент пустот, показывающий отношение площади свободной водной поверхности к общей площади поверхности (площади майны):

K пус

4-S/      4•r пус

S пр

4 • r² •

= 0,093.

Таким образом, площадь свободной водной поверхности при заполнении майны шарами в виде устойчивой укладки является постоянной величиной и составляет 9,3 %.

Удельный коэффициент пустот (отношение площади свободной водной поверхности между примыкающими шарами к их площади в удельном прямоугольнике):

_K /_ш

⁴ ^ ^Snyc _;

^Sш ^/ у   ^;

4 • r

_K /_ш

2 n ^ r²

2 3 - - - I

K /ш = —---- ~ =0,103,

к где S/шу - площадь поперечного сечения шаров в удельном прямоугольнике (рис. 7).

Другими словами, на один шар в удельном прямоугольнике приходится 10,3 % свободной водной поверхности.

Заключение

В результате проведенных расчетов выявлено, что площадь свободной поверхности воды – величина постоянная, не зависит от диаметра шаров при покрытии водоема и составляет при неустойчивой укладке шаров 21,46 % от площади майны, а при устойчивой укладке шаров – 9,3 %.

Например, при покрытии водоема шарами в виде неустойчивой укладки для земснаряда 350-50Т (минимальная площадь майны 2000 м2) площадь свободной водной поверхности составляет 429,2 м2, а площадь поперечного сечения шаров - 1570,8 м2; в виде устойчивой укладки площадь свободной водной поверхности 186 м2, а площадь поперечного сечения шаров 1814 м2.