Расчет периода первого тона собственных колебаний растения злаковой культуры

При анализе технологического процесса зерноуборочных жаток часто возникает вопрос о характере взаимодействия рабочих органов жатки с убираемыми растениями. С технологической точки зрения важно, чтобы рабочие органы жатки входили в контакт с растениями без удара. В частности, одним из критериев выбора режима работы мотовила (рис. 1) является отсутствие потерь свободным зерном, которое является результатом удара планки мотовила по растениям. Для исключения нежелательных технологических явлений в работе мотовила на практике выбирают такую траекторию его движения (рис. 2), при которой величина абсолютных скоростей точек планки не превышает допустимых значений [1], а векторы скорости направлены вдоль стеблей (вертикально вниз) в момент входа планки в стеблестой. Движение любой точки планки мотовила может быть задано системой двух алгебраических уравнений

классифицируется как ударное взаимодействие. Схожее определение удара можно найти в учебной литературе, когда под явлением удара понимают изменение скорости тела на конечную величину за короткий промежуток времени. При этом четкого указания о том, что считать «коротким промежутком времени» обычно не приводится.

Рис. 1. Внешний вид мотовила зерноуборочной жатки

У(t)= Ve ■ t +

R • cos - arcsin I

V e

R • ror

+ CL • t

J

<

z (t ) = l + V- — ror

-

R • 1

-

V e

2 ;

R • ror

(

R • sin - arcsin

I

V e

R • ror

+ ror • t

J

где yOz – декартова система координат, начало которой совмещено с основанием растения; V e – переносная скорость мотовила; R – радиус мотовила; ω y – относительная угловая скорость мотовила; l – высота растения; t – время.

Величина и направление абсолютной скорости планки мотовила является главным критерием, на основе которого в механике сельскохозяйственных машин контакт планки с растением

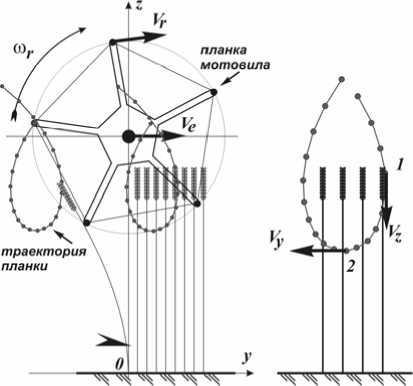
Рис. 2. Траектория движения планки мотовила и схема взаимодействия с растениями:

1 – точка начала контакта планки и растений; 2 – точка завершения контакта

Гутров Михаил Александрович, кандидат технических наук, доцент кафедры «Сопротивление материалов».

С позиций механики деформируемого твердого тела ударное взаимодействие обладает двумя признаками: кратковременность процесса и возникновение весьма больших ударных сил. Последний признак, по всей видимости, является следствием быстротечности процесса удара и возникающих при этом значительных ускорений в соударяющихся телах. Кратковременность действия значительных по величине сил инерции приводит к возникновению в телах различных волновых процессов. Кильчевский Н.А. в монографиях, посвященных теории соударения твердых тел [2], определяет термин «удар» как быстропротекающий механический процесс. Под продолжительностью быстропротекающего процесса понимается такой интервал времени, который значительно меньше периода собственных колебаний одного или нескольких взаимодействующих тел. Таким образом, величина периода первого тона колебаний разделяет ударное и неударное взаимодействие и служит основным критерием возникновения ударных явлений при контакте двух и более тел.

Применительно к механике взаимодействия планки мотовила и убираемых растений можно утверждать, что их контакт сопровождается ударом, если период собственных колебаний отдельного растения либо планки мотовила будет значительно больше времени удара. Следовательно, чтобы выбрать безударный режим работы мотовила необходимо знать 3 параметра: продолжительность времени контактного взаимодействия планки с растением, а также периоды низших круговых колебаний планки и отдельного растения. Период собственных колебаний планки или растения можно найти путем решения задачи о свободных колебаниях соответствующего тела. Из 2 рассматриваемых тел (планка и растение) необходимо выбрать то, которое имеет наибольший период собственных колебаний на первой частоте. Из теории колебаний следует, что более жесткому телу соответствует более высокие частоты собственных колебаний и, соответственно, меньшие значения периодов колебаний. Говоря о поперечных колебаниях тел, следует отметить, что конструкционная из-гибная жесткость поперечного сечения мотовила, а также жесткость его отдельных планок, безусловно, намного больше жесткости поперечного стебля на изгиб. Следовательно, для оценки технологического процесса контактного взаимодействия планки с растением на предмет возникновения ударных явлений необходимо в первую очередь сравнивать период собственных колебаний растения на первом тоне с продолжительностью времени его соударения планкой.

Для расчета собственных колебаний растения необходимо принять модель, которая бы адекватно описывала механику деформирования реального растения. В курсе лекций учебной дисциплины «Уборочные машины», которые читаются для будущих инженеров агропромышленного комплекса, а также в специальной литературе посвященной исследованию технологического процесса, растение не рассматривается как деформируемое тело. В работе [5] показано, что на основе численного решения уравнений равновесия механики геометрически нелинейно деформируемых стержней можно адекватно решить задачу контактного взаимодействия растений с планкой мотовила зерноуборочной жатки. Отдельное растение моделировалось в виде стержня c распределенными массовыми и геометрическими параметрами, жестко заделанного одним торцом. Следовательно, для определения периода и частот собственных колебаний стержня необходимо решить соответствующие уравнения динамики гибких стержней. В первом приближении рассмотрим задачу свободных колебаний консольного стержня в линейной постановке, соответствующей малым перемещениям стержня. С этой целью используем модель растения в виде жестко закрепленного одним концом стержня с равномерно распределенными параметрами, а колос имитируем сосредоточенной массой на свободном торце стержня (рис. 3). Расчет собственных частот сводится к общеизвестному решению задачи о свободных изгиб-ных колебаний стержня – расчету дифференциального уравнения четвертого порядка в частных производных д4y   m д2y

—— +---— = 0

дz ⁴ EJ _x дt ²

где EJ – жесткость поперечного сечения стебля; m – интенсивность распределенной массы стебля.

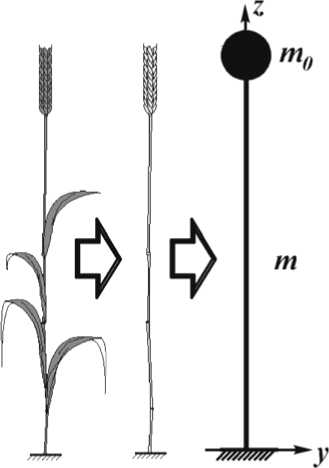
Рис. 3. Расчетная схема растения с учетом наличия колоса, m 0 – масса колоса

Для рассматриваемой расчетной схемы уравнение (1) имеет решение в замкнутой форме [3]. Полагая, что уравнение упругой линии стержня можно y (z, t) = Y (z T (t),

представить в получают систему виде двух

обыкновенных дифференциальных уравнений

T (t )" + to2 T (t )= 0Y(z)IV - a4 Y(z )= 0

где α ⁴= ω ² m / EJ x ; ω – частота собственных колебаний стержня.

Поиск решения второго уравнения системы ищем в виде суммы произведений постоянных интегрирования C i и функций Крылова K i : 4

Y ( z ) = ^ C i K i . С учетом краевых условий ин- i =1

тегрирования Y (0)=0; Y′ (0)=0; Y′′ ( l )=0; Y′′′ ( l )=- m 0 ω ² Y ( EJ )^-1 получаем систему четырех алгебраических уравнений относительно неизвестных C i

Y ( 0 ) = C 1 K 1 + С ₂ K ₂ + С 3 K 3 + C ₄ K ₄ = 0

Y ' ( 0 ) = C i K 4 + C 2 K i + С з K 2 + C 4 K з = 0

• Y "( l ) = C 1 K 3 + C 2 K 4 + C 3 K 1 + C 4 K 2 = 0

Y "(I ) = C 1 K 2 + C 2 K 3 + C 3 K 4 + C 4 K 1 = - m^L Y

I                                 a EJ

Первые два уравнения системы дают нулевые значения констант C 1 = C 2 =0. Поиск определителя системы, составленной из третьего и четвертого уравнения системы (2), приводит к частотному трансцендентному уравнению (3), расчет которого относительно неизвестного α возможен на основе графических методов, либо численных методов решения.

^^^^^^»

k

m

Или рабочим органом можно классифицировать их механическое взаимодействие. Приведенную на рис. 3 модель растения можно усовершенствовать. Введем на свободном торце стержня «толстый» стержень, который будет моделировать колос (рис. 4). Данное изменение в расчетной схеме позволяет учесть не только массу колоса, но и его геометрические параметры: l0 – длина колоса, J0=m0l20/12 – момент инерции колоса относительно оси, перпендикулярной плоскости рисунка и проходящей через центр масс колоса. Такая модель имеет больше физического сходства с реальным растением, чем модель, приведенная на рис. 3.

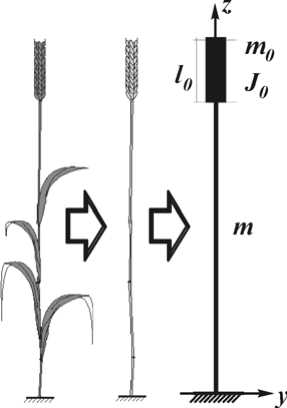
Рис. 4. Расчетная схема растения, учитывающая массовые и геометрические параметры колоса

Введенные в расчетную схему изменения требуют интегрирования уравнения (1) при других краевых условиях на свободном конце стержня. Краевые условия интегрирования уравнения (1) для расчетной схемы (рис. 4) для жесткой заделки будут равны: Y (0)=0; Y′ (0)=0. На свободном конце стержня Y "( l ) = J 0 to ² Y '( EJ )^{- 1}, Y '"( l ) = - m 0 to ² Y ( EJ )^{- 1}. С учетом того, что K 1 ( 0 ) ^ 0 ^ C₁ = C ₂ = 0 система алгебраических уравнений для расчета постоянных интегрирования C i будет иметь вид:

1         ch ( a l ) cos ( a l ) + 1

a sh (al )cos(al)- ch (al )sin (al)

где k m = m 0 / m – коэффициент, выражающий отношение массы колоса m 0 и распределенной массы стебля m .

Для установления факта наличия ударных явлений более всего нас интересует частота первого тона ω 1 , которая влияет на величину периода свободных колебаний растения T 1 . Сравнивая величину T 1 и время взаимодействия стебля с

C 3 K 1 + C 4 K 2 =

C 3 K 4 + C 4 K 1 =

J o ^ Y ‘ a¹ EJ

- m0to2 Y a3 EJ

Расчет определителя системы (4), с учетом соотношений ω ²= α ⁴ EJ / m , J 0 = m 0 l ² 0 /12, Y = C 3 K 3 + C 4 K 4 , Y ′= C 3 K 2 + C 4 K 3 , приводит к поиску корней частотного трансцендентного уравнения в виде:

K - ^K 1 + km « K 4 K

• ²   K 4 + k_m a K 3 ¹

K - K i + km O K 4 K

• ³    K 4 + km « K з  2

  = kk 2 a ² —

  m l 12

  , (5)

  
  

где k l = l 0 / l – безразмерный коэффициент, выражает отношение длины колоса к длине стебля растения.

Для поиска корней уравнения (3) и (5) необходимо знать коэффициенты kl и km, которые являются геометрическими параметрами растений злаковых колосовых культур. С учетом экспериментальных сведений [4, 5] примем отношение массы колоса и распределенной массы стебля равным km=0,861-1,205. Для середины диапазона имеем km=1,03. Соотношение средних значений длины колоса и длины стебля для 5 сортов пшеницы составляет kl=0,089-0,117 [4]. Примем в качестве исходного параметра среднее значение kl=0,10. Для указанных средних значений коэффициентов kl и km численно решим уравнения (3, 5) в системе MathCAD. Корни частотных уравнений будем искать для диапазона высот растений злаковых колосовых культур (пшеница, рожь, ячмень)0,5-1,5 м [16]. Первые 8 корней уравнения (3) для фиксированных значений высоты растений l приведены в таблице.

Таблица. Значения корней частотного уравнения (3)

l ,м	a 1	a 2	a 3	a 4	a 5	a 6	a 7	a 8
0,75	1,557	5,34	9,490	13,659	17,838	22,020	26,204	30,390
1,00	1,240	4,028	7,132	10,255	13,387	19,659	22,797	25,936
1,25	1,037	3,24	5,717	8,213	10,716	13,223	15,732	18,242

По расчетным данным, приведенным в таблице видно, что величина корней частотного уравнения α_i существенно зависит от длины стебля. Так как нас интересует только первая частота колебаний растения, то построим графики α 1 = α 1 ( l ) значений корней частотных уравнений (3, 5) (рис. 5).

®i = ai

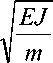
Период свободных колебаний стержня, вычис-

лим по зависимости:

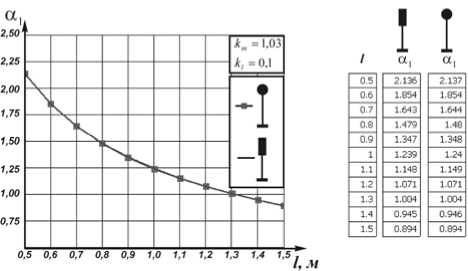
Рис. 5. Зависимость значения первого корня α 1 частотного уравнения (3, 5) от высоты растения l

t =n ®i

2n

ai

Варьирование геометрическими коэффициентами k l и k m в пределах вышеуказанного диапазона приводит к изменению значений функции α 1 = α 1 ( l ) в пределах 4%. Из графиков следует, что учет в расчете инерции поворота колоса несущественно приводит к уменьшению значения α 1 не более чем на 0,11%. Математически уравнение (5) значительно проще, чем уравнение (3). Следовательно в дальнейших расчетах можно пользоваться расчетной схемой растения, изображенной на рис. 3. По расчетным значениям корней α i уравнений (3, 5), вычислим ряд значений круговых частот стержня:

Для расчета частоты свободных колебаний необходимо знать жесткость поперечного сечения стебля. Изгибная жесткость поперечного сечения EJ реального стебля является функцией его длины l , однако изменение жесткости в пределах длины одного растения незначительно. По экспериментальным сведениям [4] межвидовое и межсортовое различие величины модуля упругости более существенно.

Примем величину изгибной жесткости поперечного сечения стебля пшеницы EJ=0,022-0,045 Нм². [5]. Для указанного диапазона жесткости по функции α 1 = α 1 ( l ) и формулам (6, 7) построим график T 1 = T 1 ( l ) (рис. 6). Приведенные графики являются предельными кривыми. Они охватывают весь существующий диапазон жесткости поперечного сечения стебля и высот растений злаковый колосовых культур. На практике для конкретного сорта и региона возделывания злаковых культур диапазон высот может быть более узким [15]. Для практического использования аппроксимируем результаты численного расчета (рис. 5) аналитической функцией в виде полинома третьей степени

n

a(l )=Z bl

■ - 0       .            (8)

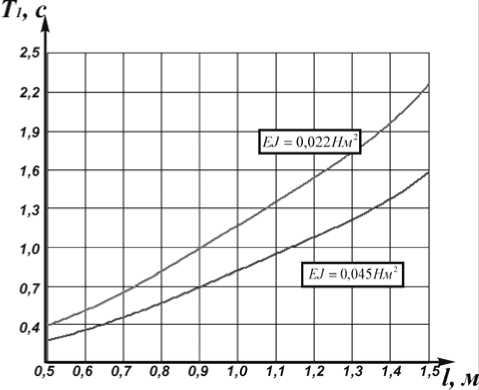
Рис. 6. Зависимость периода собственных колебаний на первой частоте от высоты растения l и жесткости EJ поперечного сечения стебля

Положим для момента времени t ₂ вертикальная составляющая скорости планки отсутствует V z = dz / dt =0. В этом случае продолжительность времени контакта, будет равна

A 1 — 1 2 — 1 1

,:.(;

— arcsin

I

-i\

J 7, (11)

где λ = Rω y / V e – безразмерный коэффициент, λ =1,1-1,8 [1] По графику (рис. 7) можно установить, что продолжительность времени контакта планки с растениями существенно зависит от рабочей скорости движения жатки и лежит в диапазоне Δ t =0,06-0,28 c.

Период собственных колебаний растения на первом тоне T 1 =0,27-2.26 c на порядок превышает диапазон времени контакта планки и растений, что позволяет утверждать об их ударном взаимодействии. Запишем равенство Δ t = T 1 . С учетом формул (10, 11) и λ = Rω y / V e имеем:

R (n

-----I-- arcsin

I V e 1 ²

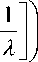
Коэффициенты bi полинома (8) для предельных значений диапазона изгибных жесткостей поперечного сечения стебля равны b= (4,39; -6,42; 4,35; -1,08) (9)

Максимальная относительная погрешность аппроксимации не превышает 1,01%. С учетом (8) период свободных колебаний (7) запишем в виде:

2n zv\ J -—0    7 \ m .(12)

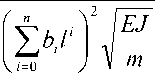
Взаимодействие рабочего органа жатки и растения будет носить ударный характер, если время контакта будет значительно меньше, чем период собственных колебаний растения на первой частоте. Следовательно, если растение злаковой колосовой культуры взаимодействует с рабочим органом менее чем T 1 =0,27-2,26 c, то такое взаимодействие можно классифицировать как удар. Однако для этого необходимо знать реальную продолжительность времени взаимодействия растения с рабочим органом жатки. В первом приближении продолжительность времени механического контакта планки с растением рассчитаем из уравнений движения точек планки мотовила. Согласно технологическим требованиям к работе мотовила, абсолютная скорость ее планки в момент времени t 1 начала контакта с растениями не должна иметь горизонтальную составляющую, т.е. V y = dy / dt =0. Время t ₂ контакта растения с планкой обусловлено моментом среза растения режущим аппаратом.

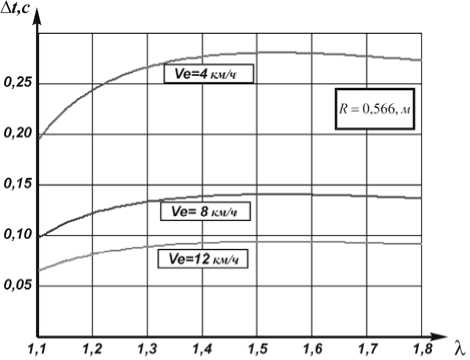
Рис. 7. Продолжительность времени контакта планки с растениями при различных значениях коэффициента λ

Из формулы (12) выразим скорость V e движения жатки по полю, получим

Ve —

R J < n2nI m ( 2

— arcsin

I

Nf

I z bl

^\ i — 0

Практическая значимость полученной функции (13) заключается в том, что она устанавливает взаимозависимость между геометрическими параметрами, физико-механическими свойствами убираемых растений и скоростью движения зерноуборочной жатки (рис. 8). Из рисунка следует, что график функции V e = V e ( λ ) содержит экстремум. Координату точки λ_э

экстремума функции (13) с учетом того, что R , m c , l , EJ , λ э не равны нулю, вычислим из уравнения:

—- = arcsin d X

X

+

^^^^^^^B

X 1

^^^^^^^B

- = 0

X

Уравнение (14) является трансцендентным. В диапазоне значений технологического коэффициента λ =1,1-1,8 уравнение имеет единственный корень λ э =1,533. На практике это значение соответствует предельной рабочей скорости V max жатки и ее максимальной производительности при условии отсутствия ударных явлений в контактном взаимодействии планок мотовила и убираемых растений.

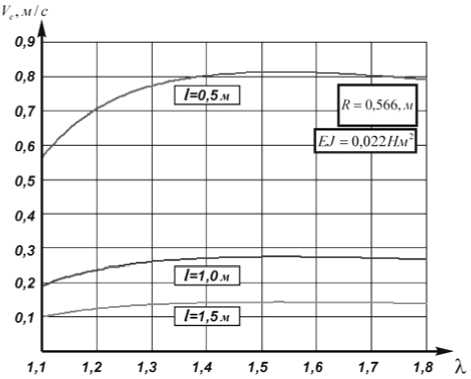
Рис. 8. Графики предельных значений рабочих скоростей зерноуборочной жатки при различных значениях коэффициента λ

Согласно приведенным графикам (рис. 8), максимальная рабочая скорость движения жатки по полю не должна превышать V max =0,3-3 км/ч. На практике технологическая скорость движения современных жаток может достигать 8-12 км/ч [1], что приводит к потерям зерна.

Выводы: полученные математические выражения (8-10, 13) позволяют классифицировать механическое взаимодействие планки и растения, а также разработать практические рекомендации к выбору рабочей скорости движения жатки с целью минимизации потерь зерна при взаимодействии растения и мотовила.