Расчет подъема воды в криволинейных капиллярах по углу наклона касательной к мениску

Введение. Поступление и продвижение почвенной влаги в растении изучается не менее 200 лет. Результаты исследований изложены в монографиях по физиологии растений — например, [1, 2]. Но интерес к продолжению изысканий в этой области не ослабевает. Так, при изучении проводимости сосудов ксилемы экспериментально установлено, что диаметр и проводимость сосудов первичной и вторичной ксилем связаны с количеством почвенной влаги [3, 4]. В [5] рассматривается роль древесных структур как хранилищ воды. Данный вопрос напрямую связан с ее подъемом и распределением в ксилеме. В работах [6, 7] нами исследованы модели продвижения воды в ветвящихся многоуровневых

Процессы и машины агроинженерных систем

прямолинейных капиллярных системах. Показано, что распределение воды в наклонных ветвях подчиняется общему правилу: в ветвях самого нижнего уровня вода продвигается дальше, чем в ветвях уровней, расположенных выше. При этом вода в вертикальном капилляре поднимется тем выше, чем больше боковых ветвей в капиллярной системе. Авторами [7] рассмотрены модели продвижения воды в капиллярных системах древесных стволов с учетом возможности ее горизонтального перемещения в сосудах ксилемы. Получено соотношение площадей капилляров по высоте ствола, обеспечивающее подъем воды в сосудах ксилемы. Выявлены соотношения для определения продвижения воды в криволинейных капиллярах, описываемых различными математическими функциями. В частности, рассмотрены ветви, вид которых описывается степенными и показательными функциями. Распределение воды в таких криволинейных ветвях и вертикальном капилляре аналогично полученному в [6]. Отличие состоит в том, что при прочих равных условиях объем воды в криволинейных капиллярах всегда больше, чем в прямолинейных. Авторы [8] с помощью фазово-контрастной рентгеновской томографии изучили механизм движения воды в сосудах растения и положение водного мениска в эмболированных газом сосудах.

Однако до настоящего времени не описана методика, позволяющая рассчитывать распределение воды в многоуровневых капиллярных системах с криволинейными капиллярами (каковыми являются реальные растения [9]) и определять положение в них водного мениска.

Цели работы:

• —    моделирование распределения воды в многоуровневых симметричных капиллярных системах с криволинейными капиллярами;

• —    расчет подъема воды в криволинейных капиллярах по углу наклона к горизонтали касательной к мениску воды в капилляре;

— определение координат менисков воды в капиллярах различных уровней.

Основная часть. Рассмотрим продвижение воды в капиллярной системе, имеющей криволинейные ветви второго яруса (рис. 1), которые, как и ветви первого уровня, описываются уравнением f ( x ) = h = k xn .

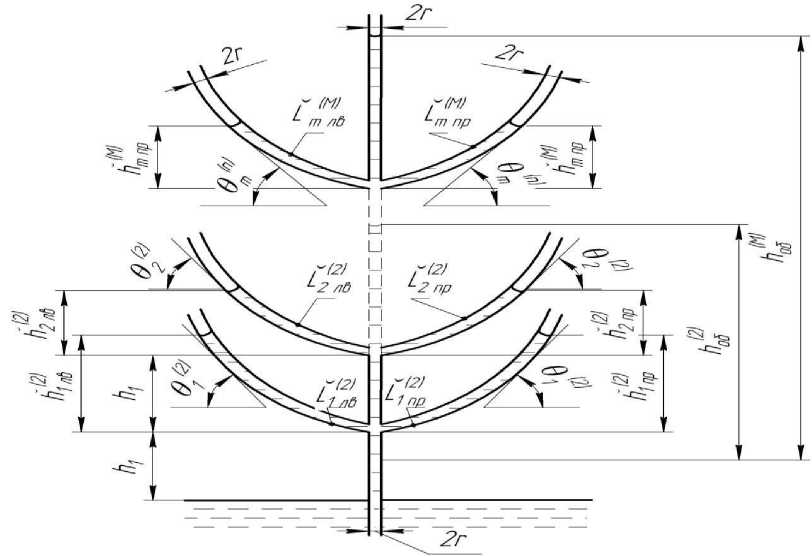
Рис. 1. Многоуровневый криволинейный капилляр

Для простоты положим, что радиусы всех капилляров равны r , расстояние между ветвями первого и второго яруса равно h 1 .

Примем следующие обозначения для величин L , h и 9:

• —    верхний индекс показывает общее количество уровней боковых ветвей в рассматриваемой модели;

• — нижний индекс показывает номер уровня, к которому относится рассматриваемая величина;

— дуга над L , h показывает, что рассматриваемая величина относится к криволинейной капиллярной системе.

В нижней части вертикального капилляра между поверхностью воды и боковыми криволинейными ветвями первого уровня (высота h 1 ) на воду действуют пять одинаковых сил поверхностного натяжения в менисках двухуровневой системы.

Силы поверхностного натяжения в криволинейных капиллярах второго уровня одновременно воздействуют: — на часть воды вертикального капилляра (пропорционально одной пятой высоты h 1 );

— на отрезок вертикальной части капилляра высотой h 1 между первым и вторым уровнями (пропорционально одной трети h 1 ).

Таким образом, уравнение y (x) = h 1 + k xn для ветвей второго уровня может быть записано в виде f (x) - h = ^h 1 + |h 1 + k xn, откудаf *(x) = tg 9, и, учитывая, что x = ^~^J~~^~, получим

9 (2) = arctg [ к n ^{( J} (^^¹ ) n ^-1].

Приведенные соотношения позволяют сделать следующий вывод. В криволинейных капиллярах в ветвях второго уровня вода продвигается так же, как если бы в системе был только один уровень — то есть два криволинейных капилляра, симметрично расположенных в одном уровне относительно вертикального. Это верно при условии, что сила поверхностного натяжения в этом капилляре поднимает объем воды, пропорциональный не высоте h 1 , а высоте (| + ^О ^ь что приводит к изменению угла наклона касательной к мениску.

Используя эти рассуждения, можно записать уравнения для продвижения воды в каждой из капиллярных вет- вей двухуровневой системы.

Для ветвей первого уровня:

9(2) = arctg[kn ( J^-р1-)n-1 ],

| nr2pg h 1 + nr2pg l!^ (x) = 2 nrо cos a,(2)

| nr2pg h 1 + nr2pg L™^x) = 2 nrо cos a.(3)

Для ветвей второго уровня:

922) = arctg [k n (J^-^P^1)n-1 ],(4)

| nr2pg h 1 +1 nr2pg h 1 + nr2pg I^/x) = 2 nrо cos a,(5)

| nr2pg h 1 +1 nr2pg h 1 + nr2pg Z^),,)(x) = 2 nrо cos a.(6)

Для вертикального капилляра:

nr2pg ( H^g - 2h 1) +1 nr2pg h 1 + | nr2pg h 1 = 2 nrо cos a.(7)

Процессы и машины агроинженерных систем

Приведем решения уравнений (2), (3), (5)-(7) относительно величин продвижения воды в капиллярах и в вертикальной ветви.

Для ветвей первого уровня:

Для ветвей второго уровня:

^йр) = ^22()лв) = (h - (| - |) h 1)/(1 - cos arctg[kn("р^р^1)n - 1]).(9)

Для вертикальной ветви:

Н(0б = h + (2 -1 - |) h 1.(10)

Из соотношений (8)-(10) видно, что наличие капилляров второго уровня обусловливает увеличение высоты подъема воды в вертикальной части и увеличение продвижения воды в капиллярах первого уровня. Действительно, определяя из (8) и (9) высоты подъема воды и составляя их разность, получим

»(;Пр)(,в)- «((Пр)(лв)=(h - (h 1) - (h - ci+;) h 1)=। h 1,                                 си), т. е. увеличивается высота подъема воды в нижнем капилляре, а следовательно, и значения ее продвижения Х(1) ^ и

( )

^1(лв) в ветвях нижнего уровня. Об этом также свидетельствует изменение угла наклона касательных к мениску воды в капиллярах первого и второго уровней.

Следуя представленной выше логике рассуждений и вводя соответствующие обозначения для ветвей, например, 5-го уровня, предположим, что расстояние между всеми уровнями равно h 1 . Таким образом получим следующие соотношения:

9(5) - arctg [k n Сj^^)n - 1],(12)

9(5) - arctg[kn(^)n - 1],(13)

9(5 ) -arctg[kn (pEEpEE)n - 1],(14)

9(5 ) -arctg [ kn (pEEEEEE) n - 1],(15)

9(5 )-arctg[kn ("pEEEEEEEE)n - 1].(16)

Если в системе M уровней, то

9(M) - arctg [k n (pEpEE)n - 1],(1

где M — количество уровней в капиллярной системе; m — номер рассматриваемого уровня.

Отсчет уровней в (17) следует вести сверху вниз.

Соотношения для величины продвижения воды в криволинейных капиллярах и высоты ее подъема в вертикальной ветви для пятиуровневой системы принимают следующий вид:

^(ПрГ ^1^e)=( h - Е h 1)/(1 - cos arctg[ kn ( j ^ 11 ) n 1]),

4Х)= ^Lr(h - (; + 11)h 1)/(1 - cos arctg[kn(j (X fc1")11)n -1]),

C>)= C»)^h - (| + I + E h 1)/(1 - cosarctg[kn( f^' * X* "^ )n ’ 1]),(2°)

C>)=ЗSlв)=С h-( 14 4+ n) h 1)/(1 -cosarctg [ knCjEEEEIE) n - 1]),(21)

iiV2?^)-(h-(| + Ы + Ь E) h 1)/(1 - cosarctg [ kn (j1"(^ ^ ^ ^11)11) n ~ 1]),(22)

C= h + (5 - 54-7-1-4 h 1.(23)

Общие выражения для криволинейной капиллярной системы из M уровней могут быть записаны в виде:

∑

Щр/лв) = (h - h 1 E?M) 2;4)/(1 - cos arctg [kn(j(E”)n- 1]),(

^жоб - h + (M) h 1 - h 1£Гм)4еГ(25)

Сравнивая величины продвижения воды в вертикальном капилляре и в криволинейных капиллярах разных уровней, полученные в уравнениях (11)-(25), можно отметить следующее:

— в криволинейных капиллярах по мере увеличения количества уровней величина продвижения воды в каждом более высоком уровне меньше, чем в капиллярах предыдущих уровней;

— наибольший угол наклона касательной к мениску имеет место в капилляре самого нижнего уровня, и этот угол уменьшается в каждом последующем уровне;

— высота подъема воды в вертикальном капилляре увеличивается по мере роста «этажности» капиллярной системы.

Для полного описания продвижения воды в криволинейных ветвях разных уровней необходимо определить координаты менисков воды в этих уровнях относительно осей у и x , связанных, соответственно, с осью вертикального капилляра и поверхностью воды. Для решения этой задачи необходимо найти уравнение касательной к мениску для функции, заданной выражением

у ( x ) = h i + k xn .

Уравнение касательной к графику функции в общем виде [10]:

У = f ( Хо ) + f '( xo )( x - xo )-

Определим абсциссу x ₀ в точке касания касательной мениска, считая угол наклона касательной 9 к прямой у = 0 заданным.

Очевидно, что

откуда

Тогда

f ’ ( x 0 ) = tg 9 = k n x 0 ( n 1),	(27)
(      ) x 0 =  J^	(28)
f ( x 0 ) = h 1 + k ("""Jg ) '7 ,	(29)
f * x 0 ) = k n (""^ )' ■ - 11	(30)

С учетом М уровней (1< m <  M ) капиллярной системы (см. (24) и (25)) уравнение касательной (26) может быть записано в виде

' tg в^(-) ) ( n - 1) ( x    ⁷¹"У I tg eW ) =

x kn ( ^У^Щ (n - 1) x.

v \ kn 7

у = m h 1 + k(  ^J^P))n + kn ( m h1 +(1 - n) k((  ^^l-)) n +

Полагая у = 0, получим значение x в точке пересечения касательной оси абсцисс: xу = 0 = -( m h 1 + (1- n ) к ( (”" "^^I P ) n )/( kn ( (”" "^Я! ^- )⁽ n ^- ^

Вычитая из (28) (32) и умножая на tg 9 ^(m) , получим значение величины ординаты у ₀ водяного мениска в m -й ветви:

у 0 = ( x 0 - x । у =0 ) tg 9™ = [ ("" jl^- + ( m h 1 + (1- n ) k Г J^nⁿ )/ /( kn (^"Я^ n ^-1))] tg 9 ^(m) -

Воспользовавшись выражением (17), можно получить соотношения для определения координат водного ниска:

ме-

(      )

[   (√ x0 = J-------

∑(  )

)ⁿ⁻¹

,

(      )

[    (√        ^{∑ (  )}        )ⁿ⁻¹ ]

у 0 = ^[     I--------------------------^{+ (} m h 1 ^{+ (1 - n} ) ^{k (}

(      )

[    (√        ^{∑ (  )}        )ⁿ⁻¹ ]

J--------------------) n ) /

(      )

[   (√ ^{—   ∑ ( )}       )ⁿ⁻¹ ]

/( kn (   J--------------------

') ⁽ n ^{- 1)})] X tg [ kn ( [

∑ ( )

к

■) n ^-1].

Аналогично могут быть получены соотношения продвижения воды и координаты водных менисков в капиллярах, описываемых другими математическими функциями.

В таблице 1 представлены углы наклона касательной к мениску в градусах, определенные как величина арктангенсов для двух-, трех-, четырех- и пятиуровневых систем, вычисленные с точностью до 10’.

Процессы и машины агроинженерных систем

Таблица 1

Углы наклона касательной к менискам при изменении М от 2 до 5

№ уровня	k 1
	0,2	0,4	0,5	0,6	0,8
Двухуровневая система
1	630	62030’	62017’	61054’	61024’
2	6206’	60030’	59036’	58030’	56018’
Трехуровневая система
1	6306’	62048’	62036’	62024’	620
2	62030’	61042’	61020’	60042’	59036’
3	61042’	59042’	58024’	570	53036’
Четырехуровневая система
1	63012’	62054’	62048’	62036’	62018’
2	62048’	62з12’	61048’	61030’	60042’
3	62018’	6106’	60024’	59036’	57054’
4	61024’	58048’	57018’	55024’	50030’
Пятиуровневая система
1	63012’	630	62054’	62048’	62036’
2	62054’	62024’	62012’	61054’	61024’
3	62036’	61042’	61012’	60042’	59036’
4	6206’	60030’	59036’	58042’	56024’
5	61012’	58012’	56018’	540	47024’

Анализ данных таблицы позволяет сделать вывод, что при k 1 = 0,2 разница в величине углов для первого и второго уровней составляет 1 и 2 0 , а при k 1 = 0,6 – 3 0 и 8 0 — соответственно, для двух- и пятиуровневой систем. Кроме того, в двухуровневой системе при изменении k 1 от 0,2 до 0,8 величина угла изменяется для ветвей первого нижнего уровня на 2 0 , а для ветвей второго уровня на 6 0 . Для пятиуровневой системы при изменении k 1 в тех же пределах величина угла изменяется на 1 0 для первого уровня и на 14 0 — для пятого.

Выводы.

• 1.    В капиллярных системах с криволинейными боковыми ветвями величина продвижения воды характеризуется углом наклона касательной к водному мениску в капиллярной ветви.

• 2.    По мере увеличения количества уровней угол наклона касательной к менискам в криволинейных ветвях уменьшается по сравнению с первой криволинейной ветвью. Уменьшение этого угла показывает, что вода в криволинейных ветвях продвигается тем меньше, чем больше номер уровня.