Расчет погрешностей определения координат точек тепловизионных изображений, получаемых при дистанционном обследовании технического состояния воздушных линий электропередачи

В России общая протяженность магистральных воздушных линий (ВЛ) электропередачи составляет более 120 тыс. км [1]. На протяжении всего срока службы ВЛ подвергаются негативным воздействиям окружающей среды, приводящим к их износу и появлению риска повреждений. Поэтому в процессе эксплуатации ВЛ требуется диагностировать и своевременно устранять возникающие в них повреждения, что сопряжено с необходимостью точного определения координат мест таких повреждений.

В настоящее время диагностика состояния ВЛ осуществляется традиционной системой профилактического обслуживания, основанной на очередных и внеочередных обходах и визуальных осмотрах. Облеты на вертолетах типа Ми-2 или Ми-8 в значительной мере облегчают осмотр труднодоступных участков ВЛ, но они проводятся вручную, требуют значительных затрат, а также наличия авиационной инфраструктуры. Как правило, облеты ВЛ проводит бригада обслуживающего персонала. Каждый член бригады проводит осмотр «своих» элементов ВЛ при помощи бинокля с высоты бреющего полета (100-150 м от поверхности земли) и старается успевать заполнять дефектную ведомость. Выполнить это весьма непросто, поскольку крейсерская скорость полета вертолета составляет 100—120 км/ч.

Таким образом, недостатками традиционной системы профилактического обслуживания являются низкая оперативность, низкая точность координат мест выявленных аварийных и предаварийных состояний энергетических объектов, большая трудоемкость, повышенная опасность проведения работ.

Выполнять задачу диагностики состояния и определения места повреждения линий электропередач и других объектов электроэнергетики способны средства тепловизионного обследования [2] (рис. 1), позволяющие без вывода оборудования из работы выявлять дефекты на ранней стадии их развития и проводить соответствующие предупредительные ремонты. Это минимизирует возможность преждевременного выхода оборудования из строя, а также снижает вероятность аварийных отказов [3].

Вследствие труднодоступности и большой протяженности линий электропередач тепловизионные наблюдения целесообразно выполнять с воздуха, т.е. наблюдения должны выполняться с борта вертолетов и других пилотируемых летательных аппаратов (ЛА). Это позволит повысить производительность диагностических работ. Однако в силу высокой стоимости аренды и эксплуатации пилотируемых ЛА стоимость таких работ весьма высока.

Снизить стоимость проведения диагностики ВЛ можно на основе использования ЛА беспилотной авиации, как правило, не требующих развертывания авиационной инфраструктуры и позволяющих повысить безопасность такого рода работ. Авторами статьи в работах

а)

Рис. 1. Снимки опоры ВЛ: а) тепловизионный; б) фотографический

б)

[4, 5] предложен комплекс диагностики ВЛ, объединяющий в себе беспилотные ЛА, аппаратуру спутниковых радионавигационных систем (СРНС) и средства получения фото- и тепловизионных изображений. Данный комплекс позволит решать задачи диагностики ВЛ в автоматическом режиме согласно сформированному полетному заданию. Далее полученные фото- и тепловизионные изображения обрабатываются с целью обеспечения их координатной привязки. Разработанный авторами алгоритм определения координат заданных точек тепловизионных и фотоизображений также приведен в источниках [4, 5].

Цель – оценка погрешностей координатной привязки изображений, получаемых при помощи диагностического комплекса, предложенного в [4, 5].

В настоящей статье решаются следующие задачи:

• •    разрабатывается алгоритм расчета значений погрешностей координатной привязки полученных фото- и тепловизионных изображений на основе аналитических соотношений, позволяющий определять погрешности координатной привязки заданных точек тепловизионных изображений без необходимости проведения затратного по времени статистического моделирования;

• •    производится расчет значений погрешностей по предложенному алгоритму;

• •    производится сравнение полученных аналитических значений погрешностей с оценками погрешностей, полученных методом статистического моделирования.

Как было указано, определение координат заданных точек аэрофотоснимков по известным значениям углов обзора камеры, координат и угловой ориентации ЛА, а также высоты его полета над поверхностью земли осуществляется в соответствии с алгоритмами, приведенными в статьях [4, 5]. Блок-схема алгоритма определения координат центра и углов снимков приведена на рис. 2.

В результате использования данного алгоритма потребитель получает значения абсолютных координат заданных точек снимков в системе широта, долгота, высота, что позволяет в дальнейшем наносить обнаруженные точки повреждений на карту без каких-либо дополнительных вычислений.

Как и для режима определения координат, для реализации расчета погрешностей требуется знание исходных значений координат и угловой ориентации беспилотного ЛА, на борту которого установлена камера тепловизора: широту – lat ; долготу – lon ; высоту – h ; азимут – az ; угол места – um ; крен – kr , а также углы обзора камеры тепловизора – ax ; ay и высоту полета ЛА над землей – dh , определяемую при помощи барометрического или радиовысотомера.

Кроме исходных данных, требуемых для решения задачи определения координат, необходимо значение погрешностей измерения этих исходных данных, в частности:

• –    σ _dh – среднеквадратическое отклонение (СКО) погрешности определения высоты ЛА над землей при помощи высотомера;

• –    σ _lat , σ _lon – СКО погрешности определения географических координат ЛА при помощи приемника сигналов спутниковой радионавигационной системы (СРНС);

( Начало )

Ввод исходных данных lat , lon , h , dh , az , um , kr , ax , ay , i e 0 k 4

Вычисление приращений координат точек снимка в связанной с объектом системе координат

, _ fax3  , Л ay3dx = tgl у I, dy = tgl у I

Вы ks0=

НИС1 f01 0 VJ

чение на ■ ks=

правляющих к f -dx ' -dy V ^1 -dx 2 -dy 2 y

эсинусов , ks2 =

точек снимка f dx ' -dy V ^1 -dx 2 -dy 2 y

з связан . ks3=

ной с объектом f dx ' dy V -J1 -dx 2 -dy 2 y

системе ■ ks4=

координат -dx 3 dy v -^1 -dx 2 -dy 2 J

kn.=

, Вычисление направляющих косинусов точек снимка в топоцентрической системе координат    . cos( um ) - cos( az ) ' ks. +(- cos( kr )-sin( az )+sin( kr )-sin( um )-cos( az ))-ks. +(sin( kr )-sin( az )+cos( kr )-sin( um )-cos( az ))-ks. 1 x                                                   ly                                                  lz cos( um )-sin( az )-ks i. +(cos( kr )-cos( az )+sin( kr )-sin( um )-sin( az ))-ks i. +(-sin( kr )-cos( az )+cos( kr )-sin( um )-sin( az ))-ks i-x                                     у                                       z -sin( um )-ks i. +sin( kr )-cos( um )-ks i. +cos( kr )-cos( um )-ks i. V                                     x                  y                   z                          J

Вычисление расстояний от центра объектива камеры до точек центра и углов снимка dh г,- = i kn iz

Вычисление координат точек центра и углов снимка в топоцентрической системе координат ^xn i = r i" ^kn i _____________________________________________i_____________________________________________ Вычисление длин окружностей Земли

LRlat = 2п-----0-(e-)-^-, LRlon = 2п----,    ,--cos(lat)

,     ,       3                  (1 -e2 • sin2(lat)(1 - e2 • sin2(lat))2

Вычисление географических координат точек центра и углов снимка

хп. ■ 360             xni- • 360Bi = lat +--x-----, Li = lon +--z-----, Hi = h - xn •

LRlat             LRlon             iz

( Конец )

Рис. 2. Блок-схема алгоритма определения координат точек снимка

• –    σ _h – СКО погрешности определения высоты ЛА при помощи аппаратуры потребителей СРНС;

• –    σ _az , σ _um , σ _kr – среднеквадратические погрешности определения азимута, угла места и крена ЛА.

При расчете погрешностей определения координат снимком будем считать, что погрешности задания начальных значений азимута, угла места и крена ЛА являются некоррелирован-– 933 – ными между собой. В этом случае корреляционная матрица погрешностей задания априорной ориентации ЛА определяется в виде

CT^ z 0     0

P Ψ

0    ^ Um   0

0      0 Ст 22

kr

Для решения задачи расчета погрешностей необходимо выделить основные этапы в алгоритме расчета координат заданных точек тепловизионных изображений, приведенном на рис. 2.

В качестве заданных точек тепловизионных изображений принимают центр, левый нижний, левый верхний, правый верхний и правый нижний углы тепловизионного изображения [4, 5]. Данным точкам приписывают индексы i=0, 1, 2, 3 и 4 соответственно.

Согласно приведенному на рис. 2 алгоритму координатной привязки тепловизионных и оптических изображений [4, 5], получаемых с борта ЛА, на основе заданных значений направляющих косинусов на точки изображения в связанной с объектом (ЛА) системе координат осуществляется пересчет значений погрешностей параметров пространственной ориентации ЛА в погрешности направляющих косинусов пяти векторов от центра объектива камеры тепловизора до точек 0, 1, 2, 3, 4 в топоцентрической системе координат (ТЦСК). Значения направляющих косинусов в ТЦСК функционально связаны со значениями направляющих косинусов в связанной с ЛА системе координат (СК) и являются результатами косвенных измерений [6]. Прямыми измерениями являются углы пространственной ориентации ЛА.

Уравнения для расчета направляющих косинусов вектора от центра объектива камеры тепловизора до i -й точки тепловизионного изображения в ТЦСК ( kn _ix , kn _iy , kn _ix ) имеют вид [5]

kn. = cos(um) ■ cos(az) ■ ks . + (-cos(kr) ■ sin(az) + sin(kr) ■ sin(um) ■ cos( az)) ■ ks . + xxy

+ (sin( kr ) ■ sin( az ) + cos( kr ) ■ sin( um ) ■ cos( az )) ■ ks - ,

^z

kn - = cos(um) ■ sin( az) ■ ks. + (cos(kr) ■ cos( az) + sin(kr) ■ sin(um) ■ sin(az)) ■ ks. + yxy

+ (- sin(kr) ■ cos( az) + cos(kr) ■ sin(um) ■ sin(az)) ■ ks. , iz kn   =-sin(um) ■ ks- + sin(kr) ■ cos(um) ■ ks   + cos(kr) ■ cos(um) ■ ks .

iz                  ix                         iyi

При наличии погрешностей определения азимута, угла места и крена ЛА Δaz, Δum, Δkr, которые полагаются малыми по сравнению с действительными значениями азимута, угла места и крена az, um, kr, уравнения (2) запишутся в виде kn + A kn- = cos( um + A um ) ■ cos( az + A az) -Iks- + A ks - )+ ix         ixi

+ (- cos( kr + A kr ) ■ sin( az + A az ) + sin( kr + A kr ) ■ sin( um + A um ) ■ cos( az + A az )) ■ I ks i

+ (sin( kr + A kr ) ■ sin( az + A az ) + cos( kr + A kr ) ■ sin( um + A um ) ■ cos( az + A az )) ■ I ks - i_z

+ A ks -yi

+ A ks- 1 i_z

y

+

kn • + A kn •   = cos( um + A um ) ■ sin( az + A az ) ■ (ks • + A ks • ) + iy iy                                        ix ix

+ (cos( kr + A kr ) ■ cos( az + A az ) + sin( kr + A kr ) ■ sin( um + A um ) ■ sin( az + A az

ks

+ (- sin( kr + A kr ) ■ cos( az + A az ) + cos( kr + A kr ) ■ sin( um + A um ) ■ sin( az +

A ks iy

A az )) ■ ( ks i. z + A ks .

iy

+

kn . + A kn . =- sin( um + A um ) ■I ks. + A ks. 1 + sin( kr + A kr ) ■ cos( um + A um ) Jks. + A ks. 1 + iz iz                     V lx lx )                                  V ly ly )

+ cos( kr + Akr) ■ cos( um + ks + iz

Выражения (3) раскладываются в ряд Тейлора. Вследствие малости погрешностей в сравнении с действительными значениям азимута, угла места и крена в данном ряде могут быть удержаны только линейные члены разложения, компоненты разложения более высоких порядков могут быть отброшены.

Перейдя в выражении (3) к рассмотрению погрешностей измерений, получают выражение для погрешностей определения направляющих косинусов на i -ю точку изображения, которое удобно записать в матричном виде

	Fd kn. ix	d kn. ix	d kn. 1 ix
1	d az	d um	d kr
A kn. , ix A kn .y =	d kn.	d kn. iy	d kn. iy	A az • A um .                                         (4)
г	d az	d um	d kr
A kn	d kn.	d kn.	d kn.	A kr
iz J	iz	iz	iz
	d az	d um	6 kr J

Корреляционная матрица погрешностей оценки направляющих косинусов вектора i -й точки снимка в ТЦСК определяется согласно выражению

Pkn	"a kn.     a kn.     a kn. " ix      ix      ix	■ P , .	"d kn ix 5 kn ix 5 kn ix"	T "  2 ’ kn.     ’ *’,      ” k”, i,       xy       xz 2 = ’ ku;     ’,       ’ ku; i           kn ■             i xy iy 2 yz ’ *-,     ’ In     ’ ku xz       yz       iz
	8 az    d um    d kr a kn      a kn.     a kn. n iy     n iy     n iy		d az     5 um     d kr a kn.     a kn.     a kn. i y        iy       iy
	a az     d um     d kr 8 kn     8 kn     d kn iz       iz       iz		d az     3 um     3 kr a kn     a kn     a kn iz       iz       iz
	d az     d um     d kr		d az     d um     d kr

где Pkn i (3 x 3) - корреляционная матрица погрешностей определения направляющих косинусов вектора i -й точки снимка в ТЦСК. На главной диагонали матрицы Pkn i находятся дисперсии оценок направляющих косинусов векторов точек снимка в ТЦСК, а вне ее – корреляционные моменты связи погрешностей; Р.. ^— корреляционная матрица погрешностей определения уг^ловой ориентации, заданная в соответствии с (1).

Согласно приведенному на рис. 2 алгоритму расчета координат заданных точек изображений по полученным значениям направляющих косинусов в ТЦСК на основе известной высоты полета ЛА над землей определяется расстояние от центра объектива камеры тепловизора до точек тепловизионного изображения в соответствии с формулой dh

,

r = —i kn

iz где i = 0, 1, 2, 3, 4 – номера заданной точки тепловизионного изображения.

Погрешности измерения высоты полета ЛА над землей dh и определения направляющих косинусов векторов точек снимка в ТЦСК полагаются также некоррелированными, поскольку измерения угловой ориентации и высоты полета выполняются разными устройствами (аппаратура потребителей СРНС и высотомер). Исходя из этого корреляционная матрица погреш- ностей задания высоты и z-составляющей направляющих косинусов вектора i-й точки снимка в ТЦСК определяется в виде

Pdh_kni =

^CT dh

^ kniz

При наличии погрешностей измерения Δ dh , Δ kn выражение (6) принимает вид z

ri + Ar =

dh + A dh

.

kn, +A kn, i _z          i _z

Для упрощения анализа выражение (8) также раскладывается в ряд Тейлора. В силу малости погрешностей по сравнению с действительными значениями величин в рассмотрении остаются только линейные члены разложения. Погрешности измерений расстояния от i -й точки снимка до центра объектива камеры тепловизора определяются как

Д r i = * d dh

^Д dh a kn i z J [ ^Д kn i z

Далее вычисляются значения частных производных корреляционной матрицы задания высоты ЛА и z -составляющей направляющих косинусов вектора i -й точки снимка в ТЦСК Δ R _i :

Л R .	г 1	dh
Л R i	kn iz	2
		kn
	L	i z J

Вычисляется дисперсия определе н ия расстояния от i -й точки снимка до центра объектива камеры тепловизора путем на основе выражения

■2 = A R i ■ P dh_ta ■ A R i ^T . i i

На следующем этапе алгоритма расчета координат тепловизионных изображений (рис. 2) осуществляют определение координат заданной точки в 1ЦСК, что выполняется в соответствии с выражениями xn, = г ■ kn, ix      ii iy       i       iy xn, = r ■ kn, iz      ii

Можно показать, что погрешности задания значений направляющих косинусов векторов точек снимка в ТЦСК по x, у-составляющим и расстояния от камеры до i-й точки являются не- коррелированными.

При наличии погрешностей Δ kn_ix , Δ kn_iy , Δ r выражение (12) для xn _ix принимает вид

.

xn,- + A xn,- = ( r + A r ■ kn,- + A kn ix ix ^yi i X ix ix

Разложение (13) в ряд Тейлора с удержанием линейных членов дает выражения для погрешностей определения координаты xn i_x :

Axn,-ix

dxnid

---x-Ar +---x-Akn dr     i 5kn,- ii

После вычисления частных производных выражение (14) принимает вид

Axn; =kn,- "Ar + r-Akn: ix     ix i ii

Усреднением квадратов левой и правой частей выражения (15) можно определить дисперсию погрешностей определения x -составляющей координат i -й точки снимка в ТЦСК:

a2   = мГЦ- )21 = kn 2-a2 + r.2 • a2(16)

^xnx L x J     ix    r i kn

x где Ml (Лхп- )21 - означает операцию усреднения (вычисления математического ожидания) ве-Lv личины, заключенной в квадратные скобки.

Аналогичным образом можно определить дисперсию погрешности определения y-составляющей координат i-й точки снимка в ТЦСК xn iy

2    22 22

.

o _xn. = kn i - o r + r i - o y^y                   iy

Для z-составляющей координат i-й точки снимка в ТЦСК xn выражение (16) запишется iz в виде

Un, V = kn ² -A r ² + r ² -A in, ² + 2 - kn- • r -f A r -A kn, V iz) iz i i         ⁱz           iz i ( i iz

где корреляционный момент связи (Δ r_i ∙ Δ kn_iz ) оценивается ранее как (10)

R Ari-Akni^

Г

^MM ri ^ЛкПг2

Adh kn iz

dh i 2 kn iz

- Akn ² i_z

dh            2

dh 2

o kn2   kni iz       z

=-kn 2       '■ iz L

Тогда дисперсия погрешностей определения z-составляющей координат i-й точки снимка в ТЦСК xniz определяется как o2 =m|Axn l=kn,- 2-Ar-2 + r2-Akn 2-2-r-o2

.

xn            iz     iz     i i      iz      i kn iz                                                    iz

Таким образом, найдены погрешности определения координат i -й точки снимка в ТЦСК, центром которой является центр камеры тепловизора, размещенного на борту беспилотного ЛА.

Для определения погрешностей широты и долготы i -й точки требуется использование радиусов кривизны земного эллипсоида для заданных координат, в качестве которых могут выступать координаты места ЛА.

Значение радиуса кривизны сечения земного эллипсоида в меридиональной плоскости определяется параметрами эллипсоида и географической широтой места lat . При наличии погрешности определения широты ЛА Δ lat значение радиуса кривизны сечения эллипсоида в плоскости меридиана также будет определено с погрешностью Δ Rlat :

-■.    ' 0"/),   3

(1 - e ² • sin²( lat + A lat ))²

где R 0 – экваториальный радиус эллипсоида, e – эксцентриситет эллипсоида.

Выражение (21) раскладывается в ряд Тейлора. В силу малости погрешностей удерживаются только линейные члены разложения

A Rlat ■

d Rlat     .

A lat .

5 lat

При этом частная производная выражения (22) имеет значение

- 3.■ • R 0 • cos( lat )..n( lat ) . ( e ² - 1 ) ^{d a}            1 - e ■ . ,„, ■ ( lat ) ] 52

Исходя из этого определяется дисперсия погрешности определения меридианального радиуса кривизны Δ Rlat :

_а2                 -f^{S Rl} at ) 2^2

о Rlat = M [( ^{A Rlat} ) J= l у l_at I ° lat

Рассуждая аналогично (21)-(24), можно найти значение погрешности определения величины радиуса кривизны сечения эллипсоида Земли в нормальной плоскости по формуле

Далее определяется дисперсия погрешностей определения широты координат i-й точки снимка. Для этого задаются малые по сравнению с действительными значениями lat и xn ix значения погрешностей Δlat и Δ xnix

I xn i_x ^{+ A}ni_x I' ³⁶⁰

Bi + ABi = ( lat + Alat ) +^— X----- x ^j \ •

2 ^ - ( Rlat + ^ARlat )

Выражение (26) раскладывается в ряд Тейлора. В силу малости погрешностей рассматриваются только линейные члены разложения dBj         8B.-            дВ.-

АВ, = —- -A lat +--- i—A xn, +--- i— -A Rlat .                                 (27)

i дlat       dsn,      ix дRlat ix

Вычисляются частные производные выражения (27)

^{360 - xn} i..

A B. = A lat + ³⁶⁰ - A xn.--x- - A Rlat .                                (28)

i          2 n- Rlat     ix   2 n - Rlat ^{2                                          1}

Возводятся в квадрат левая и правая части выражения (27):

2 + V

2 n Rlat² I

V         7

• A Rlat +

⁺2 - A ot- An. • ——--2 - A at A Rlat ix 2 n Rlat

360xn ix

2 n Rlat

- 2 A xn A Rlat i_x

,         (29)

1802 • xni x.

n ² • Rlat

Выражение (29) усредняется. Дисперсия погрешности

определения

широты i -й точки

снимка определяется как

-B - M

= - ² +[    60 ) 2

lat V ^{2 n Rlat} )

• _— 2

xn ix

+

( 360 • xn■ xL

П- Rlat ² v

Л ²

• ^- Rlat

360 • xn i

- 2 x- • M [ A lat -ARlat ], 2 n • Rlat ²

где M[Δlat ∙ ΔRlat] – корреляционный момент связи между двумя случайными величинами, определенный как математическое ожидание произведения центрированных случайных вели- чин:

м [ A/at • ARlat]=Rt.„L                                         (31)

⁵ 'at

Таким образом, дисперсия погрешности определения широты координат i -й точки снимка определяется как

- 2 = m|

Bi ।

=- 2 +(0     - lat 12-Rlat)   xnx

( 360 • xn, ix

V 2 n Rlat ² )

• ^- Rlat

-

360 xn _i

2 x

2 n • Rlat ²

3 . e² • R 0 • cos( lat ) • srn( lat ) • ( e² - 1 ' ^ 2 ^[ 1 ^- e ²^т²⁽ l a t ) ] 52            °^la

Отметим, что четвертое слагаемое выражения (32) вносит незначительный вклад в дисперсию погрешности определения широты координат i -й точки снимка. Поэтому в дальнейших вычислениях им можно пренебречь:

^в = м i

2 Г 360 f ²

= ст ² +1I • ст ² lat V 2 n . Rlat )     xni

x

x

Л2

2n. Rlat ²

V 7

Rlat

Аналогичным образом определяются дисперсии погрешностей определения долготы и высоты i -й точки снимка.

Дисперсия погрешности определения долготы i -й точки снимка

		(360- xn.	2
„в^ My ]	2   ( 360 г 2 = ст2 +1----------1 -ст2    - lon ( 2n- Rlon )     xni	y 2 2 n - Rlon	- „R lon	(34)
	y	<           >

Дисперсия погрешности определения высоты координат i -й точки снимка

• ’V M k , > ]- -2 + «к-                        (35)

z

Таким образом, приведенный алгоритм расчета погрешностей позволяет на основе погрешностей прямых измерений рассчитывать погрешности искомых географических координат заданной точки получаемых с борта ЛА тепловизионных или фотоснимков.

Вышеописанный алгоритм расчета погрешностей аналитическим методом был использован для анализа алгоритма определения координат заданной точки изображения [4, 5], модели -рующего процесс координатной привязки получаемых тепловизионных изображений.

В частности, был произведен расчет зависимости СКО погрешности о r определения пространственных координат одной из точек тепловизионного изображения от угла азимута ЛА в соответствии с выражением

• —r - —X + —Y + —Z ,                                           (36)

где о X , о Y , о Z - СКО погрешности определения прямоугольных геоцентрических координат точки (данные координаты могут быть однозначно получены из широты, долготы и высоты на основе известных соотношений).

Кроме того, для анализа полученных результатов был произведен расчет погрешностей координатной привязки получаемых изображений методом статистического моделирования, исходя из которого на измеряемые исходные параметры накладывались погрешности в виде случайных величин с заданными значениями среднеквадратических отклонений (СКО) и нулевыми математическими ожиданиями. Затем проводилось заданное число статистических испытаний, в результате которых рассчитывались статистические оценки СКО определяемых параметров.

Расчеты производились при следующих исходных данных:

• –    координаты и угловая ориентация ЛА, определяемые аппаратурой потребителей СРНС: широта lat = 56°0' с.ш.; долгота ion = 92°0' в.д.; высота h = 400 м; азимут az = 0° - 360°; угол места um = 0°; крен kr = 0°, 10°, 20°, 30°;

• –    углы обзора камеры тепловизора типа TH7102 NEC [0]: ax = 29°; ay = 22°;

• –    высота ЛА над землей dh = 100 м, определяемая при помощи барометрического или радиовысотомера.

• —    о dh = 10 м - СКО погрешности определения высоты ЛА над землей при помощи высотомера;

• –    σ _lat = 0,032’’, σ _lon = 0,058’’ – СКО погрешности определения географических координат ЛА при помощи приемника спутниковых сигналов (указанные значения о а и о ion соответствуют СКО погрешности σ = 1 м определения координат ЛА в горизонтальной плоскости);

• -    о h = 10 м - СКО погрешности определения высоты ЛА при помощи аппаратуры потребителей СРНС;

1^ ^ r , м

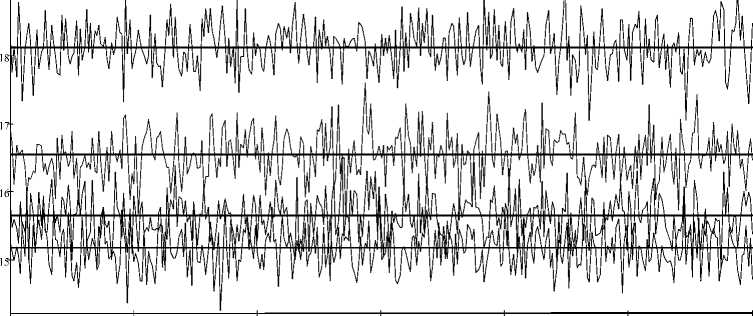
крен 30‘ крен 20° крен 10° крен 0° az,°

60                      120                     180                     240                     300                     360

Рис. 3. Зависимость среднеквадратической погрешности определения координат заданной точки от азимута ЛА

• –    σ _az = 10’, σ _um = 20’, σ _kr = 20’ – среднеквадратические погрешности определения азимута, угла места и крена ЛА;

• –    z = 1000 – число статистических испытаний в каждом заданном значении азимута ЛА.

Зависимость СКО погрешности определения координат точки левого нижнего угла тепловизионного изображения σ _r от азимута ЛА в диапазоне 0–360° при четырех значениях крена приведена на рис. 3.

Приведенные на рис. 3 зависимости наглядно демонстрируют соответствие результатов статистического и аналитического методов оценок погрешностей координатной привязки получаемых изображений. Оценки, полученные аналитическим методом, представляют собой математические ожидания оценок, полученных методом статистического моделирования.

Аналогичные результаты получены для остальных точек тепловизионного изображения.

Анализ полученных результатов расчета погрешностей координатной привязки изображений, получаемых методами статистического и аналитического моделирования, показывает, что методы имеют расхождение менее 1 %, что позволяет при необходимости оценивать погрешности только аналитическим методом по предложенному алгоритму, избегая затратных по времени вычислений, присущих методу статистического моделирования. Кроме того, дополнительным достоинством аналитического метода является возможность учета корреляции между измеряемыми значениями, для чего требуется только изменение вида корреляционных матриц измеряемых параметров (они перестают быть диагональными), при этом алгоритм расчета погрешностей не изменяется.

• [1]    URL: http://www.fsk-ees.ru/about.html .

• [2]    Сучкова Г.А. // Энергетик. 2008. № 4. С. 20–22.

• [3]    Шалыт Г.М. Определение мест повреждения в электрических сетях. М.: Энергоатомиз-дат, 1982. 312 с.

• [4]    Макаренко Г.К., Алешечкин А.М. // Современные проблемы радиоэлектроники: сб. науч. тр. Красноярск: Сиб. федер. ун-т, 2012. C. 33–37.

• [5]    Алешечкин А.М. // Вестник СибГАУ, 2011. № 7. C. 58–62.

• [6]    Винокуров В.И. Электрорадиоизмерения. М.: Высш. шк., 1986. 351 с.

• [7]    URL http://www.analyzers.ru/teplovizori/necth7102/ .

Calculation of Error in Determining the Coordinates of Points Thermal Images Obtained with Remote Technical State Survey

Overhead Power Lines