Расчет поля, формируемого геометрооптическими фокусаторами

В последнее время широкое распространение получили дифракционные оптические элементы, фокусирующие когерентное излучение в заданную область с заданным распределением интенсивности [1.2]. Появился широкий спектр работ посвященный, как вычислению светового поля, создаваемого подобными оптическими элементами, так и решению обратных задач дифракции. Однако во многих работах при решении задач дифракции используется приближение геометрической оптики. Приближение геометрической оптики справедливо в случае, если ширина зоны или размер одного пиксела (при решении задач итерационными методами) на оптическом элементе составляет несколько десятков длин волн. Это условие часто не выполняется в случае короткофокусных дифракционных оптических элементов, для расчета которых необходимо использовать более точное электромагнитное приближение. В настоящее время в электромагнитном приближении решены задачи дифракции света на простейших структурах: дифракционных решетках[1-4], шаре [4], цилиндре, круглом отверстии в металлическом экране. Это в первую очередь связано с тем, что расчет поля от более сложных пространственных структур требует больших вычислительных затрат. В связи с этим большую роль в теории дифракции играют асимптотические методы. В данной работе предлагается асимптотический метод оценки поля при дифракции на бинарной квазипериодической струк- туре, представляющей совокупность дифракционных решеток с различным периодом. Получены удобные представления для волновых полей. Дан-ный подход может быть эффективен при расчете поля от дифракционных оптических элементов.

Асимптотическая оценка поля при дифракции на одномерной бинарной квазипериодической структуре

Рассмотрим одномерную структуру, представляющую совокупность дифракционных решеток. Введем условные обозначения. Пусть Х_м границы локальных решеток, N_M -число периодов М-ной дифракционной решетки. Если N_M -> оо то квазипе-риодическая структура превращается в строго периодическую дифракционную решетку. Если N_M = 1 все периоды квазипериодической структуры имеют различный период. Обозначим х_т -границы периода локальной решетки (для границ периодов используется сплошная нумерация, независимо от того какой решетке принадлежит данный период), ^_m - ^х»м ~^хт- Не ограничивая общности подхода, рассмотрим дифракционную решетку с одним пикселом на периоде [1] (см рис.1), с_т -ширина пиксела, h - его глубина. Пусть плоская волна exp(ik(a_ox-p_oz)) падает на описанную выше квазипериодическую структуру.

Рис. 1 Вид двух зон ДОЭ, которые имеют по одному периоду разных дифракционных решеток

Рассмотрим две области:

1 - область z>0,2 - область z<0.

Поле в первой области представляет собой совокупность плоских воля

^(x.z) = ехр(/£(«_ох- Д^ + W (x,z)

-       7                         ,       (1)

W (х, z) = J Л(а) exp(/£(ax + Д1Уу1а где Д^-Jv^c? .

Нормальная производная поля

= _^д ехрО£(а_ох - Д z)) + az

+ J хкД^а^А^адехр^к^ах + pz})da ,          (2)

где /1(«) - спектр пространственных частот волн, отраженных от структуры, |а| < 1 соответствует однородным плоским волнам, |а| > 1 соответствует неоднородным плоским волнам, амплитуда которых убывает при удалении от поверхности квазипериодической структуры. Спектральная функция выражается через отраженное поле на поверхности следующим образом и •__

А(а) = — f If (x,O)exp(-ikax)dx.          (3)

2^ „

Пусть отраженное поле на поверхности структуры представляется в виде

W(x) = exp(/ta_ox)££tf^m,, exp(ik—U-xjyect(x,x_m,x_m^ m               ^Z'«

я \Hfxe[a,b] rect(x,a,b) = <

[0 else

Данное представление поля на поверхности удобно гем, что по форме совпадает с представлением отраженного поля в случае дифракции на строго периодической структуре. Нахождение поля на поверхности сводится к определению дифракционных коэффициентов R". Далее будет показано, что в асимптотике выражения для дифракционных коэффициентов в квазипериодическом случае совпадают с коэффициентами, вычисленными для строго периодической решетки с параметрами dm, ст . Этот результат является основным для асимптотической оценки поля при дифракции на квазипериодической структуре.

Суммарное поле и его нормальная производная при z<0 представляется в виде

^ ^И^^ sin! —-^Х-^-- sin^* (z +h))S^k(x) (6)

* Д          \ ^Ck v

-T- ⁼ HlL^aM ^TP ^sini —---- со$(Г/(2+Л))5*(х)

к ц             \ Ск )

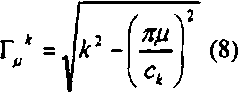
_Sk,. fb/x^x.+cj

(0            else

По аналогии с [1] запишем условия непрерывности поля и его нормальной производной на границе раздела между поверхностью дифракционной решетки и свободным полупространством.

exp(/teox)^l+ ^^Д/Ф/'М^ =

=ZEV^^'^W/*)5* w ■

^ik exp(ita_ox) - ^а₀)^^R” F" (х) J           V         пт

a.

bdk

S‘(x),

где

м ( 1кЛп, Л „ х ф =ехр-—(x-xm) re*,xm,xm+1) , I dm )

F_n^m (х)= f; (X)+ f; (x) f; (x) =д« )Ф„^т w

(И)

f^--±V№-h<^^

-Хт+х^-ех^^^

(а-а0)- — dm

-da,

«„ =«о+— •

Систему функциональных уравнений (3.10) можно привести к системе линейных уравнений M^k_P*R^kn =D^k_p,

Мкрп = iA рл "Vkdk8рп,

D р = iA ро — kdk8рй —Bp, tg(rk h\              __ xk*ck                                    I

A^kpn = ^ _k !\* p(a^k_n)D^knpD^k_Pp D^k_np = jexpOX^oX+zlfl/t^tx-xjyisin W _дГ p                             _xt                                 I

*^l\dkx ,

ск

s¹, = E^t^A«‘")a‘^‘_w .

А д1 Р t^u-ik j ^exp(^«ox)Fn(x)sin

,F„(X) = LR"F”W-

Полученная система содержит бесконечное число линейных уравнений. Для нахождения дифракционных коэффициентов необходимо оставить конечное число линейных уравнений. Пусть N = гаах(^) - максимальное число периодов, Р = тах(л) - максимальное число порядков. В этом случае размерность системы уравнений равна NxP.

Найдем коротковолновую асимптотик}'. Последнее уравнение в (15) описывает влияние различных периодов квазипериодической структуры. Ана-лизируя систему уравнений (14) отметим, что если Fn(x) = ^RnmFnm(.x)-^ti, то система (14) распа- из которых имеет размерность Р. Каждая из этих

подсистем уравнений совпадает с системой уравнений, полученной в случае решения задачи дифракции на решетке с параметрами d_m = x_m+1 - х_т, c_m,h_m. Это позволяет уменьшить вычислительную ошибку при решении системы уравнений и в дальнейшем получить удобные выражения для асимптотической оценки поля.

Для дальнейших рассуждений введем несколько вспомогательных непрерывных функций ф^ ,R_n<^ » ^a«W • Функция^(х) определяет границы зон квазипериодической решетки ^(xJ = mR , где Л-параметр квазипериодической структуры (при Л -> 0 границы зон стремятся друг к другу)

RnW=Rnm > a (xj = anm

Перепишем F„(x) в следующем виде дается на N независимых систем уравнений, каждая

Ini

Р№2№Г21 _а ..1 №)-№.”! „

а-а,

exp(ik(a-abXx-xM^)da -

Рассмотрим предельные случаи, когда влиянием соседних периодов можно пренебречь те.

^nW-*^'

[.Периодическая структура а_п^т = а„^т-' R" = ^-^т+) • ^{в этом} случае из формулы (16) следует. что F_n (х) тождественно равна нулю.

• 2 . Длина волны освещающего пучка стремится к

переменной а) от низкочастотной функции. При £(x-x_m+l)-> ос значение Фурье- образа стремиться к нулю.

• З .Л-»0Д->ос,но кХ остается конечной величиной.

нулю Л ^ О ( к —> ос), Л остается конечной. В этом случае мы имеем Фурье преобразование (по Можно показать, что

I

т+1 а-а_п

Д(а)-^аят)

expect - а_й )(х - х_{т и})) ^ О

Доказательство утверждения (17) сводится к доказательству предельной формулы

4 .^     _ _Л1 ^1 ^т ) _схр( W^) _> о при Л о.

V Л у ( Л            Л где р(хт) = Л/л , R(x) -произвольная функция.

Строгое доказательство можно провести только в случае равноотстоящих зон, однако численный анализ показывает справедливость данного утверждения для широкого класса последовательностей х_т и функций R(x)

Рассмотрим случай малых Л и получим в этом случае удобное выражение для амплитуды вблизи поверхности квазипериодической структуры. Если функция ^(х) монотонна и дифференцируема, то в пределах отрезка [хтхтт| ] справедлива линей-z s ж Л(х-х_) ная аппроксимация

M^z (х) = cxpGkaqX')'^ ^R^Mп х

xcxpf ika_ox+ik— ^(x) \dx . I A J

X exp ik—ф^х) гесЦх. х_т , х_т+1) .

V л /

Нетрудно заметить, что знак суммы можно убрать и поле на поверхности квазипериодической структуры представляется в виде.

^(х) = ехр(/А^_ох)^^_п(х)ехр|/^4^^(^) | ■ (18) п          V Л )

Поле в полупространстве имеет вид

W4x,z) = jG(x-x,zyP0(x)dx ,

I ^H₀4kFW)

G(x, z) = —-------------

2/ dz

С формальной точки зрения данный подход аналогичен методу нелинейного предыскажения, изложенного в работе [5]. Отличие состоит в том, что в этой работе дифракционные коэффициенты были найдены, исходя из геометрооптической аппроксимации поля внутри штрихов дифракционной решетки, которая справедлива, если период решетки составляет несколько десятков длин волн. В свете нового подхода дифракционные коэффициенты могут быть найдены из строгой теории дифракции. В электромагнитном приближении значения коэффициентов будут зависеть от типа поляризации и относительной ориентации векторов поляризации и направления штрихов в решетке. Существенное отличие выражения (20) от формул, полученных с помощью метода нелинейного предыскажения состоит в наличии зависимости дифракционных коэффициентов от координат.

В качестве примера рассмотрим вычисление поля от бинарной квазипериодической структуры, границы зон которой определяются формулой Ф^х_т) = тХ , где ^(х) имеет вид

<р(х) = xsinty +у(х-/sin//)' + /* cos" ц (21)

Для того, чтобы использовать (20) для нахождения поля в полупространстве необходимо определить функцию Д,(х). Для ее определения необходимо использовать значения дифракционных коэффи

циентов R" - Q_n^ldJ , которые находятся из

системы (14).

Подставляя (18) в (19) получим окончательное выражение для поля везде при z>0

W г) = £ jR_n (x)G(x - x, z) x

R„w=Qnu/dm) .та

где

Л  _______ (х -/sin/у)

^  ^(х-/sin//)² + /² cos* ц

+ sin^

График функции QW d,^ =

4-(a,-AJdJ2

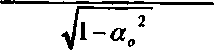
Q-i^/dJ ^.%m <1.8a₀ = sin

для ТМ-поляризапии приведен в работе [6].Из результатов, приведенных в работе, также видно, что Q_n =0 если п * -1,0 . Функцию Q_o можно найти из закона сохранения энергии Q_² -vQ² = 1.

Результаты вычисления поля приведены на рис. 2. Анализируя полученные результаты можно заметить, что при коротких фокусных расстояниях (т.е. сравнимых с размером оптического элемента) наблюдается асимметрия формы фокального пятна и смещение относительно точки предполагаемого гео- метрического фокуса. Это смещение связано с тем, что фаза дифракционных коэффициентов на апертуре хотя и слабо, но все таки изменяется. Это и приводит к изменению направления лучей (правда в этом случае надо определить понятие луча).

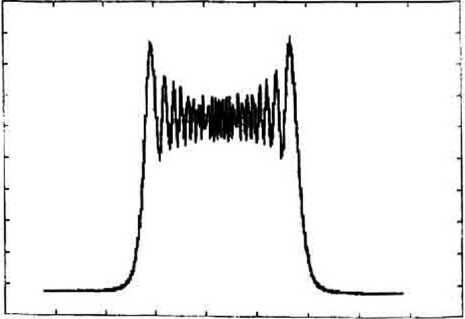
Более сложным примером оптического излучения является фокусатор в отрезок. На рисунке 3 приведены примеры фокусировки в отрезок при различных параметрах.

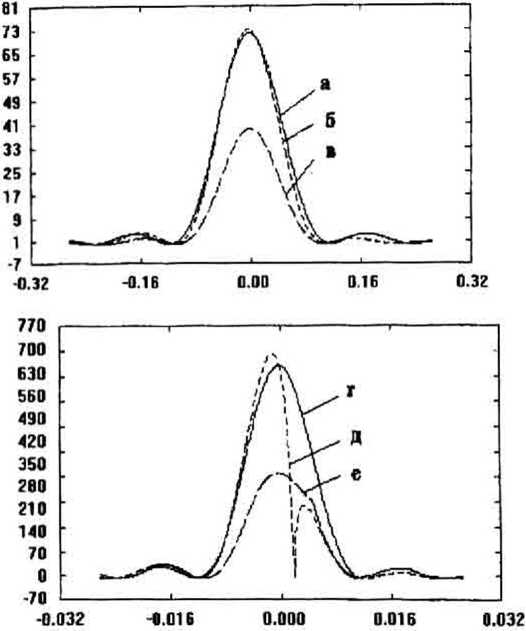
Рис. 2

а) со = 45, р = -25 , f= 100мм, 1>=10мм 6) со = 45 , р = -15 , ]=100мм, В= 10мм в) со = 45, р = 0 , f= 100мм, D=10mm г) со = 45, р = -25 , ]=20мм, В=10мм д) со = 45, р = -15 , /=20мм, П=10мч

е) со = 45, р = Q , /=20мм, 1)=10мм

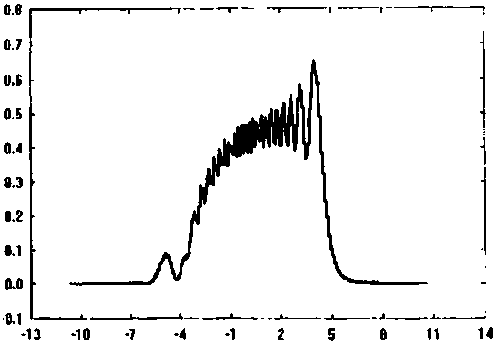
Рис. 36

со =45 ^ = -15 ^_1QOmm> d=iomm , L=10mm

-13     -1U     -7      -4      -1       2       5       8      11      14

Рис. Зе

СО = 45 _fP = 0 ,/=Ю0мм, D=10mm ,1=1 0мм

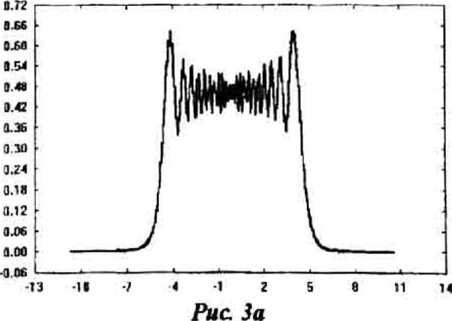
со = 45, р = -25 ,/=100мм, В=10мм , размер отрезка

L-IOmm

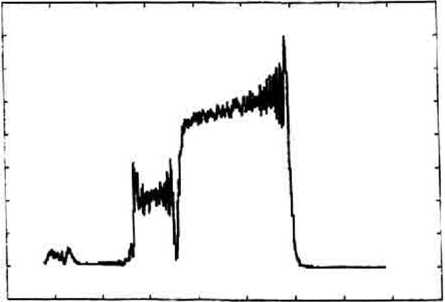
18 0.7 0.6 lb 0.4

13 0.2 11 10 -0.1

-13 -18 -7 4 1 2 5 8 11 14 Рис. Зг со = 45, р = -25 ,/=10мм, D=10mm, L=10mm

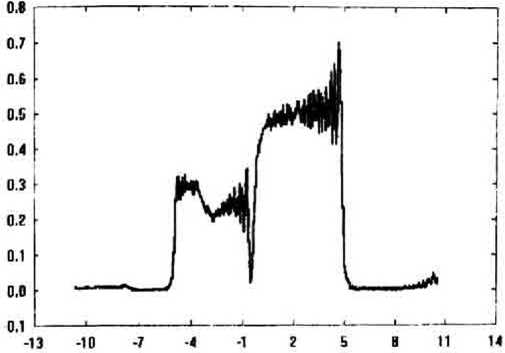
Рис Зд щ = 45,/^=-15 ,f= 10мм, D=10мм, L=10mm

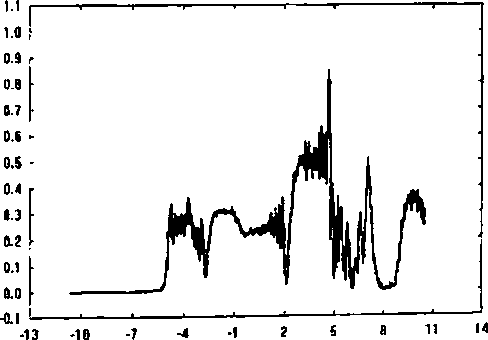
Рис Зе со = 45, р = 0 ,/=10мм, D=I0mm , L=10mm

Дифракция на квазипериодических одномерных структурах в электромагнитном приближении

Рассмотрим отражение плоской электромагнитной волны от идеально проводящей квазиперио-дической структуры. Пусть плоская волна exp(z^(«oxv -PtxN +^г)) падает на одномерный оптический элемент (см рис 4),. границы зон хт, ко торого определяются из уравнения

Ф<хД = тХ т = \,1......

Чтобы упростить рассуждения рассмотрим одномерный случай. Введем систему координат ^хп>^хм^^хт • И вектора

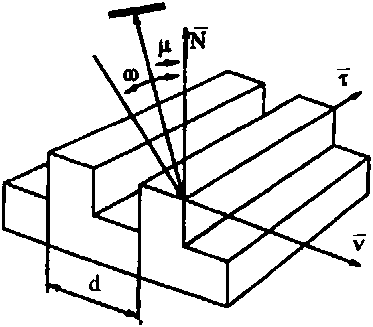
Рис 4 Падение свопа под углом на бинарную отражательную квазипериодическую структуру s - определяет направление распространения

N - вектор нормали к решетке (к плоскости) v - вектор нормали к линиям решетки г - вектор касательный к линиям решетки т = [и х Aj - Vp(u)

вектор перпендикулярный к ли ниям решетки и лежащий в плоскости оптического элемента.

Введем также вектор / лежащий в плоскости падения волны (т.е в плоскости проходящей через вектор нормали к плоскости оптического элемента и вектор падающей волны ) и вектор t перпендикулярный плоскости падения.

- _ v х TV j - _ sxf] sxAI’ s х 7] ’

В падающей волне

£ = £,+£, (24)

Рассмотрим случай, когда электрический вектор лежит в плоскости оптического элемента

Ё = ехр^(^х + svy + s,z)]f ,(25)

Н = — \grad exp[/^(sx)]x t ]

ik.                           ,(26)

Составляющая электрического поля вдоль штрихов в падающей волне

£?=('•?)•(28)

Составляющая магнитного поля вдоль штрихов в падающей волне

ЯГ°=М-<

Если вектор магнитного поля параллелен плоскости оптического элемента

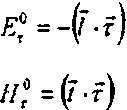
Компоненты электромагнитного поля можно найти используя следующие выражения

Ё = E_vv*E_nN + ЕД , Н = НД - H_nN + НД , (32)

Е^Д-Д^н.-гг.Е?, En = "  _k^_y^ v^Ht *^'^Е^ H_v = "- £^2^ ^ "У^Н^ ^Н«=1^7р.Е,*7бкН^

Рассмотрим зону с номером т, расположенную в интервале [xm, хт+] ]. Будем полагать, что поле в этой зоне при z=0 совпадает с полем дифракционной решетки, у которой микрорельеф на периоде совпадает с микрорельефом в данной зоне и структура микрорельефа во всех зонах подобна с точностью до масштаба. В этом случае все характерис тики выходного поля (коэффициенты дифракции)

Л зависят только от соотношения —. d

Используя формулы (33) получим выражения для отраженного от решетки поля

^(х) =p_r°|exp(r^ox_v +/£ух_г )£££”„ ехр(/'£ —(x_v - x_m^ikp_nx_N>ect(x_m1x_m^y т п

Н_Т (х) = |/7_г°|ехр(^а_ох„ + ikyx_t )£ £Н^т„ exp(jky(x_v - х_т) + ikp_nx_N >ectm ,x_m+!),

^ЕЛ^ = "тЦ- ^r⁰ expO^x, ^кух5£^Р_пН^т„ exp(ik^-(x_v -х_го^1кр_пх_КУес1<х_го,х_т^*

+yE_t° exp№z_ox_v + ikyx_t^^a_nE^m_n exp(ik^-(x_v-x_m)+ikp_nx_Nyect(x_m,x_m4

H_v (*) = T-Ц" ^E.° expO^x, + ikyx_t)££p_nE^m„ exp(ik^-(x_v - x_m) +ikP_nx_N >ectm, x_m+l)- m n              d_m

-yHrc exp(ikaoxv + ikyx, )£ anH m„ exp(ik(xv - xn) + ikp„xN >ect

^En^ ⁼ 7^4 ^ expOka_Qx_v +ikyx_T^>„H^m„ exp(ik~(x_v -x_m)+ikp_nx_Nyect(x_m,x_m+v)-

-yE_T° exp(.ika_ox_v + ikyx, )££p_nE^m„ exp(ik~(x_v-x_m) +ikp_nx_Nyect(x_m,x_m+])

^Hn^ ^{= -}TT7"\^E^^e^ka₆x_v ^ikyx^^a^n exp(ik^-(x_v-xJ-Hkp_nx_Nyect(x_m,x_m^) +

+yH;exp(ika_ox_v^ikyx_T^^P_nH^mnexp(iky-(.x_v-x_m')+ikp_nx_Nyect(x_m>x_mJ где

/(«) = (»•?(«)), а₀(н) = (?.у(и)), ^(«)=_tto(i/)+—, d

Pn(«)=Vi~/²(“)-«»(»), % = |vp(«)|.

Учитывая

V^ = 2/^„, p(x) = mA+Vp(x-xJ, получаем выражение для поля формируемого оптическим в плоскости xN = О

^>tx) = ~(i_z^^^r (“)Яп(")/^м) + /(“)£г0(“)£„(^             exp(iJSu),(41)

Hv ^Х) = Q-yi^Zk W-nWPn(uVy

^En^ (i-yi^Zk WlДкуц^ y(u)£_r°(w)£_n^p_n(м)}ехр(/Аир(ы)) ехр(Ивй'),

//у(х) " (1_z2)Z{E'r (“)/„(“)«„(.«) /(«y/r°(u)//„(u)^(u)}exp(j*?^(M))exp(^i7),                      (43)

^E; (x) = £ E, °кП)Е_п ^) ехр(Иотф(й)) схр^й).

нA5) = ТА°1й)Нп(й) ехр(Ипф(и)) expQUsu-).

Полученные формулы получены для дифракции на одномерном дифракционном оптическом элементе, но их вид как нетрудно заметить остается неизменным и в случае двумерного дифракционного оптического элемента.

Для нахождения электромагнитного поля во всем пространстве необходимо воспользоваться представлением поля в форме Кирхгофа-Котлера. Вычисление интеграла Кирхгофа-Котлера представляет собой сложную вычислительную задачу, так как в общем случае нельзя воспользоваться алгоритмами БПФ. Авторами для вычисления данного интеграла был использован метод Гопкинса. Этот метод рекомендуется использовать в случае когда функция ^(х, у) является дифференцируемой. Кроме того для уменьшения времени расчета был использован модифицированный метод. Модификация метода состояла в том, что при расчете методом Гопкинса отбрасывались члены в интегральной сумме, если аргумент в функции sin с(х) превышал 10. В этом случае в этих точках отпадала необходимость расчета дифракционных коэффициентов и произведений векторов, вычисление которых занимает большую часть времени.

В .заключение вычислим поле от “линзы”.

Рассмотрим оптический элемент, границы зон которого описываются функцией.

ф(х) = х sin о) + ^(х-Убшд)² +>²+/²cos² д -(46)

Внутри зоны микрорельеф имеет вад бинарной дифракционной решетки с одним штрихом.

Нетрудно заметить, что данный элемент фокусирует излучение в точку с координатами

(/ sin д,0,/ cos д)-. (47)

Результаты вычисления поля приведены на рис. 5.

Результаты были получены для случая когда вектор магнитного поля лежит в плоскости оптического элемента.

Анализируя полученные результаты можно видеть, что при коротких фокусных расстояниях наблюдается асимметрия формы фокального пятна.

Рис. 56

Рис. 5в

(О = 45, д = 0 ,/-100мм, D-10 xIOmm

Рис. 5г to - 45, и = -25 ,(=20м.м, D -JOxJOmm

*

#

Рис. 56

ш = 45, д = -15 J=20mm. D 10 xIOmai

Рис. 5е to = 45, ц = 0 , f 20,мм. D 10 хЮ.мм

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 96-15-96026)