Расчет поправки на поглощение в рентгеноспектральном микроанализе

Современные электронно-зондовые микроанализаторы комплектуются фирменным программным обеспечением, в которое входит программа, для учета, матричных эффектов. Учет матричных эффектов, применяемый для коррекции неисправленных содержаний, выражается в виде ряда, независимых факторов: поправкой на. поглощение рентгеновского излучения, поправкой на средний атомный номер, поправкой на обратное рассеяние и поправкой на. флуоресценцию. Если по отношению к нахождению последней поправке на. сегодняшний день особых разногласий нет, то по отношению первых трех приемлемое согласие отсутствует.

В большинстве случаев, наибольшая коррекция требуется для анализа эффекта поглощения рентгеновского характеристического излучения. К настоящему времени разработано множество методов нахождения поправки на поглощение. Большинство из них основано на использовании функции

— распределения генерированного электронным зондом рентгеновского излучения по массовой толщине образца ( р — плотность образца, z — координата по оси, направленной перпендикулярно поверхности вглубь образца, начало координат в точке пересечения оси с поверхностью, pz — массовая толщина). Такой подход использован в моделях, предложенных Лавом и Скоттом [1], Данкабом [2], Пушо и Пишуаром [3, 4], Габером [5] и др. Методы вычисления ^(pz) по-существу представляют собой методы аппроксимации экспериментальных или теоретических данных «удобной» для использования функцией.

В настоящей работе представлены результаты, полученные при разработке новой аналитической аппроксимации функции ^(pz), которая обеспечивает хорошее соответствие расчетов с экспериментальными данными для всех материалов от бериллия до астата. [6].

Поглощение рентгеновского излучения внутри образца часто вносит наиболее значимый вклад в величину матричной поправки и его совершенно необходимо учитывать при количественном анализе. Общее выражение для коррекции на. поглощение обозначается как F а или /(у), где

∞

/ ( У ) = /

^(p^exp-Xpi^Wp^/

∞

p(pz)d(pz).

у определяется выражением у = Ц^{cos ес}(Ф)>^гД^е Ц ^— массовый коэффициент ослабления рентгеновского излучения в веществе образца, ф — угол выхода излучения из образца.

При возбуждении рентгеновского излучения пучком моноэнергетических электронов, энергия которых Еобольше критической энергии возбуждения Ес используемой спектральной серии, функция p(pz) может быть представлена в виде суммы двух слагаемых [7]:

Р ⁽pz) = P 1 ⁽p^z) + P2⁽pz), где

P 1 ⁽p^z)=P 1 (z p + |pz — Z p|) ,                                    (3)

здесь zp - наиболее вероятный пробег электронов в веществе образца.

Распределения поглощенных p1(pz) и обратно рассеянных p2(pz) электронов имеют вид соответственно [6]:

( ,^{(1 -} 7 1 —⁰,⁴³7 2 ) к J    ^{(pz - pz} p ⁾² 1

^P1(pz)          H        ^ ^E 0 ^exp| p2 z p +_a p ²z p zj ,                  ⁽⁴⁾

• 1,    08577 1          J (pz — pz ssV)

P2(pz) = —--Eoexp < - ------- A                   (5)

V " ztr                     ^pz ss

7 1 и 772 — интегральные коэффициенты обратного рассеяния электронов, испытавших единичное упругое рассеяние и вышедших из мишени и испытавших многократное рассеяние в образце соответственно, z _ss и z_tr ~ глубины максимальных потерь энергии обратно рассеянными электронами и первичными электронами, испытавшими малоугловое рассеяние и поглощенные мишенью, Ео [кэВ] — энергия пучка первичных электронов, p — плотность мишени, zp = 0, 77 • z_tr — значение наиболее вероятного пробега поглощенных электронов, испытавших многократное рассеяние в образце; Z — средний атомный номер материала образца.

Первое слагаемое выражения (3) определяет вклад в генерацию рентгеновского спектра анализируемой линии поглощенных электронов пучка, испытавших многократное рассеяние в образце и участвующих в ионизациях соответствующей атомной оболочки вплоть до энергии Е = Е_с. Второе слагаемое описывает вклад обратно рассеянных электронов, которые испытали однократное рассеяние на большой угол и в результате покинули объём образца со средней энергией (Е ) = (1 — Z ^1/3) Е0 [8].

В показателе степени p1(pz)nepBoft части выражения (5) содержится параметр а, который зависит от элементного состава образца и энергии электронного пучка. Зависимость а от отношения величины максимального пробега Ry [9] электронов пучка в образце к величине zp может быть представлена в виде а = 1 — exp (—(Rp/3, 63zp)6,67) .                              (6)

При Ео = 20 кэВ для 79А11 величина Ry z_p = 6.42 11 значение а = 1, 0: н.тя 13АІ при Ео = 20 кэВ величина Ry/ z_p = 2.29 11 а = 0,045. Учет нового параметра, а позволяет точнее описывать спад распределения функции р (pz) вглубь образца для материалов с низкими значениями среднего атомного номера. При многократном рассеянии первичных электронов в исследуемом образце после прохождения расстояния, равного примерно транспортному пробегу z_tr, любые направления движения для них становятся равновероятными. Часть электронов, отклонившихся от первоначального направления на 180°, испытает обратное движение в направлении к поверхности. При этом вероятность потерять часть энергии на ионизацию для них возрастает [10]. Этот процесс ответственен за формирование максимума, распределений плотности энергетических потерь поглощёнными электронами и максимума интенсивности p1(pz), генерируемого ими рентгеновского характеристического излучения, на глубине z_p = 0, 77 • z_tr. Поэтому и распределение энергетических потерь поглощенных электронов и соответствующее ему распределение интенсивности излучения по глубине должны быть практически симметричными относительно наиболее вероятного пробега электронов z_p.

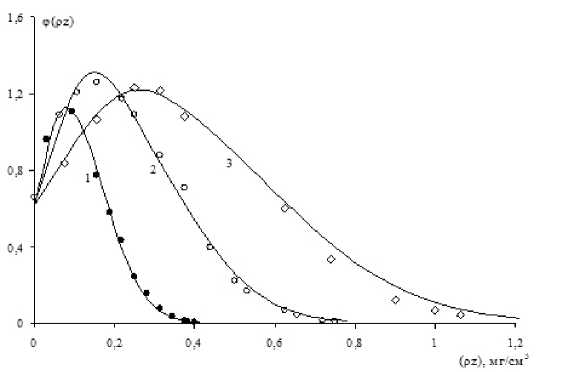
На рис. 1 представлена функция p(pz), рассчитанная по формулам (2) - (6) для различных значений энергии электронов и сравнение ее с экспериментальными данными из работ [11-12], полученными методом «меченого слоя».

Рис. 1. Функция распределения интенсивности излучения по глубине р (/«)для алюминия при нормальном падении пучка, с энергиями: 1-10 кэВ, 2-15 кэВ и 3 - 20 кэВ. Расчеты проведены по формулам (3) - (6) (сплошные линии). Экспериментальные данные (точки), получены методом «меченого слоя» в [11, 12]

Для ізА1 при энергии пучка электронов 10, 15 и 20 кэВ отклонения минимальны и составляют 0,02, 0,04 и 0,04 кэВ•мкнесоответственно. Для 29CU и 79AU средние отклонения составляют 0,08 и 0,11 кэВ•мкм-1.

В результате проведенных исследований получено аналитическое выражение для функции распределения по глубине, генерируемого пучком электронов характеристического рентгеновского излучения, учитывающее: среднюю энергию обратно рассеянных электронов, влияние неупругого рассеяния электронов пучка на распределение p(pz) в образцах с низким значением среднего атомного номера, пространственную симметрию протекания процесса многократного рассеяния относительно положения координаты максимума z_p распределения рЦрг) поглощенных электронов пучка.

Проведено сопоставление модельных расчетов данной функции с экспериментальными данными, имеющиеся в научной литературе [И-12] , которое показывает хорошее соответствие расчёта эксперименту.

Полученные результаты дают основание надеяться, что данная модель функции р(Рг) будет востребована, в практике рентгеновского микроанализа, для учета, матричных поправок и повысит эффективность количественного описания информативных сигналов при исследовании различных материалов, проводимых с помощью хорошо сфокусированных электронных пучков.

Работа, проводилась при финансовой поддержке Министерства, образования и науки Российской Федерации с использованием оборудования Центров коллективного пользования МФТИ и НИЦПВ и при частичной финансовой поддержке Российского фонда, фундаментальных исследований (проект № 10-03-00961).