Расчет преломляющего оптического элемента для формирования заданного распределения освещенности при протяженном источнике излучения

Расчет оптических элементов для формирования заданного распределения освещенности является важной задачей, возникающей при проектировании автомобильной светотехники [1–3], систем подсветки жидкокристаллических мониторов [4,5], систем освещения и т.д. Использование светоизлучающих диодов в светотехнических устройствах становится все более масштабным в связи с увеличением их светового потока и уменьшением стоимости.

При проектировании оптических головок светодиодов задача состоит в расчете внешней преломляющей поверхности головки светодиода из условия формирования заданного распределения освещенности в некоторой плоскости. При точечном (компактном) источнике излучения указанная задача сводится к решению нелинейных дифференциальных уравнений в частных производных типа уравнения Монже-Ампера [6,7]. Решение данных уравнений является сложной задачей. Аналитические решения известны только для частных случаев поверхностей с радиальной или цилиндрической симметрией [8-15]. Для расчета сложных, нерадиально-симметричных оптических поверхностей (в англоязычной литературе – free-form) используются оптимизационные итерационные процедуры, требующие больших временных и вычислительных затрат [16-24]. Работоспособность итерационных процедур [16-24] является недостаточной. Задача расчета преломляющей (отражающей) оптической поверхности для формирования постоянной освещенности в прямоугольной области с большим угловым размером по-прежнему является актуальной.

В работах [17,18] рассмотрен метод расчета преломляющих поверхностей, основанный на численном решении уравнения Монже-Ампера. Метод позволяет создавать сложные распределения освещенности, например, в виде букв. В расчетном примере в [18] буквы формируются на равномерно засвеченном фоне.

Это связано с требованием непрерывности заданного распределения освещенности. Освещенность фона составляет порядка 30 % от освещенности в зоне букв, что существенно снижает световую эффективность. Примеры расчета преломляющих поверхностей для формирования практически важных прямоугольной и эллиптической областей в [17,18] не рассмотрены.

В работах [21–23] представлены градиентные методы расчета преломляющей поверхности для формирования заданного распределения освещенности при точечном и протяженном источниках излучения. Методы основаны на оптимизации функции эйконала, заданной в прилегающей к оптическому элементу плоскости, и последующем восстановлении преломляющей поверхности по распределению эйконала. Приведенные в работах [21–23] примеры показывают хорошую работоспособность метода для источников, излучающих в небольшие телесные углы (порядка π /5 – π / 2 стерадиан). Как правило, реальный источник излучает в полусферу (светодиоды) или сферу (лампы накаливания). Для эффективного использования излучения источника необходимо перераспределять весь его световой поток в освещаемую область.

Наиболее развитый метод расчета преломляющей поверхности представлен в работе [24]. Расчет преломляющей поверхности в [24] основан на решении нелинейной системы уравнений. Метод требует задания функции лучевого соответствия между угловыми координатами исходящих из источника лучей и координатами лучей, попадающих в область регистрации. В работе [24] не предложен общий способ задания функции лучевого соответствия, что ограничивает область применения метода. Тем не менее, метод [24] позволяет формировать заданное распределение освещенности в прямоугольнике и правильном восьмиугольнике с высокой эффективностью и равномерностью.

При проектировании систем подсветки дисплеев большую роль играет толщина системы, определяемая как расстояние от источника излучения до освещаемой области. При уменьшении толщины системы увеличиваются угловые размеры освещаемой области. При этом возрастают френелевские потери и на преломляющей поверхности могут появляться зоны, в которых происходит полное внутреннее отражение. В расчетных примерах, приведенных в [18, 21-24], отношение размера освещаемой области к толщине оптической системы не превышает 2,8, что соответствует максимальному угловому размеру освещаемой области 110°. В работах [18, 21-24] не учитываются френелевские потери, и поэтому угловой размер в 110° является почти предельным при таких методах расчета.

В работе [25] представлен градиентный метод, позволяющий рассчитывать преломляющие поверхности, формирующие заданное распределение освещенности при точечном источнике излучения. Метод [25] учитывает френелевские потери на отражение, что позволяет формировать равномерно освещенные области с угловым размером 150° и более. Ограничением метода [25] является требование малости размеров источника излучения. В данной работе представлена модификация метода [25] на случай протяженного источника излучения. Расчетные примеры показывают, что метод позволяет формировать равномерно освещенные области в виде эллипса и прямоугольника с угловыми размерами 145° при протяженном источнике 1×1 мм. Отношение размера освещенной области к расстоянию до нее составляет порядка 6,5, что более чем в два раза превосходит результаты, опубликованные в работах [18, 21-24].

1.    Постановка задачи

Преломляющий оптический элемент ограничен поверхностью r и имеет показатель преломления n ₁ (рис. 1). В начале координат внутри оптического элемента расположен протяженный источник, излучающий в полусферу z >  0 . Оптический элемент находится в среде с показателем преломления n ₂ (рис. 1).

Задача заключается в определении формы преломляющей поверхности r из условия формирования в выходной плоскости z = f заданного распределения освещенности E ₀ ( u ) , где u = ( u , v ) - де-картовые координаты при z = f .

Пусть преломляющая поверхность описывается функцией радиус-вектора r ( ф , у ) в виде:

r ( ф , у ) =

( x ( ^ф , V ) ) y ^(ф , ^у

I Z ( ф , V ) J

' r (ф, у) sin Ф cos V r (ф, у) sin ф sin у , v r (ф, у) cos ф     ?

где ф и V - углы сферической системы координат. Предполагается, что функция r ( ф , у ) является параметризованной и ее вид полностью описывается вектором параметров c = ( c 1 , c 2 ,..., c_N ) :

r ( ф , у ) = r ( ф , у ; c ) .                                (2)

В таком случае задачу расчета преломляющей поверхности (2) можно рассматривать как задачу оптимизации с параметрами c_i .

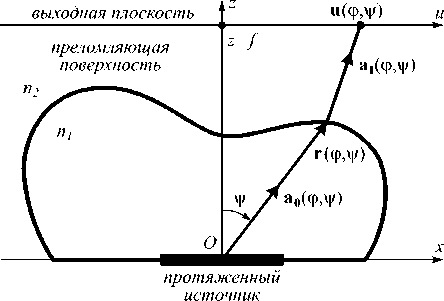
Рис. 1. Схема расположения оптического элемента, протяженного источника излучения и выходной плоскости

В этой работе функция r ( ф , у ) представляется в виде бикубического сплайна. Его параметрами являются значения радиус-вектора и его производных в узлах сплайновой сетки [26]. Ниже, в расчетных примерах, используется сетка (ф i , у j ) , ф i = i л/4, i = 0,1,...,8, у j = j л/ 7, j = 0,1,...,7. Она имеет 64 узла, что соответствует 256 параметрам оптимизации (64 значения радиус-вектора, 128 значений его первых производных и 64 значения смешанной производной). В случае формирования симметричных распределений освещенности в прямоугольной или эллиптической области достаточно определить функцию r ( ф , у ) только в первом квадранте. Это позволяет более чем в четыре раза снизить количество параметров оптимизации.

2.    Модификация метода расчета преломляющей поверхности

Рассмотрим метод расчета, представленный в [25] для случая точечного источника излучения. Метод [25] заключается в градиентном поиске параметров преломляющей поверхности, обеспечивающих формирование заданного распределения освещенности. Минимизируемой функцией в [25] является среднеквадратичное отклонение формируемого распределения освещенности от заданного

^e(c)=N и^ ( E ⁽ u ; ^{c )-} E о ^{( u} ) ) ^{d u d v} ,         ⁽³⁾

где || S || – площадь области S , в которой задано требуемое распределение освещенности E 0 ( u ) . Функция E ( u ; c ) в выражении (3) представляет формируемое распределение освещенности, рассчитываемое по формуле [25]:

E (u; c ) = JJI (ф, ф) T (ф, ф; c )x

D

( s i ( ф , ф ) ^{, N} ( ф , ф ; c ) )                              ⁽⁴⁾

^х                    М ^u - ^u ( ф , ф ; ^c ) ) ^d Ф ^d Ф ^,

r2 (ф, ф; c)

где I (ф, ф) - интенсивность точечного источника излучения, T (ф, ф; c) - коэффициент пропускания Френеля при прохождении луча через преломляющую поверхность, s1 (ф, ф) - единичный вектор ис- дr dr ходящего луча, N (ф, ф; c )=—х— - вектор нор-дф дф мали к поверхности в точке r (ф, ф; c), 5а - функция Гаусса, аппроксимирующая дельта функцию, u (ф, ф; c) - точка на выходной плоскости, в которую попадает луч, испущенный источником в направлении (ф, ф). Интегрирование в выражении (4) ведется по области

D = {(ф,ф):фе [0,п/2], фЕ [0,2п]} .

Градиентный поиск осуществляется по методу Бройдена-Флетчера-Голдфарба-Шанно [27]. При вычислении градиента частные производные функции ошибки (3) имеют вид:

де( c)     1                              дE (u; c)

= ^-^Ж ^E ( u ; ^c ) ^{- E} 0 ( u )) ^{хх        d} u ^d v ^{, (5)}

^д C i      e ( ^c ) s                              ^д C i

-15

Рис. 2. Оптический элемент, формирующий равномерное распределение освещенности в эллиптической области от точечного источника где производные дE (u; c)/дci могут рассчитываться аналитически (прямым дифференцированием выражения (4)) или с использованием формул численного дифференцирования.

Рассмотрим случай плоского протяженного источника излучения, расположенного в области G , при z = 0 . В простейшем случае протяженный источник может быть аппроксимирован набором N точечных источников. Выражение для распределения освещенности (4) при N источниках принимает вид:

^E ( u ; ^c ) = ZJJ I i ( ф ^, ф ^, x i ; ^c ) T ( ф ^, ф ^, x i ; ^c ) ^x i = 1 d

_x ( S i ( ф , ф , x i ; c ) , N ( ф , ф ; c ) ) _x

( r ( ф ^, ф ; c ) ^- x i ) 2

x8_a ( u - u ( ф , ф , x i ; c ) ) d ф d ф ,

где I i ( ф , ф , x i ; c ) - функция интенсивности i -го точечного источника, находящегося в точке x i = ( x i , y_t ,0 ) , x i Е G .

В общем случае, протяженный источник описывается функцией яркости B ( ф , ф , x , y ) . В пределе (когда число точечных источников N стремится к бесконечности) сумма в выражении (6) переходит в двойной интеграл по области G

E ( u ; c ) = JJ JJ B ( ф , ф , x , У ; c ) 5 i _z ( ф , ф , x , y ; c ) x DG

( s i ( ф ^, ф ^, x ^, y ; c ) ^, N ( ф ^, ф ; c ) )

^x T (ф^, ф^, x ^, y ; c ) ——----—---- -2— ^x (7)

( r ( ф , ф ; c ) - ( x , y ,0 ) )

x8_o ( u - u ( ф , ф , x , y ; c ) ) d x d y d ф d ф .

Алгоритм градиентного поиска при переходе от точечного источника к протяженному не изменяется. Производные д E ( u ; c )/ д c i в выражении (5) могут быть рассчитаны прямым дифференцированием (7) или численно.

3.    Примеры расчета оптических элементов

Метод расчета [25], модифицированный с учетом выражения (7), был реализован в среде программирования Matlab. Приведем несколько примеров, иллюстрирующих работоспособность метода.

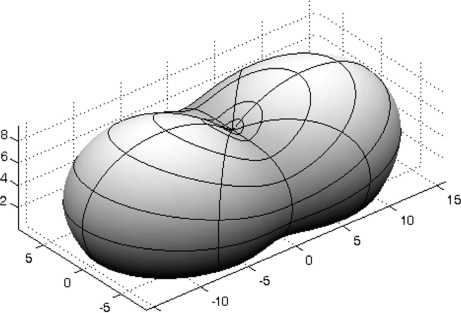
На рис. 2 показан рассчитанный с помощью не-модифицированного метода [25] оптический элемент, формирующий равномерное распределение освещенности в эллиптической области при точечном ламбертовском источнике излучения. Расчет производился при следующих параметрах: коэффициент преломления материала оптического элемента – 1,5, расстояние от источника до выходной плоскости – 15 мм, полуоси эллипса – 50 мм и 25 мм. При данных параметрах отношение большой оси эллипса к толщине оптической системы – около 6,6, что соответствует угловому размеру освещаемой области 146°. Габаритные размеры полученного оптического элемента вдоль осей координат – 30,8×16,6×9,5 мм.

б)    -60         -30          О           30 u,v, лш

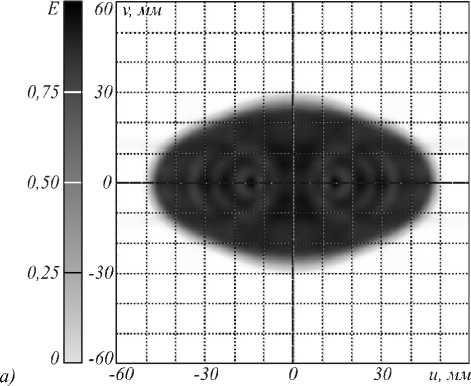
Рис. 3. Распределение освещенности, формируемое оптическим элементом, изображенным на рис. 2, от точечного источника. а) Полутоновое распределение.

б) Сечения распределения освещенности: непрерывная линия – v = 0 , штриховая линия – u = 0

В качестве начального приближения для оптимизации был взят оптический элемент, формирующий равномерное распределение освещенности в круглой области [14]. Сплайновая сетка (определенная в первом квадранте) имела 24 узла, что соответствовало 61 параметру оптимизации (с учетом свойств симметрии). Оптимизация заняла порядка 2 часов на компьютере с процессором Intel® Core™2 Quad 9400 (использовались все 4 ядра). На рис. 3 показано распределение освещенности, формируемое оптическим элементом на рис. 2. Распределение освещенности рассчитано с помощью специализированного программного обеспечения TracePro® [28]. Необходимо отметить, что TracePro® не позволяет решать рассматриваемые задачи оптимизации. В данной работе TracePro® используется только для проверки и подтверждения работоспособности рассчитанных преломляющих поверхностей.

Рассчитанный оптический элемент показывает хорошие результаты при небольших размерах используемого источника излучения. При размерах источника менее 0,4×0,4 мм неравномерность освещенности не превосходит 10 %, энергетическая эффективность остается той же.

Рассмотрим в качестве примера протяженного источника излучения светодиод LUXEON® Rebel LXML-PW51 [29]. Он имеет ламбертовскую диаграмму направленности, а размеры излучающего тела – 1×1 мм. На рис. 4 показано распределение освещенности, формируем ое оптическим элементом, изображенным на рис. 2, и светодиодом LUXEON® Rebel. Распределение освещенности на рис. 4 существенно более неравномерное, чем на рис. 2. ОСКО распределения освещенности от заданного увеличилась более чем в 3 раза и составляет 20,1 %. Таким образом, рис. 4 показывает, что приближение точечного источника при данных параметрах приводит к значительному ухудшению равномерности формируемого распределения освещенности.

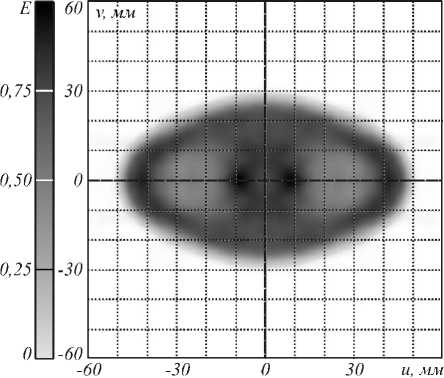
б)

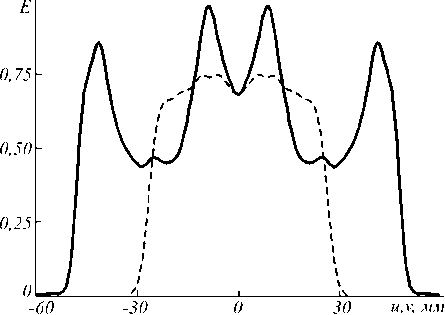
Рис. 4. Распределение освещенности, формируемое оптическим элементом, изображенным на рис. 2, от светодиода LUXEON® Rebel LXML-PW51.

а) Полутоновое распределение. б) Сечения распределения освещенности: непрерывная линия – v = 0 , штриховая линия – u = 0

Рассчитанная преломляющая поверхность была прооптимизирована еще раз для протяженного источника LUXEON® Rebel с помощью модифицированного метода (3), (5), (7). Оптимизация заняла менее часа на компьютере с процессором Intel® Core™2 Quad 9400 (использовались все четыре ядра). Форма и размеры оптического элемента остались практически теми же (максимальное относительное изменение радиус-вектора составило 1,7 % от его первоначального значения). На рис. 5 изображено расчетное распределение освещенности, формируемое дополнительно прооптимизированным оптическим элементом для светодиода LUXEON® Rebel LXML-PW51. Энергетическая эффективность оптического элемента составляет порядка 73,6 %, неравномерность формируемого распределения освещенности – менее 5,7 %. Таким образом, учет размеров источника в виде (7) позволяет достичь такой же равномерности распределения, как и при точечном источнике. Следует отметить, что уменьшение энергетической эффективности по сравнению с точечным источником составляет 7 %. Это вызвано как увеличением френелевских потерь, так и некоторым «расплыванием» распределения освещенности из-за размеров источника.

а)          -60       -30        0        30 и, мм

б)

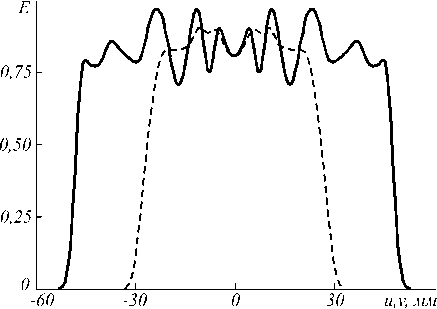
Рис. 5. Распределение освещенности, формируемое дополнительно прооптимизированным оптическим элементом, изображенным на рис. 2, от светодиода

LUXEON® Rebel LXML-PW51. а) Полутоновое распределение. б) Сечения распределения освещенности: непрерывная линия – v = 0 , штриховая линия – u = 0

В качестве второго примера был рассчитан оптический элемент, формирующий равномерное распределение освещенности в прямоугольной области. Размеры прямоугольника – 88×44 мм, остальные параметры такие же, как и в предыдущем примере. В этом случае отношение характерного размера ос- вещаемой области к расстоянию до нее составляет около 6,5, что соответствует угловому размеру 145°.

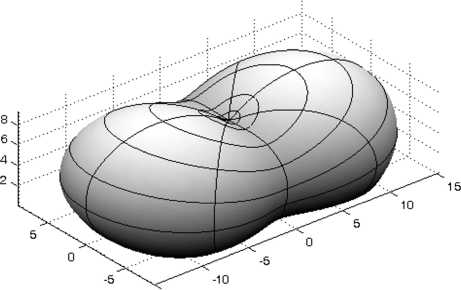
Рис. 6. Оптический элемент, формирующий равномерное распределение освещенности в прямоугольной области от точечного источника

и, ММ

-15

а)

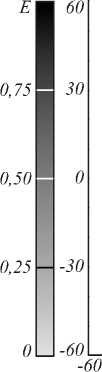
Е

0,75

0,50

0,25

0 —

б)     -60

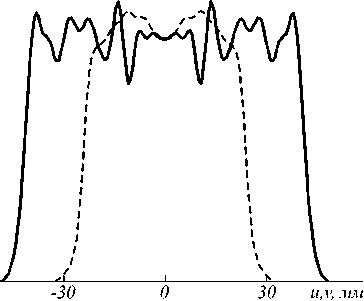
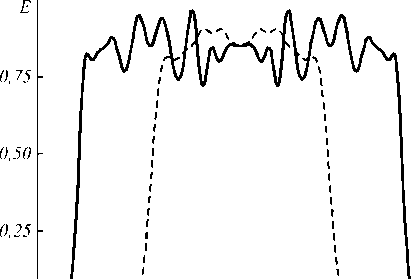
Рис. 7. Распределение освещенности, формируемое оптическим элементом, изображенным на рис. 6, от точечного источника. а) Полутоновое распределение. б) Сечения распределения освещенности: непрерывная линия – v = 0 , штриховая линия – u = 0 .

На рис . 6 показан оптический элемент, рассчитанный для точечного ламбертовского источника излучения с помощью немодифицированного метода [25]. Размеры оптического элемента – 29,6×17,2×9,5 мм. На рис. 7 изображено распределение освещенности, формируемое преломляющей поверхностью на вы- ходной плоскости. Энергетическая эффективность оптического элемента составляет 78,4 %, а неравномерность освещенности – менее 7,3 %.

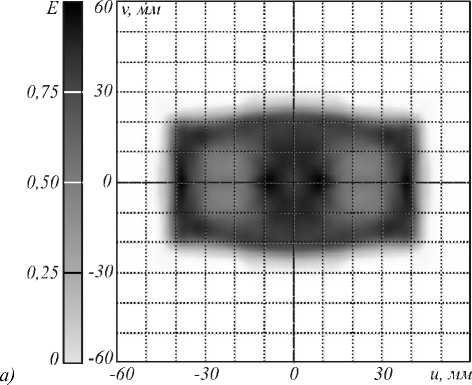
0,75 -

0,25 к

0,50-

u,v, мм

б)     -60

б)     -60

Рис. 8. Распределение освещенности, формируемо оптическим элементом, изображенным на рис. 6, от светодиода LUXEON® Rebel LXML-PW51. а)Полутоновое распределение. б) Сечения распределения освещенности: непрерывная линия – v = 0 , штриховая линия – u = 0 .

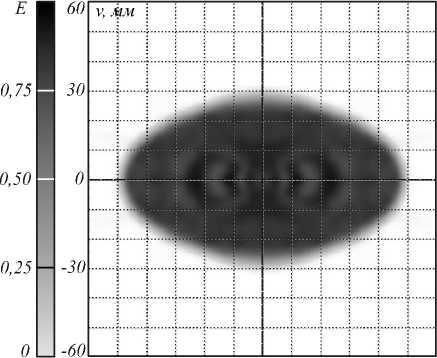
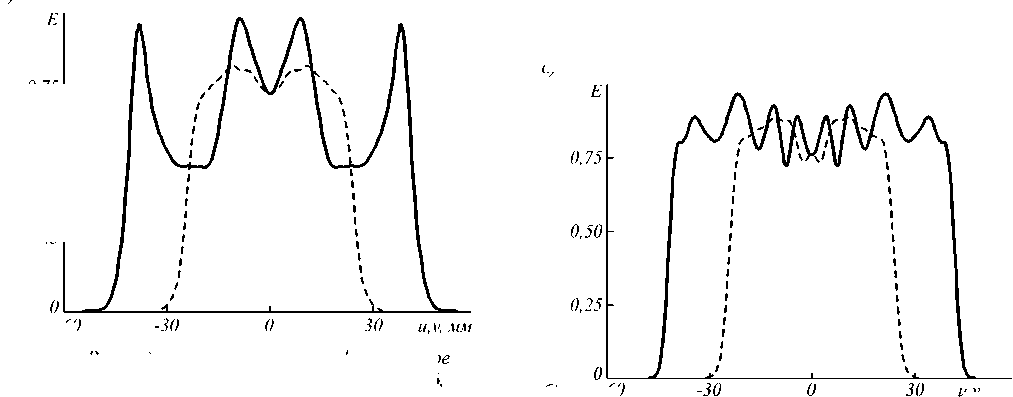
Как и в примере с эллипсом, рассчитанный оптический элемент сохраняет свои рабочие характеристики при размерах источника излучения менее чем 0,4×0,4 мм. На рис. 8 показано распределение освещенности, формируемое рассчитанным оптическим элементом при протяженном источнике излучения LUXEON® Rebel LXML-PW51 (размер излучающего тела 1×1 мм). Распределение освещенности на рис. 8 существенно более неравномерное, чем на рис. 7. ОСКО распределения освещенности от заданного увеличилась более чем в 2,5 раза и составляет 19,5 %. Для уменьшения ОСКО оптический элемент был дополнительно пр ооптимизирован с помощью модифицированного метода (3), (5), (7). Процесс оптимизации занял около часа. Форма и размеры оптического элемента практически не изменились – максимальное относительное изменение радиус-вектора составило 1,5 %. На рис. 9 изображено расчетное распределение освещенности, форми- руемое дополнительно прооптимизированным оптическим элементом при источнике излучения LUXEON® Rebel LXML-PW51. Неравномерность освещения выходной плоскости снизилась до

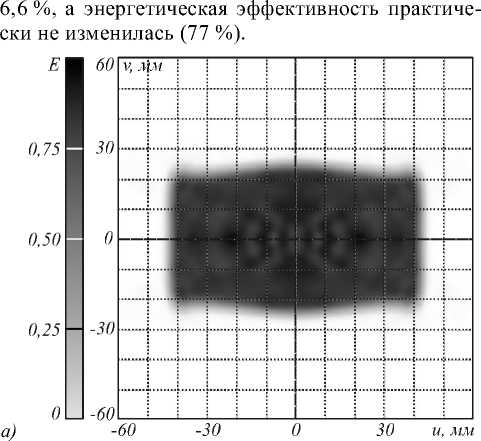
Рис. 9. Распределение освещенности, формируемое дополнительно прооптимизированным оптическим элементом, изображенным на рис. 6, от светодиода LUXEON® Rebel LXML-PW51. а) Полутоновое распределение. б) Сечения распределения освещенности: непрерывная линия – v = 0 , штриховая линия – u = 0 .

Заключение

Метод расчета преломляющих поверхностей, представленный в работе [25], модифицирован на случай протяженного источника излучения. Рассчитаны оптические элементы, формирующие равномерное распределение освещенности в эллиптической (полуоси 50 мм и 25 мм) и прямоугольной (88×44 мм) областях от протяженного источника излучения LUXEON® Rebel LXML-PW51 (размер излучающего тела 1×1 мм). Энергетическая эффективность оптических элементов превосходит 73 %, ОСКО распределения освещенности от заданного – менее 7,5 %. Представленные примеры подтверждают высокую работоспособность метода при расчете оптических элементов, формирующих освещаемые области с угловым размером до 145°.

Работа выполнена при поддержке грантов Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9 и НШ-7414.2010.9).