Расчет приближенно-оптимальных перелетов космического аппарата с двигателями малой тяги с высокоэллиптической на геостационарную орбиту

В настоящее время наиболее распространенной орбитой для размещения спутников связи является геостационарная (ГСО). В большинстве случаев для переводов космических аппаратов (КА) с опорной орбиты на ГСО используются традиционные импульсные схемы, подразумевающие несколько включений маршевого двигателя большой тяги. Однако, в последние годы разработчики КА все чаще проявляют интерес к альтернативным схемам перелетов на ГСО, в т. ч. и схемам, подразумевающим использование на КА комбинации двигателей большой и малой тяги. Причиной этому послужили успешные примеры использования электроракетных двигателей

(ЭРД) на этапах довыведения на ГСО КА AEHF -1, «Экспресс-АМ5», SES -9 [1–3].

Среди множества баллистических схем перелетов КА на ГСО с использованием ЭРД можно выделить три основных:

• 1)    с помощью ракеты-носителя (РН) формируется переходная эллиптическая орбита, при этом радиус апогея орбиты может быть равным радиусу ГСО, а также — больше или меньше его (рис. 1). Функцию довыведения КА выполняет собственная электроракетная двигательная установка (ЭРДУ);

• 2)    формируется низкая круговая орбита с помощью РН, затем с помощью химического разгонного блока (РБ) реализуется переходная орбита. В дальнейшем довыведение осуществляется собственным ЭРД КА, аналогично варианту 1;

• 3)    в третьем варианте РН формирует начальную орбиту, затем с помощью химического РБ формируется переходная орбита. На последнем этапе перелета задействуется многоразовый электрора-кетный транспортный модуль с большой энерговооруженностью [4], который совершает обратный перелет на начальную орбиту.

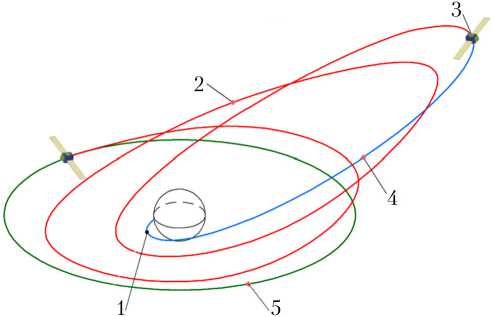
Рис. 1. Баллистическая схема перелета с высокоэллиптической на геостационарную орбиту: 1 — выдача импульса последней ступенью ракеты-носителя; 2 — траектория движения КА с электроракетной двигательной установкой (ЭРДУ); 3 — начало работы ЭРДУ; 4 — переходный эллипс; 5 — геостационарная орбита

В настоящее время в США проводятся запуски геостационарных КА среднего класса, использующих ЭРДУ для выполнения всех динамических операций, включая довыведение КА с геопере-ходной орбиты на ГСО на платформе Boeing -702 SP [5]. В Европе находится на стадии разработки схожая платформа — Electra/ARTES -33 [6]. Аналогом зарубежных космических транспортных платформ среднего класса являются отечественные унифицированные спутниковые платформы «Экспресс-1000» [7] и «Экспресс-2000» [8]. При выведении данных спутников предполагается использование химического РБ.

К настоящему моменту проведены несколько миссий выведения спутников с высокоэллиптической орбиты на геостационарную:

• •    КА SES -8 [9] и Thaicom -6 [10] на РН Falcon 9 v1.1 , перевод которых с переходной орбиты осуществлялся с помощью двигателей большой тяги;

• •    КА SES -14 [11] и AlYah -3 [12] на РН Ariane -5, довыведение которых осуществлялось с орбиты при помощи ЭРДУ.

Высота апогея переходной орбиты в первом случае составляла ~80–90 тыс. км, во втором — совпадала с высотой ГСО.

26 декабря 2014 г. с космодрома Байконур был выполнен пуск РН «Протон» с РБ «Бриз-М» и КА «Экспресс-АМ5». Спутник отделился от РБ на орбите со следующими параметрами: наклонение 0,21°; высота перигея 33 694,66 км; апогея — 37 782,33 км. Дальнейшее движение в точку стояния на ГСО спутник совершил за счет собственных ЭРД коррекции СПД-100 за 73 дня. Изначально разработчики планировали запустить «Экспресс-АМ5» ракетой «Протон» по «южной» трассе, обеспечивающей выведение орбитального блока на опорную орбиту наклонением 48°, но в 2009 г. использование данной трассы было запрещено Казахстаном после запуска DirectTV -12. «Экспресс-АМ5» пришлось перепроектировать на менее выгодную трассу с наклонением опорной орбиты 51,5°. Масса аппарата получилась 3 400 кг, а «Протон» обеспечивал выведение на ГСО лишь 3 250 кг. Это заставило разработчиков КА пойти на довыведение «Экспресса» двигателями коррекции [13].

Схему выведения с использованием круговой промежуточной орбиты можно условно назвать традиционной, поскольку рациональная схема выведения и закон управления движением КА с ЭРД в данном случае хорошо исследованы. Использование промежуточных эллиптических орбит в настоящее время исследовано меньше. Наличие дополнительного баллистического параметра (величина эксцентриситета переходной орбиты) дает расширенные возможности по оптимизации схемы выведения КА на рабочую орбиту. Исследования показывают, что использование эллиптической промежуточной орбиты для многих проектов выведения КА на ГСО эффективнее, чем использование круговых промежуточных орбит. Промежуточная эллиптическая орбита может быть сформирована третьей ступенью РН тяжелого класса («Протон», «Ангара-А5», Delta-IV , Falcon -9, Arian- 5).

Выбору параметров эллиптической орбиты базирования многоразовых буксиров с ЯЭРДУ посвящена работа [14].

Оптимальное значение эксцентриситета промежуточной орбиты может быть достаточно велико, поэтому можно говорить о схеме выведения на рабочую орбиту с использованием высокоэллиптической промежуточной орбиты, в т. ч. и при H _a >  H _ГСО ( H _a — высота апогея орбиты; H _ГСО — высота ГСО).

математическая модель управляемого движения ка

Космические аппараты с ЭРД могут иметь весьма большую протяженность активных участков, поэтому анализ активного участка полета аппаратов с ЭРД проводится на основе полной математической модели в оскулирующих элементах, где ускорение КА от работающей ЭРДУ рассматривается как возмущающее.

Эта система уравнений имеет особенности при e = 0 и i = 0. На практике наиболее распространенным приемом является переход к равноденственным элементам. В данном случае при моделировании движения КА с ЭРДУ обычная система дифференциальных уравнений в оскулирующих элементах является предпочтительной за счет понятных и простых уравнений движения с традиционными орбитальными элементами можно более эффективно сформировать закон управления вектором тяги.

Чтобы избежать особенностей, перед интегрированием будем задавать фиксированные конечные значения эксцентриситета и наклонения, отличные от нуля и соответствующие требуемой точности решения задачи. Следует заметить, что в реальных схемах на первом этапе (дальнего наведения) КА приводится в некоторую область параметров Q по большой полуоси, эксцентриситету, наклонению и долготе стояния. На втором этапе точного наведения устраняются ошибки первого этапа — здесь используются другие математические модели движения, не имеющие особенностей при e = 0 и i = 0.

Уравнения возмущенного управляемого движения КА с непрерывно работающим двигателем малой тяги имеют следующий вид:

dA dt

2 p

(1 – e ) ²

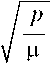
[ e sinϑ S + (1 + e cosϑ) T ],

de dt

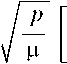
sinϑ S +

e cos²ϑ + 2cosϑ + e

T

1 + ecosϑ di p cosu

= dt µ 1 + ecosϑ dω    1 p              sinϑ(2 + ecosϑ)      esinuctgi

=          – cosϑS +               T –W dt e µ                1 + ecosϑ          1 + ecosϑ dΩ dt

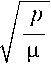
W, sin i (1 + e cosϑ)

sinu du      µpp

=        (1 + ecosϑ)2 –               ctgi sinu W dt       p2                  (1 + ecosϑ)µ dϑ    (1 + ecosϑ)

dt = p p , где p = A(1 – e2) — фокальный параметр; A — большая полуось; е — эксцентриситет; ϑ = u – ω — истинная аномалия; u — аргумент широты; ω — угловое расстояние перицентра от узла; Ω — долгота восходящего узла; i — наклонение орбиты; t — время; S, T, W — проекции возмущающего ускорения на направление радиус-вектора, на перпендикулярное к нему в плоскости орбиты и на перпендикулярное к плоскости орбиты, соответственно; µ = fM — произведение гравитационной константы и массы притягивающего центра.

В качестве возмущающих факторов, помимо реактивного ускорения, создаваемого ЭРД, рассматриваются возмущения, вызываемые нецентральностью поля тяготения Земли, а также возмущения, создаваемые верхней атмосферой Земли

(наличие теневых участков на траектории выведения не учитывается).

В качестве основной возьмем вторую зональную гармонику для потенциала сил притяжения, который при этом имеет вид [15]:

ε

U = –      (3sin2isin2u – 1), сж      3r3

где ε = 2,634⋅10¹⁰ км⁵/с — константа, определяющая сжатие Земли; r — текущий радиус КА.

Составляющие возмущающего ускорения, обусловленного потенциалом второй зональной гармоники, определяются следующими соотношениями [15]:

ε

S_g =      (3sin² i sin² u – 1);

ε

Т_g = –     sin² i sin2 u ;

ε

W_g = –     sin²2 i sin u .

На начальном этапе перелета при низком значении перигея промежуточной орбиты целесообразно учитывать возмущения, вызываемые действием атмосферы.

При разложении вектора аэродинамического ускорения КА по осям орбитальной системы координат TSW можно не учитывать радиальную ( S_f ) и боковую ( W_f ) составляющие аэродинамического ускорения в силу их малости. Тогда выражение для трансверсальной составляющей T_f примет вид:

µ

Tf = СТР "^ (1 + e cosd)²,

Sf = 0, Wf = 0, где ρ — плотность атмосферы; σ — баллистический коэффициент КА, который вычисляется в соответствии с выражением:

CXS

CT =------ ,

m где СХ — коэффициент лобового сопротивления; S — эффективная площадь миделя КА; m — масса КА.

С учетом вышеизложенного проекции возмущающего ускорения S , T , W будут иметь вид:

S = S r + S g ;

T = T_r + T_g + T_f ;

W = Wr + Wg , где Sr, Tr, Wr — составляющие реактивного ускорения КА.

постановка задачи оптимизации и способы ее решения

Упростим задачу управления орбитой. Условия на переменные ω, Ω, u не наклады-dω dΩ du ваются, поэтому уравнения ---, ---, --- dt dt dt могут быть исключены из математической модели вариационной задачи, но при этом учитываться в ходе дальнейшего моделирования (с учетом ограничений на значения e, i).

Сформулируем задачу об оптимальном изменении основных элементов орбиты. В качестве этих элементов примем большую полуось, наклонение и эксцентриситет орбиты.

В качестве критерия оптимальности примем продолжительность перелета T .

Введем две правые системы координат: орбитальную ( Onrb ) и связ_–анную с КА ( OXYZ ) (рис. 2). Вектор тяги p направлен вдоль оси OX .

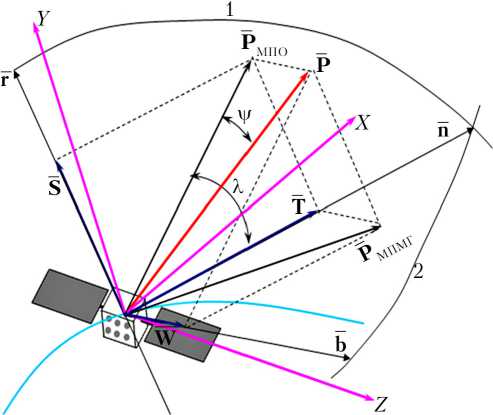
Рис. 2. К определению углов ориентации вектора тяги КА с ЭРДУ: 1 — мгновенная плоскость орбиты; 2 — мгновенная плоскость местного горизонта

Запишем выражения для компонент реактивного ускорения в орбитальной системе координат.

T_r = δ a cosλcosψ;

S_r = δ a sinλcosψ;             (1)

W_r = δ a sinψ.

Здесь a — модуль полного реактивного ускорения ( a = a 0 /(1 - a 0 1 / c )); 5 — функция включения/выключения двигателей (5 = {0, 1}); X — угол между проекцией вектора тяги на мгнове_–нную плоскость орбиты и трансверсалью T (X е [-180°; 180°]); V — угол отклонения тяги от мгновенной плоскости орбиты ( v е [-90°; 90°]) (рис. 2). Очевидно, что при постоянной работе двигателя (5 = 1) время перелета равно моторному времени Т _м.

Управлениями в указанной задаче являются углы ориентации вектора тяги X, V-

При выполнении плоских маневров (изменении большой полуоси и эксцентриситета орбиты) основной вклад вносит трансверсальная составляющая реактивного ускорения T, а при управлении наклонением орбиты используется только бинормальная компонента W, знак которой дважды меняется на витке в соответствии с правой частью дифференциальных уравнений для , содер-dt жащей cosu.

Запишем граничные условия:

t = t ₀               t = t _к

A ( 1 0 ) = A 0 ^ A ( t к ) = A к e ( t ₀) = e ₀           e ( t _к) = e _к

i ( t ₀) = i ₀             i ( t _к) = i _к.

методика, основанная на принципе максимума л.С. понтрягина

Решение вариационной задачи можно проводить в соответствии с принципом максимума Л.С. Понтрягина [16] при условии, что ЭРДУ работает без выключений (5 = 1), поскольку в этом случае обеспечивается минимум общей продолжительности перелета.

Введем сопряженную вектор-функцию Т, составим гамильтониан и найдем его максимум по управляющим функциям X и v :

^Т = ( ^Т A , ^Т е , ^Т i ) T ■

Запишем выражение для гамильтониана в следующем виде:

Н = х/ A1-^ [Л^ + АтТ + A^L µ где

2 А (1 + e )

A S = —(1---)" ⁶ sin^T A + sin^T _е ,

2 А (1 + е )

A_T =---------(1 + е co$3)T +

T (1 - e)                 A ecos2ϑ + 2cosϑ + e

1 + ecosϑ        e, cosu

A W = 1 + e cos S ^

С учетом уравнений (1) выражение для гамильтониана принимает вид:

H =

А (1 - e ²)

Ц

x a [ A S cosXcosv + A T sinXcosv + A W sinv]-

В соответствии с принципом максимума, необходимое условие оптимальности имеет вид:

∂ H

∂λ

I А (1 - e ²) _x ^µ

x a [- A S sinXcosv + a t cos X cos v ] = 0;

∂ H

∂ψ

A (1 - e ²) _x ^µ

x a [- A S cosXsinv — A T sinXsinv + A W cosv] = 0.

Откуда получаем стационарные точки (2):

AT s inλ = ±              ,

А А T + A S

A S cosλ = ±           .

A ² T + A S ²

A_W sinψ = ± _A 2 _{T + A S} 2 _{+ A W} 2

,

A ² T + A S ²

cosψ = ± A _{2 T +} A _{S 2 +} A _{W 2} .

Проверим стационарные точки на экстремум. Для этого составим матрицу производных второго порядка:

∆ =

x 11

x ₂₁

x 12

x ₂₂

^{∂ 2 H} ; x = x    ^{∂ 2 H} ; x = ^{∂ 2 H} .

∂λ2    12    21 ∂λ∂ψ 22 ∂ψ2

Условием экстремума будет отрицательная определенность матрицы производных второго порядка, т. е. одновременное выполнение неравенств

( x ₁₁ x ₂₂ – x ₁₂ x ₂₁) > 0; x ₁₁< 0.          (3)

Таким образом, условиям (3) удовлетворяют стационарные точки (4), в которых достигается максимум гамильтониана.

s in λ

< cosλ

A T

_{A 2 T + A S 2} ,

A S

_{A 2 T + A S 2} .

AW

_{A 2 T + A S 2 + A W 2} ,

sinψ = cosψ =

^{A 2 T + A S 2}

A ² _T + A_S ² + A ² _W ^.

В общем виде сопряженная система уравнений записывается следующим образом:

.

Ψ _A = – _{∂ A} = f_A ( A , e , ϑ, u , λ, ψ, a , Ψ _A , Ψ _e , Ψ _i );

.

Ψ e = – _∂ e = f_e ( A , e , ϑ, u , λ, ψ, a , Ψ _A , Ψ _e , Ψ _i );

.

Ψ = –    = 0, Ψ = const.

i         ∂i

Применение принципа максимума позволяет свести оптимизационную задачу к краевой задаче для системы обыкновенных дифференциальных уравнений. В процессе решения краевой задачи необходимо найти начальные значения сопряженных переменных Ψ _{A 0} , Ψ _{e 0} , Ψ _{i 0} . Отыскание начальных значений обычно проводится с помощью модифицированного метода Ньютона [17], при этом необходимо задавать начальное приближение, которое может быть найдено, исходя из физического смысла этих значений или основываясь на результатах решения упрощенных задач. Применяемый метод позволяет найти оптимальное решение, однако связан с большими вычислительными трудностями и требует высокой квалификации исследователя.

Например, многочисленные результаты решения задач оптимизации межорбитальных перелетов с малой тягой получены В.Г. Петуховым с применением принципа максимума Л.С. Понтрягина [18]. Отмечается, что на первый план в вычислительных схемах решения задач выходит проблема сходимости и устойчивости алгоритма решения краевой задачи и единственности решения.

приближенный метод, основанный на теории локальной оптимизации

В соответствии с принципом взаимности в теории оптимального управления, вариационная задача о минимуме продолжительности динамического маневра с фиксированными граничными условиями эквивалентна задаче минимизации обобщенной невязки по отклонениям терминальных значений компонент вектора состояния при фиксированной продолжительности маневра [19].

Введем терминальный критерий в виде квадратичного функционала, представляющий собой сумму квадратов невязок по большой полуоси, эксцентриситету и наклонению орбиты, умноженных на соответствующие им постоянные весовые (неопределенные) коэффициенты:

I = Δ x _к ^T aΔ x _к → min,           (5)

где Δ x _к = [Δ A , Δ e , Δ i ] ^T . Здесь:

∆ A =

A ( t ) – A _к

A 0

Δ e = e ( t ) – e _к; i = i ( t ) – i _к;

α11 0 0 а = [а у ] = • ) 0 а22 0 0, ^ау = 1, 0 0 α33 где aA = a11, ae = a22, ai = a33 — весовые коэффициенты (элементы диагональной матрицы) по большой полуоси, эксцентриситету и наклонению, соответственно.

Локально-оптимальными управлениями [19] в дальнейшем будем называть такие управления u~(t, x), которые минимизируют не функционал динамической задачи I (интегральный), а подынтегральное выражение, т. е. производную в каждый dt момент времени.

Рассмотрим задачу о минимуме функционала:       _{T d}

I = [--- dt + L ^ min.

0 dt ⁰

Пусть I ₀ > 0. Тогда потребуем выполнения условий:

sign(——) = const; —— ^ max. dt              dt

Очевидно, полученное решение при этом является еще и решением исходной задачи о минимуме функционала I .

Решение при этом получается в виде конечных соотношений, не содержащих неопределенные величины (сопряженные переменные в принципе максимума Л.С. Понтрягина [16]).

Для решения подобной задачи применяются классические методы (в случае, когда область переменных, на которой определено подынтегральное выражение, — открытое множество).

В общем случае синтез локальнооптимальных управлений не гарантирует абсолютного оптимума в исходной постановке задач. Оценка близости локальнооптимального управления к оптимальному приведена в работе Н.Н. Моисеева [19].

Представим систему уравнений в оску-лирующих элементах, описывающую динамику движения КА с двигателем малой тяги, в общем виде:

.

Э = f (Э, au ),               (6)

где a — малый параметр (реактивное ускорение, развиваемое двигателем малой тяги); u — управление, которым в данном случае являются углы X( t ), y( t )•

В силу дифференцируемости функции f перепишем выражение (6) в виде:

.

Э = f (Э, 0) + aBu + 0( a ²),        (7)

где B =

' df (Э, y ) "

∂ y

— матрица частных

y - 0

производных.

Отбросим в уравнении (7) малые второго по _. рядка 0( a ²) и рассмотрим уравнение Э = f (Э, 0). Пусть его полный

интеграл имеет вид:

Э = g ( t , C ).                  (8)

Уравнение (8) может быть рассмотрено в качестве формулы замены переменных. Переходя от переменной Э к C ,

уравнение (7) можно с точностью до величины 0( a ²) заменить:

.

C = a

^{∂ g}

∂ C

-1

Bu.

Рассмотрим функционал:

I (Э( T )) = I ( g ( T , C ( T ))) = I ( C ( T )).   (10)

Задача сводится к поиску минимума выражения (10) при условии (9). Решение этой задачи можно искать в следующем виде:

C = C0 + a C1 + 0(a2), причем C1 удовлетворяет уравнению (11):

C 1 =

∂ g

∂ C

–1

Bu ,

а функционал имеет вид:

I *( C ( T )) = I ( C ₀) + a

dI* dC

С ₁ + 0( a ²).

C = C ₀

Запишем функцию Гамильтона:

H =

^1

∂ g

∂ C

–1

Bu = – a

dI* dC ,

∂ g

∂ C

–1

Bu

Из принципа максимума следует, что управление должно быть выбрано из условия минимума скалярного произведения:

dI*    ∂ g ^–1

dC ^,  ∂ C ^Bu

Теперь найдем локально-оптимальное управление для системы (9). Управление будем выбирать из условия минимума производной

dP (С (T) ) dt

dI* С dI* dC       dC

∂ g ^–1

Bu . (13) ∂ C

Видно, что выражения (12) и (13) совпадают с точностью до множителя, т. е. их минимизирует одна и та же функция u ( t ). Поскольку этот результат был получен для уравнений, в которых были отброшены числа порядка 0( а ²), то можно сделать вывод: локальнооптимальные управления тем ближе к оптимальным, чем меньше величина параметра а .

Приближенно-оптимальные схемы управления вектором тяги ЭРД, основанные на комбинации управлений, максимизирующих производные элементов орбиты А , е , i , описаны в работе [20].

Таким образом, задача оптимального управления большой полуосью, эксцентриситетом и наклонением орбиты в строгой постановке может быть редуцирована до задачи локальной оптимизации.

Будем искать локально-оптимальный закон управления, обеспечивающий совместное изменение большой полуоси, эксцентриситета и наклонения орбиты так, чтобы обобщенная невязка монотонно убывала.

Проведем отыскание локально-оптимального закона совместного управления большой полуосью, эксцентриситетом и наклонением орбиты, обеспечивающего минимум функционала I , определяемого выражением (5), при заданных начальных условиях.

Заменим этот функционал локальным критерием, обеспечивающим максимальную скорость изменения I :

∂ dI

= 0;

d λ dt

∂ dI dψ dt

Результатом поиска максимума dI     dI

=    (λ(t), ψ(t)) по двум переменным dt     dt являются аналитические выражения (15, 16) для углов ориентации вектора тяги λ и ψ, где ψ — угол отклонения тяги от мгновенной плоскости орбиты; λ — угол между проекцией вектора тяги на плоскость орбиты и трансверсалью.

A T *

_{( A T* ) 2 + ( A S* ) 2} ,

A S *

( A _T* ) ² + ( A _S* ) ^{2 .}

dI           1 dA dt = 2a1ΔA A0 dt

+

+ 2a Δ e    + 2a Δ i    → max.

² dt ³ dt

Введем обозначения, учитывая правые части уравнений движения ,    ,    :

dt dt dt

sin ψ =             ^W

^ ( A* ) + ( A* )² + ( a ; )²

( A_T* )² + ( A_S* )² cos ψ =                        .

( A_T* )² + ( A_S* )² + ( A_W* )²

2 A (1 + e )

A * = a Δ A          e sinϑ + a Δ e sinϑ;

^{5     1}     A ₀(1 - e )              ²

2 A (1 + e )

AT * = a1AA -^-(i---— (1 + ecosd) + ecos2ϑ + 2cosϑ + e

+ a₂Δ e                      ;

1 + e cos ϑ

A

*

W

cos u

^{= a 3 Δ i} 1 + e cos ϑ ^.

Тогда функционал записывается в виде:

dI

= 2 dt

A (1 - e ²) ^µ

[ A_S * S + A_T * T + A_W * W ].

Найдем стационарные точки, для чего решим уравнения:

_~ Полученный закон управления ψ^~( t ), λ( t ) имеет достаточно простую структуру и позволяет провести расчет динамического маневра без процедуры решения краевой задачи.

Как следует из выражения (14), от значений весовых коэффициентов a _A , a _e , a _i зависит скорость изменения большой полуоси, эксцентриситета и наклонения орбиты.

За счет подбора значений весовых коэффициентов можно добиться одновременности выполнения конечных условий. В первом приближении можно принять a _A = a _e = a _i .

Сравнение точного и приближенного методов расчетов на модельных примерах

В целях верификации предлагаемого приближенно-оптимального метода расчета проводилось сравнение результатов моделирования с результатами точного

решения задач. На первом этапе апробация метода проводилась на примере перелетов типа «круговая орбита– круговая орбита». В качестве эталона были взяты результаты, приведенные в монографии В.Н. Лебедева [17].

В результате, решение с применением локально-оптимальной программы управления дает несколько отличные значения времени перелета относительно результатов, полученных по методу принципа максимума. Разница составляет 1,2–1,6% (табл. 1).

Таблица 1

результаты сравнения точного и приближенного методов расчетов для перелетов типа «круговая орбита–круговая орбита»

Способ решения	Параметры перелета
	r 0 = 20 000 км r к = 23 350 км A i = 19,022° a = 0,00498 м/с2	r 0 = 50 000 км r к = 58 375 км A i = 19,022° a = 0,00080 м/с2	r 0 = 80 000 км r к = 93 400 км A i = 19,022° a = 0,00031 м/с2
	Время перелета, сут
Приближенный	5,2416	20,648	41,760
Точный	5,1580	20,389	41,264
Отклонение, %	1,62	1,27	1,20

Примечание. r ₀ — радиус начальной орбиты; r _к — радиус конечной орбиты; A i — изменение наклонения; а — модуль полного реактивного ускорения.

Отклонения могут быть вызваны некоторой погрешностью в выполнении граничных условий задачи.

На втором этапе сравнение проводилось на примере перелетов типа «эллиптическая орбита – круговая орбита». Источником для сравнения послужили результаты, приведенные в статье В.Г. Петухова [18]. Конечные значения эксцентриситета и наклонения для всех случаев приняты близкими к нулю, чтобы избежать особенностей при интегрировании уравнений.

Анализ результатов показал, что разница по времени перелета между решениями, полученными с помощью предлагаемого метода, и точными результатами довольно мала и составляет ~0,02–1,00% (табл. 2).

Небольшая величина погрешности позволяет рассматривать локально-оптимальные управления в качестве хорошего начального приближения для решения вариационных задач механики полета с малой тягой.

Таблица 2

результаты сравнения точного и приближенного методов расчетов для перелетов типа «эллиптическая орбита – круговая орбита»

Способ решения	Исходные данные
	r a0 = 42171км r п0 = 6871км i 0 = 75°	r a0 = 42378км r п0 = 6578км i 0 = 7°	r a0 = 46500 км r п0 = 6642,9км i 0 = 7°	r a0 = 34171км r п0 = 6595км i 0 = 63,17°
	r к = 42165км	r к = 42378км	r к = 42378 км	r к = 42160км
	m 0 = 1320 кг I уд= 1500 с P = 0,332 Н	m 0 = 2000 кг I уд = 2000с P = 0,350Н	m 0 = 1500 кг I уд= 1994,06 с P = 0,200Н	m 0 = 776 кг I уд= 1 500 с P = 0,166Н
	Время перелета, сут
Приближенный	171,7303	139,0683	178,1134	193,3796
Точный	170,117	139,0382	177,3602	191,406
Отклонение, %	0,58	0,02	0,42	1,03

Примечание. r _a ⁰ — начальный радиус апогея; r _п ⁰ — начальный радиус перигея; r _к — радиус конечной орбиты; m ₀ — начальная масса КА; I _уд — удельный импульс; Р — тяга.

алгоритм и результаты решения задачи оптимизации перелета между эллиптической и геостационарной орбитами

Ниже приведены результаты расчета довыведения тяжелого геостационарного спутника связи, оснащенного ЭРДУ. Переходная эллиптическая орбита формируется третьей ступенью РН.

Для автоматизации расчетов баллистических параметров перелета КА с ЭРДУ между круговыми и эллиптическими некомпланарными орбитами была разработана программа NEOS .

Для определения оптимальных параметров переходной орбиты с точки зрения минимального времени перелета проведем моделирование с перебором высоты апогея промежуточной орбиты на отрезке г = [40 Оо0; 80 000] для i = 28° и г a = [70 000; 110 000] для i = 51,6°. Исходные данные для моделирования приведены в табл. 3. В расчетах примем массу спутника для всех переходных орбит постоянной ( m ₀ = const).

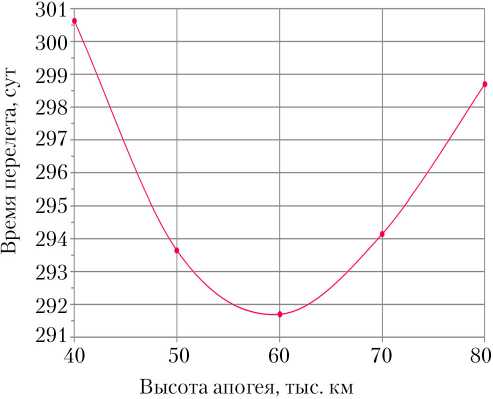
Результаты моделирования приведены на рис. 3.

На следующем этапе исследований планируется провести уточненный анализ с учетом зависимости выводимой массы КА от радиуса апогея переходной орбиты.

Таблица 3

исходные данные для перелета

Наклонение орбиты i , °	Высота перигея Н п, км	Стартовая масса КА m 0, кг	Масса спутника на ГСО m КА, кг	Масса рабочего тела m РТ, кг	Тяга двигателя P , мН	Удельный импульс I уд, с	Диапазон перебора r a, тыс. км
28	200	3 500	2 600	900	360	1 600	40…80
51,6							70…110

a)

Рис. 3. Результаты анализа оптимального радиуса апогея: а — для наклонения i = 28°; б — для наклонения i = 51,6°

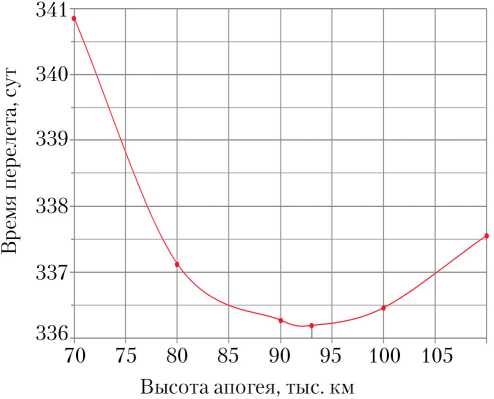
б)

Результаты перебора высот апогея орбиты для двух наклонений выявили оптимальные значения. В случае с наклонением i = 28° оптимальная высота апогея составляет 60 000 км, для i = 51,6° это значение возрастает до 93 000 км. Столь большое различие этого параметра для разных наклонений связано с тем, что весомую часть энергетики перелета на ГСО составляет изменение наклонения орбиты.

В соответствии с правой частью дифференциального уравнения с воз-dt растанием фокального параметра увеличивается скорость изменения наклонения. Таким образом, в нашем случае при увеличении высоты апогея возрастает фокальный параметр, увеличивая при этом скорость изменения наклонения, что приводит к росту оптимального значения высоты апогея высокоэллиптической орбиты с возрастанием угла наклонения исходной орбиты.

Времена достижения необходимого значения каждого элемента орбиты приведены в табл. 4.

Таблица 4

результаты моделирования

i , °	Элемент орбиты	Необходимое значение	Результат
28	e	0	291,22 сут
	А , км	42 164 км	291,61 сут
	i	0°	291,72 сут
	T к	—	291,72 сут
	Масса рабочего тела	—	567,11 кг
51,6	e	0	335,15 сут
	А , км	42 164км	336,19 сут
	i ,°	0	335,56 сут
	T к	—	336,19 сут
	Масса рабочего тела	—	653,56 кг

Примечание. Обозначения приведены в тексте.

Можно заметить, что в результате перелета был истрачен не весь запас рабочего тела. В итоге для случая с наклонением i = 28° остаток составляет 332,89 кг, а для i = 51,6° он составляет 246,44 кг. Излишки рабочего тела могут быть потрачены на продление срока активного существования космического аппарата, а также для его перевода на орбиту захоронения.

Также в результате расчета двух перелетов были подобраны весовые коэффициенты по правилу одновременного достижения элементами орбиты своих конечных значений; они приведены в табл. 5.

Таблица 5

значения весовых коэффициентов

Весовой коэффициент	i , °
	28	51,6
a A	0,082	0,073
a e	0,285	0,456
a i	0,633	0,471

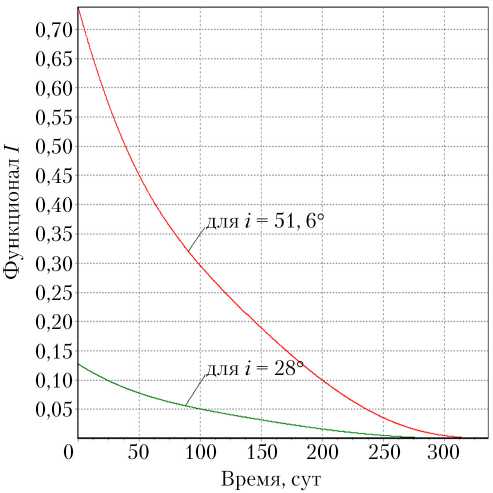
Рис. 4. Изменение функционала I во времени

Некоторое различие во времени достижения элементами орбиты необходимого значения обусловлено погрешностью подбора весовых коэффициентов. Для уменьшения разницы можно провести итерационный подбор весовых коэффициентов.

В ходе моделирования полета КА с учетом воздействия атмосферы Земли значение баллистического коэффициента КА было принято равным 0,00857. Выяснено, что такое воздействие незначительно, так как КА выходит из зоны действия атмосферы уже через несколько витков и находится в ней короткий промежуток времени.

Данный факт можно объяснить тем, что сила аэродинамического сопротивления F_A в нижней точке траектории (наибольшее сопротивление на первом витке) примерно равна силе тяги P ( F A = 320 мН; P = 360 мН), а длительность и протяженность участка воздействия крайне малы. За счет этого высота перигея орбиты выходит за пределы действия атмосферы за 3–4 витка.

В результате моделирования были получены зависимости элементов орбиты и управляющих переменных от времени, представленные на рис. 4–10.

Моделирование показало, что производная функционала не меняет свой знак, а сам функционал монотонно убывает до нуля, минимизируя невязки по большой полуоси, эксцентриситету и наклонению орбиты (рис. 4). Таким образом, обосновано применение метода локальной оптимизации.

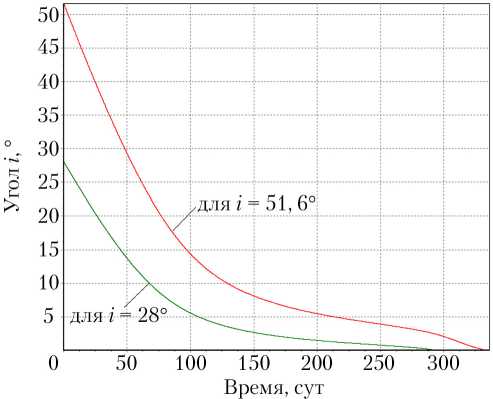
Рис. 5. Зависимость наклонения орбиты от времени

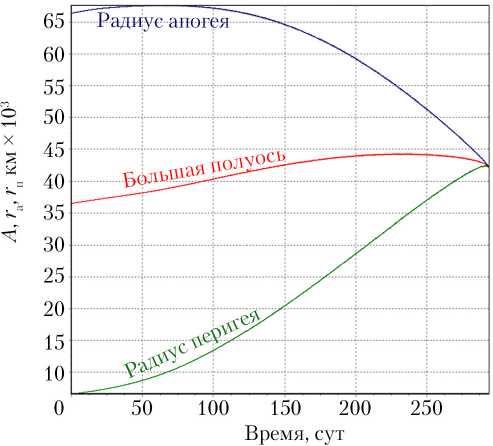
Рис. 6. Зависимость изменения большой полуоси, радиуса апогея и перигея от времени для i 0 = 28 °

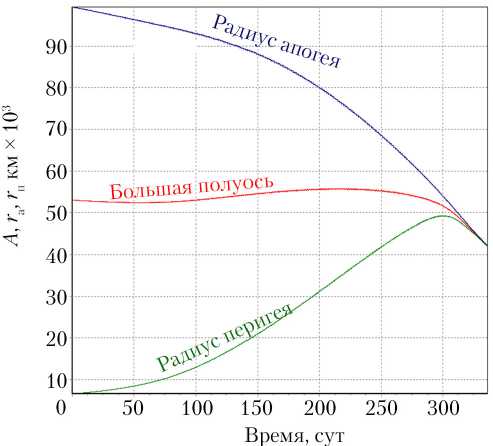
Рис. 7. Зависимость изменения большой полуоси, радиуса апогея и перигея от времени для i 0 = 51,6 °

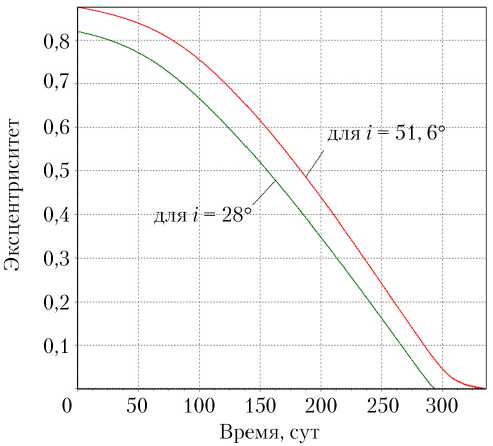
Рис. 8. Зависимость эксцентриситета орбиты от времени

На рис. 9 представлен график зависимости амплитуды управляющего угла у от времени для случая перелета с i = 51,6°. В период 0…250 сут полета видно постепенное монотонное уменьшение амплитудных значений угла у, связанное со скоростью уменьшения наклонения. Начиная от 250 и до 330 сут, наклонение орбиты начинает сначала медленно, а с 300 сут — резко убывать, с чем связано возрастание амплитудных значений угла у. Спад величины амплитудных значений в период с 328 до 336 сут коррелируется с замедлением скорости уменьшения эксцентриситета орбиты.

Зависимость амплитуды управляющего угла у от времени для i = 51,6° приведена на рис. 9.

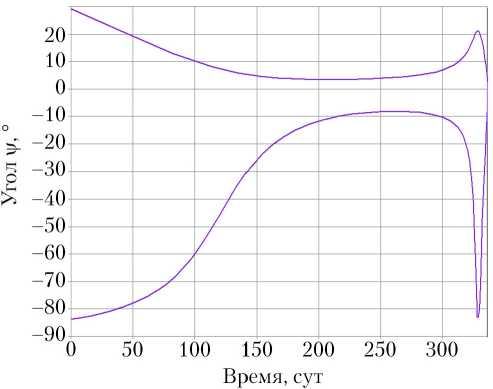
Рис. 9. Линии амплитудных значений управляющего угла для i0 = 51,6°

Зависимость управляющего угла X для случая перелета с i 0 = 51,6° носит колебательный характер, угол меняется в пределах 180^180°.

выводы

Показана принципиальная возможность применения метода локальной оптимизации для расчета перелетов с высокоэллиптических орбит на геостационарную. При этом получены наиболее выгодные значения высоты апогея для случаев перелета с различными наклонениями ( i = 28°; i = 51,6°), рассчитано время перелета и потребный запас рабочего тела ЭРДУ. Также проведена оценка величины влияния атмосферного сопротивления на движение спутника с учетом низких значений высоты перигея ( Н _п = 200 км), приведены графики, отображающие характер изменения орбитальных параметров и углов ориентации вектора тяги ЭРДУ.

Предлагаемый приближенный метод оптимизации удобен для проектно-баллистических расчетов и оценок. С его помощью можно решать целый спектр задач с различными исходными данными и для любых типов замкнутых орбит. Полученные с помощью данного метода результаты могут быть использованы в качестве первого приближения для точных методов решения задачи оптимизации.

Основные задачи, решаемые с использованием довыведения КА на ГСО с помощью ЭРДУ:

• •    обеспечение выведения на ГСО КА увеличенной массы с использованием существующих средств выведения

тяжелого класса (альтернатива созданию новых средств выведения увеличенной грузоподъемности);

• •    обеспечение выведения на ГСО КА с использованием средств выведения среднего класса;

• •    снижение стоимости выведения на ГСО;

• •    обеспечение конкурентоспособности российских геостационарных КА (компенсация северного расположения космодромов);

• •    обеспечение резерва массы геостационарных КА для повышения их надежности и эффективности.