Расчет приборных характеристик времяпролетного масс-спектрометра на основе клиновидного электростатического зеркала с двумерным полем

Масс-спектрометрия является наиболее универсальным методом исследования элементного, химического и изотопного составов вещества. Имеющиеся в настоящее время статические масс-спектральные приборы, как правило, являются стационарными установками больших размеров. В то время как такие области, как экология, геология, нефтегазовые отрасли, медицина, металлургия, материаловедение и космические исследования нуждаются в малогабаритных приборах небольшого веса и размера.

Достоинствами времяпролетного масс-спектрометра (ВПМС) по сравнению с приборами других принципов действия являются: малые габариты и вес, высокая чувствительность, большой диапазон масс, одновременная регистрация всех масс при одном пролете ионного пакета, малое время одного анализа.

В настоящее время основной движущей силой новых разработок ВПМС являются задачи, возникающие в биоаналитической химии: геномика, протеомика, диагностическая медицина, криминалистика, допинг-контроль, фармацевтика. Разработка новых лекарственных средств, их клинические испытания и тому подобные работы требуют выполнения анализов чрезвычайно сложных многокомпонентных смесей и детектирования в них совершенно различных по структуре соединений часто в предельно малых концентрациях. Эти задачи стимулируют разработку приборов, обладающих предельно высокими характеристиками: разрешением по массам, точностью определения массы и динамическим диапазоном масс. Для ис- пользования таких приборов в космосе они должны быть предельно легкими, простыми в использовании, давать надежные и воспроизводимые результаты.

Основным фактором, ограничивающим разрешение простых линейных ВПМС, является энергетический разброс в первоначальном ионном пучке. Среди недостатков этих ВПМС можно отметить также их достаточно большие линейные размеры, обычно порядка нескольких метров. Оба эти недостатка преодолеваются за счет использования ионных зеркал в ВПМС рефлекторного типа.

Во многих ВПМС рефлекторного типа [1] используются однородные электрические поля, создаваемые с помощью мелкоструктурных сеток, что приводит к целому ряду отрицательных последствий, ухудшающих их разрешение и чувствительность. В настоящей работе предложена и исследована схема ВПМС на основе конических зеркал с двумерным полем [2]. В таких зеркалах в области торможения ионов создается почти однородное электрическое поле без использования сеток.

ДВУМЕРНОЕ ПОЛЕ ЭЛЕКТРОСТАТИЧЕСКОГО ЗЕРКАЛА С КОНИЧЕСКИМИ ЭЛЕКТРОДАМИ

На рис. 1 схематически изображено пятиэлектродное зеркало с плоским замыкающим электродом. Точками А, В, С отмечены границы электродов. Рассматриваемая область в плоскости z_n = x n + i y_n отображается на верхнюю полуплоскость плоскости w = и + i v с помощью конформного преобразования [3]:

А

l 1

—*

-1

V 3

V 4

V 3

А

*

l 1

-► хп

Рис. 1. Схематическое изображение зеркала с параллельными электродами.

l ₁ , l ₂ , l ₃ — длины электродов, V ₀ , V ₁ , V ₂ , V ₃ , V ₄ — потенциалы электродов

z n = —arcsin w . π

Откуда

πx πy         πx πy u = sin —- ch —^n-,  v = cos —- sh -^n-.

22   22

Решая соответствующую граничную задачу, найдем распределение потенциала в верхней полуплоскости w -плоскости:

F ( u , v ) = V - F ( u , v\a 3 , V - V ) - F ( u , v|a 2 , V - V , ) -

- F ( u , v|a i , V 2 - V 3 ) - F ( u , v |i, V 3 - V 4 ) .

Здесь а ₁ , а ₂ , а ₃ — параметры конформного преобразования, определенные ниже;

„ /    1 VI u + a

F ( u , v a , V ) =—I arctg----- ' n I v

u - a

- arctg---- v

Конформное преобразование, переводящее границы зеркала с параллельными электродами в границы зеркала с клиновидными электродами

и цилиндрическим замыкающим электродом имеет вид

Z = X + i Y = iexp ( - i a ( z _n + i в ) ) - ictg a .

Откуда

X =—-— e ^ay” sin ax _n , Y =—-— e ^ayn cos ax n - ctg a . sin α               sin α

Найдем также обратное преобразование; пользуя (5), получим

1X xn =-arctgF"——, a Y + ctg a y п=^— In{ |^X2 +(Y + ctga)2 J sin2 a}.

В формулах (5)–(7) учтено, что постоянная

в = 2^   ’    1

2 α sin ² α

.

ис-

В полученном решении замыкающий электрод с потенциалом V ₄ представляет собой выпуклое цилиндрическое зеркало при a >  0 и вогнутое -при a <  0, причем его радиус кривизны определяется выражением

R = sin α

.

Постоянные a ₁ , a ₂ , a ₃ , входящие в (3), выражаются через длины электродов l ₁ , l ₂ и l ₃ зеркала с параллельными электродами ( a = 0) с помощью следующих формул:

а 1 = u ( 1, 1 1 ) = sin ^П ch П 1 = ch ^ ^,

у \ ^п, ^{п (} l i ^{+ 1} 2 )

а 2 = u ( 1, 1 1 + 1 2 ) = sin—ch——- =

^{п (} l i + l 2 )

= ch—------,

а 3 = u ( 1, 1 ₁ + 1 2 + 1 3 ) = sin ^П ch——— ^2—— =

^{п ( 1} i + ¹ 2 + ¹ з )

= ch—--------

.

С помощью формул (6) найдем координаты

точек А, В, С:

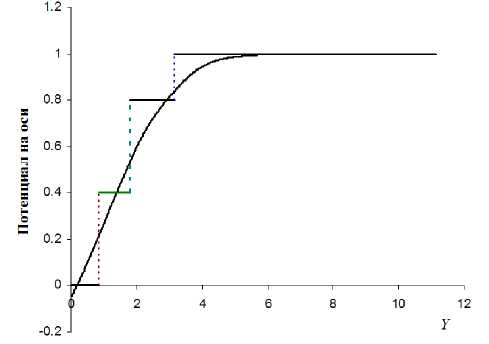
Рис. 2. Распределение потенциала на оси Y

X A = e ^a l , Y a = ( e ^a l - 1 ) ctg a ;

X В = e ^{a ( l1 + 1 2} ) , Y B = ( e ^{a ( 11 + 1 2} ) - 1 ) ctg a ;               (13)

X _C = e ^{a ( 1 1 + 1 2 + 1 3} ) , Y _c = ( e ^{a ( 1 1 + 1 2 + 1 3} ) - 1 ) ctg a .

На рис. 2 представлено распределение потенциала вдоль оси Y и показаны проекции электродов на среднюю плоскость, а на рис. 3 — картина эквипотенциальных линий поля для зеркала со следующими параметрами: a =- 2 ° , L 1 = 0.838, L ₂ = 0.954, L 3 = 1.370, V₀ = 1, V 1 = 0.8, V , = 0.4, V ₃ = 0, V ₄ =- 0.0485 . Здесь длины электродов L 1 , L ₂ , L ₃ зеркала с закругленным замыкающим электродом ( a * 0) определяются формулами:

L =V ( X a — 1 ) 2 ⁺ Y a² ,

L 2 = V( X в — Х а ) 2 + ( Y B — Y a ) 2 ,       (14)

L3 = x X^c — Хв )2 + (Yc — Ya У.

3    C B    CB

На рис. 3 самая нижняя кривая соответствует потенциалу Ф = 0, а самая верхняя — Ф = 0.95 , шаг по потенциалу равен 0.05. Эквипотенциали находились путем интегрирования дифференциального уравнения для эквипотенциалей:

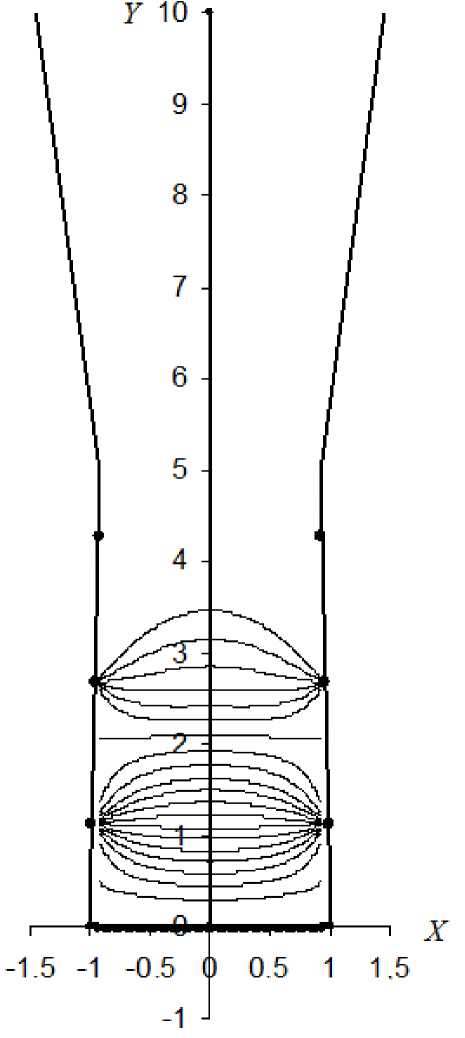
Рис. 3. Картина эквипотенциальных линий поля пятиэлектродного зеркала

d Y    Φ X ( X , Y )

-----=--.

d X Φ _Y ( X , Y )

где индексы у потенциала обозначают частные производные по соответствующим координатам.

Для того, чтобы определить производные потенциала, входящие в уравнение (15), воспользуемся формулами (2), (3) и (4) и найдем производные от функции F1(u,v\a, V). Получим следующую цепочку преобразований:

d F d F д u d F d v

¹ =    ¹      +    ¹     ,               (16)

д X д и д X д v д X д F1 _aF1 д u д F1 д v д Y ”a u д Y д v д Y

.

Здесь, согласно формуле (4):

д F 1 a u

V

= —v π

v ² + ( u + a ) ²

—

v ² + ( u — a ) ² ’

a F 1 д v

V

π

u + a

u — a

--?-+--т" , v2 +(u + a )2 v2 +(u — a )2

д u

I X

д v д u д х„   д u д у„ пп

+                                      , д Y  д xn д X д уп д X

д u д Y

—

д v д u д х„ д u д у„

__                  п ।                   п дх-Ц^д SY дзУТ д7

.

дифференцирование по длине дуги траектории s . Безразмерный электростатический потенциал Ф ^ Ф (х, у) нормирован таким образом, что он равен нулю там, где равна нулю скорость частицы. Индексом 0 отмечен потенциал на входе в систему; ε — относительный разброс по энергии на входе в систему; индексы x и у при потенциале обозначают частные производные по соответствующим координатам. При задании начальных условий для уравнений (26), (27) необходимо учитывать соотношение х11 + у,2 _1. (28)

Согласно [3], в нерелятивистском случае время пролета частицы в безразмерных переменных определяется выражением

В последних выражениях, согласно формулам (2) и (7),

s

1 +2^

Ф J

d s

д u   д v п  п п

---_---_ — cos—x ch—у„ , дxn дУп 2    2 n 2

Г Ф а 2     + е

\ I ^Ф 0

где γ_m — относительный разброс по массе. При

д u д Уп

—

д v   п . п .л

---=—sin— x sh— y_n ; д x n   2    2 n 2 ⁿ

д xn _ д Уп _ I     Y + ctg а дX дY а X12 +(Y + ctgа)2 ,

^д x n _ ^д У п _  ¹

X

—

—

д Y д X а X 1 ² + ( Y + ctg a ) ²

. (25)

РАСЧЕТ ТРАЕКТОРИЙ ЗАРЯЖЕННЫХ ЧАСТИЦ

расчетах полагалось, что Ф 0 _ V 0 _ 1. Из формулы (29) видно, что зависимость времени пролета от массы частиц определяется множителем у] 1 + ym , поэтому достаточно найти время пролета для случая y m _ 0. Начальные условия для траекторий при интегрировании уравнений (26), (27) на входе в зеркало задавались на оси у : х 0 , у 0 , у 0 , х 0 _ 71 — у о 2 . Время пролета определялось путем интегрирования дифференциального уравнения, получающегося из (29),

Будем считать, что электрическое поле корпускулярно-оптической системы в базовой декартовой системе координат х , у описывается двумерным электростатическим потенциалом Ф = ^ Ф ( х , у ) . При этом для производных потенциала также можно найти аналитические выражения.

Для расчета траекторий заряженных частиц можно воспользоваться теорией, изложенной в работе [4]. Траектории пучка в базовой системе

d r _      1

^d s    2 ( Ф + е )

Рассматривалось движение заряженных частиц в зеркале, для которого его собственная система координат X , Y связана с базовой соотношениями:

координат х , у описываются следующими ференциальными уравнениями:

диф-

Х _ — ( х — L х ) sin у + ( У — L у ) cos Y ,    (31)

Y _ — ( х — L_х ) cos у — ( у — L_v ) sin у .     (32)

x"

Φ x

x'

2 ( Ф + еФ 0 )   2 ( Ф + еФ 0 )

( x ^{ф +} У Ф ) ,

У " =

Φ y

y У

2 ( Ф + еФ 0 )   2 ( Ф + еФ 0 )

( x'фх + У ,фу ) .

В уравнениях (26) и (27) штрихи обозначают

Здесь L_x и L_y — расстояния, определяющие координаты средины основания зеркала, они задают положение зеркала; γ — угол, определяющий наклон оси Y зеркала к оси х базовой системы.

При расчете траекторий заряженных частиц точность вычислений должна быть очень высокой, особенно в тех случаях, когда речь идет о высоких

разрешениях приборов. Подчас для этого необходимо вычислять траектории заряженных частиц с относительной точностью до 10 ⁹ и выше. Для обеспечения такой высокой точности мы использовали аналитические выражения для потенциала и его производных, приведенные выше, а дифференциальные уравнения траектории (26), (27) интегрировали численно с помощью программы, реализующей четырехточечный метод Адамса с автоматическим выбором шага. Разгонные точки находились методом последовательных сближений Крылова. Относительная точность интегрирования выбиралась равной 10 - 8 ^ 10 " ⁹. Интегрирование велось по длине осевой траектории от s = 0

до S = S_k .

Для контроля точности вычислений тем же методом интегрировали также уравнения движения Ньютона. Эти уравнения в безразмерных переменных имеют очень простой вид [5]:

х = Ф х ,                      (33)

у = Ф у .                     (34)

Здесь точки обозначают производные по безразмерному времени т = t/т ₀ , где

х - х1 = У - У1

х ‘

У ’

входит в детектор в точке

k d х ck

Xd =

^- к 1 х 1 + ^У 1 ^-

yd = к1 (xd -

где

τ ₀

= 1 0

Am ₀

.

V 0 Zq e

В последней формуле А — массовое число, m ₀ — атомная единица массы, Z — зарядовое число, q_e — элементарный заряд. Во всех случаях для согласования результатов определялось время прилета частиц в детектор. Считалось, что плоскость детектора перпендикулярна осевой траектории пучка.

Для вычисления времени прилета произвольной частицы в детектор использовалась следующая процедура. Если осевая траектория выходит под углом к оси 0 х и попадает в детектор в точке ( x_ck , y_ck ), то прямолинейный участок осевой траектории описывается уравнением

хс ^{- Х}ск = У с ^- У ск х^С к            У*С к

Плоскость детектора перпендикулярна осевой траектории. Уравнение перпендикулярной прямой, соответствующей положению детектора, будет

( х - x ck ) х Ск = - ( у ^- у_С к ) у ’ к .         ⁽³⁷⁾

Траектория произвольной частицы, которая на выходе описывается уравнением

kd

—

k ₁

yck

,

^х 1 ) + У 1 ,

kd =

—

—

kck

хк У ’ к

.

Затем вычисляется расстояние от точки ( х ₁ , у ₁ )

до детектора s_d 1 = ^"(х а

—

х ₁ )² + ( y_d - У 1 ) 2 и вычис-

ляется время прилета частицы к детектору

t d = t 1 ±

s d 1

4 2(1 + £ ) .

Знак в (41) выбирается следующим образом. Сначала вычисляется величина

, _ У1 - Уск к1 с = х1 - xck

.

Если у ₁ >  У_ск , то знак "+" берется в том случае, если к _{1 с} > 0, или к _{1 с} <  k_d , иначе берется знак "-". Если у ₁ <  у_ск , то все наоборот.

Приведем результаты расчета времени прилета частиц в детектор, полученные путем интегрирования уравнений (26), (27) и (30), а также уравнений Ньютона (33), (34). Эти результаты можно рассматривать как тестирование созданной нами программы численного интегрирования системы дифференциальных уравнений.

Рассматривалось зеркало, поле которого рассчитано выше со следующими параметрами: а =- 2 ° , L₁ = 0.838, L ₂ = 0.954, L ₃ = 1.370, V 0 = 1, V = 0.8, V 2 = 0.4, V 3 = 0, V ₄ =- 0.0485. Все размеры и потенциалы даны в относительных единицах. Длина замыкающего электрода с потенциалом V ₄ = - 0.0485 равна 2 ед. Для осевой траектории задавались следующие начальные условия х ₀ = 0 , у_{с 0} = 3.275, у к ₀ = 0, х ‘ ₀ = 1. Конечная точка интегрирования для уравнений (1), (2) и (5) s_k = 30.18, при этом относительное время прилета осевой траектории в детектор т_к = 25.851767306. Для крайних траекторий пучка рассчитывалось время полета до плоскости детектора, перпендикулярной осевой траектории в конечной точке интегрирования. Относительная точность расчетов выбиралась

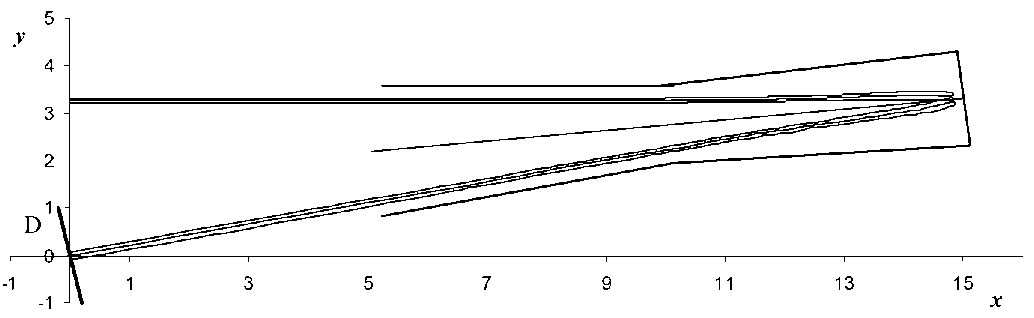
Рис. 4. Осевая и две крайние траектории пучка в зеркале (ширина пучка 0.1)

Результаты расчета времени прилета частиц

у0 τk Атк Интегрируемые уравнения 3.275 (осевая) 25.851767306 0 Траектории 3.325 25.854861757 0.003094451 Траектории 3.325 25.854861759 0.003094449 Ньютона 3.225 25.855485837 0.003718531 Траектории 3.225 25.855485843 0.003718533 Ньютона равной 10-9. Расчеты велись для пучка с относительной шириной 0,1. Рассматривались две крайние траектории параллельного пучка, для которых у0 = 3.325 и у0 = 3.225.

На рис. 4 представлены V-образная осевая траектория и две крайние траектории рассматриваемого пучка, черная линия, определяющая плоскость детектора, обозначена буквой D. Результаты расчета приведены в таблице.

Из результатов таблицы видно, что приведенные данные по времени прилета частиц τ_k совпадают до десятого знака. Это значит, что обе математические модели и программа численного интегрирования системы дифференциальных уравнений методом Адамса работают достаточно хорошо. В дальнейшем мы отдаем предпочтение уравнениям Ньютона (33), (34), т. к. они проще, не содержат особенностей и могут быть использованы при расчете систем с прямолинейной осью.

РАСЧЕТ ПОВЕДЕНИЯ ПУЧКОВ И ПРИБОРНЫХ ХАРАКТЕРИСТИК ВПМС

Рассматривалось поведение пучка заряженных частиц в ВПМС на основе предложенного пяти- электродного конического зеркала с V-образной осевой траекторией. Для нахождения траекторий интегрировались уравнения Ньютона (33), (34). Начальные условия для частиц пучка задавались Методом Монте-Карло в плоскости х0 = 0 . Координата у0 равномерно распределялась в области [Ус0 -Ау, ус0 + Ау], начальная скорость х0 — в области [ д/ 2 (1 - Em )-У2 , ^2 (1 + Em )- У2 ] , начальная скорость у0 изменялась от -0.001 до 0.001. Здесь 2 А у — ширина пучка, 2 Em — максимальный разброс по энергии в пучке.

Находилось время прилета в детектор каждой из N = 1000 частиц пучка, затем вычислялась разница между их временем прилета и временем прилета осевой частицы и строилось распределение частиц в зависимости от этой разницы во времени прилета. На рис. 5 приведен временной масс-спектр (распределение частиц по времени прилета в детектор) для двух масс, отличающихся на Y_m = 1/20 000 при нулевой начальной длительности импульса. Максимальный энергетический разброс в пучке 4 %. Ширина пучка 2 А у = 0.1, при ли-

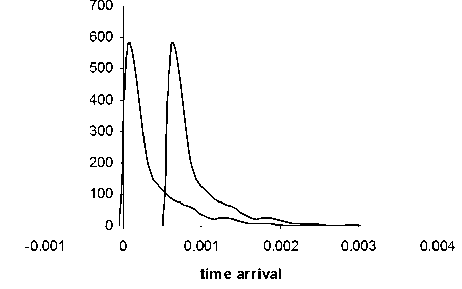
Рис. 5. Временной спектр для двух масс, отличающихся на y m = 120000, при нулевой начальной длительности импульса

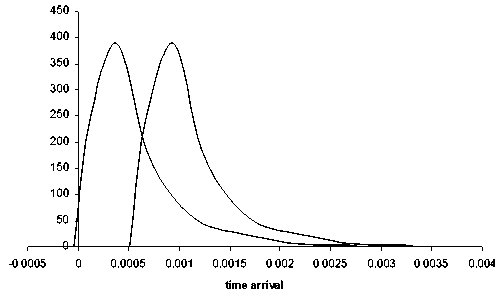
Рис. 6. Временной спектр для двух масс, отличающихся на y m = 120000, при начальной длительности импульса A tj т ₀ = 0.000491

нейных размерах замыкающего электрода 8 см (единичная длина 1 ₀ = 4 см) ширина пучка равна 4 мм.

Если энергия ионов на входе 4 кэВ, то для массы А = 1000 а.е.м. ( Z = 1) при начальной длительности импульса A t,. = 1нс ( A t , / т ₀ = 0.000491) для тех же масс получается масс-спектр, приведенный на рис. 6. Из рисунка видно, что разрешение 20 000 достигается примерно на полувысоте пика.

ной осью, в которых скорость частицы обращается в нуль в точке остановки. Анализ поведения пучков в ВПМС проведен путем интегрирования большого количества траекторий, начальные условия для которых находились методом Монте-Карло. Предложенный метод позволяет учитывать распределение частиц в источнике по координатам, и времени вылета, и по скоростям, а также свойства детектора и строить временные приборные спектры.