Расчет прочности элемента железобетонной балки

Величина предельного момента в элементе балки согласно рекомендациям «Строительных норм и правил» определяется по формулам, построенным при прямоугольной эпюре напряжений в сжатой зоне бетона. Эта модель, ориентированная на «ручной счёт», связана с искажением эпюры напряжений в бетоне и усилий в арматуре. Кроме того, упомянутые документы не содержат рекомендаций о рациональном отношении количеств растянутой и сжатой арматуры.

При нелинейном расчёте (НДМ) возможно найти оптимум этого соотношения, что, как правило, приводит к уменьшению количества арматуры в целом.

Принята комбинированная диаграмма деформирования бетона, показанная на рисунке. Она состоит из двух участков.

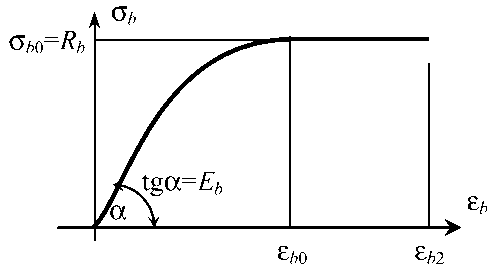
Кривая деформирования бетона

На криволинейном участке (0 < £ _b < £ _{b 0}) напряжения в бетоне определяются по формуле (1), рекомендованной Европейским комитетом по бетону (ЕКБ) [1].

На прямолинейном участке ( £ _{b о} < £ _b < £ _{b 2}) о b = R b .

. Г Л2

к £ b ( £ b |

к1 I

£ ь о V £b о J п/1 \

° b =---------—Rb ,

• 1    + ( к - 2 y^b- ^£ b о

Eb        Rb где к = —; Ebо = ; Eb = I 3— I; £ b - теку-Eb о         £ bo        V d £ b J щая деформация, £bо - деформация, при которой ° = Rb .

Напряжения в арматуре определяются по диаграмме Прандтля с параметрами £ s _о, £ s ₂, R s , зависящими от класса арматуры.

^о s =^£ s^Es при ^о <^£ s <^£ s о ;

° s = R s    при ^£ s о <^£ s <^£ s 2 -

Считается, что графики растяжения и сжатия и бетона, и арматуры подобны.

Задача ставится следующим образом. Заданы форма и размеры поперечного сечения элемента, характеристики бетона и арматуры: прочностные Rb и Rs и деформационные Eb и Es . Требуется определить количество растянутой и сжатой арматуры, обеспечивающей прочность элемента при заданном моменте М.

Для решения задачи составлены уравнения, алгоритм и программа АРМ подбора продольной арматуры балочных элементов.

Алгоритм подбора арматуры

Организуется итерационный ( k – номер итерации) процесс, в котором определяются следующие величины:

• 1.1.    Положение центра жесткости

zc , k - 1 ^_

_ ^ A bj E bj , k - 1 z bj ⁺ ^ A s , k - 1 E s , k - 1 z s ⁺ ^ A s , k - 1 E s , k - 1 z s ^ A bj E bj , k - 1 ⁺ ^ A s , k - 1 E s , k - 1 ⁺ ^ A s , k - 1 E s , k - 1

где величины, имеющие индексы ( k – 1), есть предыдущие, в частности начальные, их значения.

• 1.2.    Жёсткость элемента

B k ^_ ^ A bj E bj , k - 1 ( z bj ^- z c , k - 1 ) ⁺

⁺ ^ A s , k - 1 E s , k - 1 ( z s , k - 1 ^- z c , k - 1 ) ⁺

⁺zL A s , k - 1 E s , k - 1 ( z s ^- z c , k - 1 ) 2 .

• 1.3.    Кривизна элемента

w k _ MB .

• 1.4.    Деформации элемента

^e bj , k ^{_ (} z bj z c , k ) w k , ^e s , k ^{_ (} z s ^- z c , k ) w k , e': , k ^_ ( z s ^- z c , k ) w k .

• 1.5.    Напряжения в слоях бетона о bj , _k и в арматуре о _s , _k , o sk определяются по формулам (1) и (2).

• 1.6.    Секущие модули слоев бетона и арматуры по формулам:

° bj , k           ° s , k уч г    ° k

E bj , k ^_----- , E s , k ^_---- , E sk ^_ — .

,  ,,

• ^e bj , k             ^e s , k             ^e k

• 2.1.    Если деформация растянутой арматуры больше 2 e _{s 0} или эта деформация меньше 2 e _{s 0} , то

• 2.2.    Если абсолютная величина деформации в сжатом бетоне больше ε b 2 или меньше ε b 2 , то

Операции 1.1–1.6 выполняются до тех пор, пока z _c,k не будет отличаться от z _c,k–1 на достаточно малую величину.

На следующем этапе определяется необходимое количество растянутой и сжатой арматуры. Обычно деформации растянутой арматуры не превышают величины 2 e _s 0 _ 0,0035, что было учтено при разработке алгоритма.

.        .        e_s - 2e ₀ q

A к _ Ask -i + —---- s ° A 0.

^s , ^{k        s} , ^{k 1}         '*)_o

^{2 e} s 0

• + ^e b ^{2 e} b 2 /I⁰

• 2.3.    Возвращение к операции 1.1.

A s , k ^_ A s , k - 1 ⁺            A .

^{,          ,              e} b 2

В этих формулах A ⁰ _ 1 см².

Выполнение операций 1.1–2.2 продолжается пока разности A s , _k - A s , _k _ 1 и A s , _k - A s , _k _ 1 не станут достаточно малыми.

Корректировка арматуры. Если деформации в растянутой арматуре и бетоне имеют запас, то площадь растянутой арматуры можно уменьшить:

A (2) _ A (1)        .

^e s 0

Итерационный процесс заканчивается, когда площадь арматуры ( n + 1)-й итерации будет отличаться от площади n -й итерации не более чем на приемлемо малую величину.

Этот алгоритм позволяет выполнять и поверочный расчет, в этом случае пункты 1.6 и 2.1–2.3 не выполняются.

Этот алгоритм позволяет выполнять как поверочный расчет, так и подбор арматуры.

Во втором случае пункты 2.1–2.3 не выполняются.

Примеры расчётов

Рассмотрены четыре примера, заимствованные из пособия [2], где приведены исходные данные и решения, полученные по известным формулам СП [3]. Эти же примеры решены нами по НДМ с помощью описанного выше алгоритма. Номера примеров такие же, как приняты в [2]. Результаты расчётов сведены в таблицу.

В примерах 4, 6 и 8 сечение разбивалось на 10 слоёв, в примере 7 – на 16, поскольку центр жесткости сечения в этом случае оказался близким к границе примыкания полки к стенке и добиться устойчивого решения при меньшем числе слоёв не удалось.

Во второй строке таблицы приведены исходные данные поперечных сечений и изгибающие моменты, на действие которых производился расчёт.

В третьей строке показаны рисунки, на которых даны обозначения, принятые в расчётах.

Цифры четвертой строки обозначают колонки с результатами расчётов:

• 1    – по формулам СП [3], 2 – по программе АРМ.

Во второй снизу строке таблицы приводятся значения напряжений ° b в слоях бетона. Во всех случаях они вычислены по программе АРМ. Но в колонках, обозначенных цифрой 1, показаны результаты, полученные при арматуре, принятой в пособии [2].

В тех слоях, где напряжений нет, стоят нули – там прошли трещины.

В последней строке таблицы показаны значения растягивающих и сжимающих напряжений в арматуре.

Теория инженерных сооружений

Сопоставление результатов расчетов балочных элементов

	Пример 4		Пример 6		Пример 7		Пример 8
	Определить площадь сечения продольной арматуры: M = 7.8-106 кг-см, b = 30 см, h = 80 см, a = 5 см, a * = 3 см, Rs = R sc = 3550 кг/см2, Rbn = 85 кг/см2		Проверить прочность сечения: M = 6.367-106 кг-см, b = 30 см, h = 70 см, A s = 37,32 см2, A' s = 4,82 см2, а = 7 см, а' = 3 см, Rs = R sc = 3550 кг/см2, Rbn = 115 кг/см2		Определить площадь сечения продольной арматуры: M = 2.6-106 кг-см, b f = 150 см, h f = 5 см, b = 20 см, h = 40 см, а = 8 см, Rs = R sc = 3550 кг/см2, Rbn = 145 кг/см2		Определить площадь сечения растянутой арматуры: M = 2.7-106 кг-см, b f = 40 см, h f = 12 см, b = 20 см, h = 60 см, а = 8 см, Rs = R sc = 3550 кг/см2, Rbn = 85 кг/см2
	_L             ____ jv '$				-I—^ .-^^^^         — — я„1; уут/тЖ^ А s J^^^ _L       ______ ■ к          46
	1	2	1	2	1	2	1	2
A s , A' s (см2)	37.24,8.63	39.59,6.87	37.32,4.82	40.22,2.81	24.46,0	24.43,0	19.49,0	17.89,0
£ b / е b 2	- 0.80	- 1.01	- 0.8623	- 1.00	- 0.56	- 0.57	- 0.55	- 0.58
е s / е s 0 , £ ' s / £ s 0	1.02, - 2.03	1.02, - 2.03	1.16, - 1.73	1.00, - 2.00	9.23	0.93	0.91	1.00
σ b по слоям* (кг/см2)	0,0,0,0, - 21, - 69, - 81, - 84, - 85, - 85	0,0,0,0, - 64, - 80, - 84, - 85, - 85, - 85	0,0,0,0, - 11, - 88, - 109, - 114, - 115, - 115	0,0,0,0, - 70, - 104, - 113 - 115, - 115, - 115	0,0,0,0,0,0,0,0, 0,0,0,0, - 0, - 0, - 88, - 145	0,0,0,0,0,0,0,0, 0,0,0,0,0,0, - 88, - 145	0,0,0,0,0, 44,70,80, 83,85	0,0,0,0,0, 41,70,80, 84,85
о s , a ' s (г/см2)	3550, - 3550	3550, - 3550	3550, - 3550	3550, - 3550	3550	3373	3264	3550

*Результаты расчётов в колонках: 1 - по СП [3], 2 - по НДМ (программе АРМ).

85		16569	115		16578
85			115
85 с		115869	115 с		115934
84	V		113	V
80	1,		104
64	1—	132438	7С <		132512

Количество растянутой арматуры A s в прямоугольных сечениях по АРМ получается больше, чем по [2], а количество сжатой арматуры A s по АРМ меньше, чем по [2]. В суммарном выражении расход арматуры по нелинейному расчёту (АРМ) во всех примерах оказался примерно на 6 % меньше, чем по [2].

На иллюстрациях показаны эпюры напряжений в бетоне, а также суммы напряжений, действующих: в бетоне - средняя стрелка; в растянутой арматуре - нижняя стрелка и сжатой арматуре -верхняя стрелка. Левый рисунок составлен по решению четвертого примера. На правом показаны результаты решения шестого примера. В обоих случаях данные получены по программе АРМ.

Заключение

• 1.    Составлены алгоритм и программа АРМ, позволяющие выполнять нелинейные расчёты железобетонных балочных элементов.

• 2.    Нелинейные расчёты дают возможность определить потребное количество растянутой и сжатой арматуры, напряжения и деформации в бетоне и арматуре, определить область сечения, охваченную трещинами.

• 3.    Результаты расчётов арматуры по формулам СП [3] и по нелинейной деформационной модели (программа АРМ) являются близкими.

• 4.    Существует множество соотношений площадей растянутой и сжатой арматуры, при которых прочность сечения обеспечена. Следовательно, есть возможность найти такое соотношение, при котором расход арматуры минимален.