Расчет продолжительности оптимального по времени разворота космического аппарата при смене режимов ориентации
Автор: Алиев-Хетагов Рашид Саядуллаевич
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 5 (45), 2012 года.
Бесплатный доступ
Рассматривается угловое движение автоматического космического аппарата (КА), каждый виток которого состоит из двух участков: рабочего (в окрестности апогея), на котором КА решает целевую задачу, и дежурного, на котором выполняется коррекция орбиты с использованием электрореактивных двигателей и инерционных исполнительных органов, - маховиков. При этом для перехода в режимы коррекции орбиты или ориентации на рабочем участке совершаются программные развороты космического аппарата. С помощью математического моделирования проведено сравнение двух способов разворота КА, оптимальных по быстродействию, при различных начальных данных.
Оптимальные по времени угловые развороты
Короткий адрес: https://sciup.org/148176935
IDR: 148176935 | УДК: 531.38
Calculation of time-optimal maneuvers of a spacecraft in case of changing modes of orientation
The author considers angular movement of a space vehicle. The spiro consists of two phases: workable control (in an apogee vicinity) during which the device is to solve a target problem, and duty control phase During duty control phase of the orbit the problems of orbit correction performance are solved with the help of electrojet engines and gravitational unload of accumulated angular momentum of operating members, namely, flywheels. At the process, for transition to orbit correction modes or for transition into demanded orientation on workable control phase, program maneuvers of a space vehicle are made. From the point of view of increase in time taken for gravitational unload is expedient to minimize durations of maneuvers of a space vehicle. Comparison of two ways of maneuvers of a space vehicle, optimum on speed [1, 2], is made. Comparison is made by the results of mathematical modeling at various sets of initial data.
Текст научной статьи Расчет продолжительности оптимального по времени разворота космического аппарата при смене режимов ориентации
Рассмотрим систему инерционных исполнительных органов (ИИО), состоящую из четырех маховиков, оси вращения которых перпендикулярны разным граням правильного многогранника – тетраэдра. Область вариации кинетического момента системы ИИО в первом приближении представляет собой шар радиусом R = 1,633 h , где h - модуль вектора кинетического момента одного маховика при его максимальной скорости вращения.
Будем использовать инерциальную систему координат. Кинематические уравнения зададим в кватернионной форме.
Развороты космического аппарата выполняются двумя способами.
Первый способ – плоский разворот вокруг вектора конечного поворота с максимальной угловой скоростью (рис. 1) [1; 2].
Обозначим суммарный вектор накопленного кинетического момента космического аппарата и инерционных исполнительных органов через G 0 и будем считать, что за время разворота приращением вектора G 0 за счет действия моментов внешних сил можно пренебречь. Тогда вектор G 0 остается неизменным в инерциальной системе координат.
Из кватерниона рассогласования положения космического аппарата найдем мгновенную ось разворо- та, относительно которой будем совершать плоский разворот в пространстве [3]:
* *
e = e ( e l , e 2 , e 3).
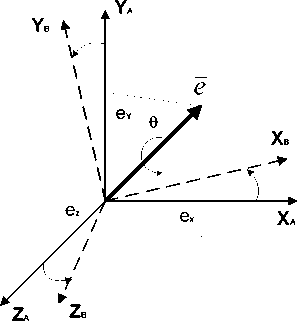
Рис. 1. Эйлерова ось вращения, определяющая поворот системы координат:
OXAYAZA – инерциальная система координат; OXBYBZB – связанная система координат
Обозначим угловую скорость вокруг вектора конечного поворота через ю . Тогда G0 = H + ® Je , где
Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева
H – суммарный кинетический момент инерционных исполнительных органов; J – тензор моментов инерции космического аппарата [4]. При развороте с максимальной угловой скоростью модуль вектора H равен R . В этом случае R 2 = ( G0 - ω Je )2, откуда получим уравнение [2]:
( Gje) ± V ( G j e )2 - ( j e ) 2 ( g 02 - r 2 ) to =-------------------e^----------------- .
( Je )2
Второй способ – пространственный разворот с максимальной текущей проекцией угловой скорости на вектор конечного разворота [3] (рис. 2). В данном способе угловая скорость разворота находится минимизацией функции I = ( e · ω ) при условии | H | = R . Решая задачу методом множителей Лагранжа, определим компоненты вектора H ( H 1 H 2 H 3):
H i
R ei Ji
2 ei i=1,2,3,
а также найдем угловую скорость разворота
1 - _
B = - (e • B .
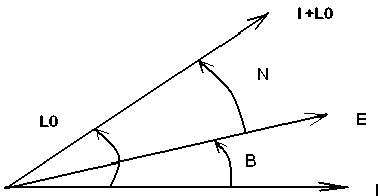
Рис. 2. Связь между связанной E и инерциальной I системой координат с учетом кватерниона разворота L 0
Приведем результаты математического моделирования для двух способов разворота, который проводился по 26 различным направлениям с углом разворота 180°.
Анализ полученных результатов показывает, что в 34 случаях предпочтительнее первый способ, в 44 случаях – второй способ.
|
№ направления |
Кватернион разворота |
Суммарный кинетический момент Т (0; 0; 0), с |
Суммарный кинетический момент Т (5; 5; 5), с |
Суммарный кинетический момент Т (10; 10; 10), с |
|||
|
Первый способ |
Второй способ |
Первый способ |
Второй способ |
Первый способ |
Второй способ |
||
|
1 |
+ X |
1 036,3 |
1 027,46 |
963,5 |
944,535 |
931,0 |
890,609 |
|
2 |
– X |
1 036,3 |
1 027,46 |
1 195,3 |
1 262,13 |
1 908, 9 |
1 859,25 |
|
3 |
+ Y |
1 231,9 |
1 238,35 |
1 145,2 |
1 137,89 |
1 098,7 |
1 093,46 |
|
4 |
– Y |
1 231,9 |
1 238,35 |
1 160,0 |
1 384,84 |
1 527,1 |
1 515,31 |
|
5 |
+ Z |
761,5 |
731,668 |
761,5 |
805,639 |
761,5 |
1 401,85 |
|
6 |
– Z |
761,5 |
731,668 |
761,5 |
702,012 |
870,3 |
1 127,96 |
|
7 |
+ X – Y |
1 147,2 |
1 165,32 |
1 187,9 |
1 120,48 |
1 357,7 |
1 057,38 |
|
8 |
– X – Y |
1 147,2 |
1 165,32 |
1 395,3 |
1 377,53 |
1 954,1 |
1 809,31 |
|
9 |
+ X + Y |
1 147,2 |
1 165,32 |
1 012,3 |
1 005,65 |
940,5 |
909,856 |
|
10 |
– X + Y |
1 147,2 |
1 165,32 |
1 185,4 |
1 321,87 |
1 350,1 |
1 747,75 |
|
11 |
+ X + Z |
861,7 |
922,506 |
837,9 |
827,09 |
837,9 |
761,422 |
|
12 |
+ X – Z |
861,7 |
922,506 |
903,7 |
1 078,5 |
1 039,3 |
1 450,94 |
|
13 |
– X – Z |
861,7 |
922,506 |
985,2 |
937,305 |
1 271,7 |
1 038,99 |
|
14 |
– X + Z |
861,7 |
922,506 |
908,5 |
1 114,28 |
1 053,6 |
1 510,18 |
|
15 |
+ Y + Z |
994,4 |
920,85 |
928,8 |
988,239 |
902,2 |
1 065,82 |
|
16 |
+ Y – Z |
994,4 |
920,85 |
979,0 |
972,079 |
1 051,6 |
1 217,22 |
|
17 |
– Y – Z |
994,4 |
920,85 |
1 234,5 |
1 138,89 |
1 773,2 |
1 666,87 |
|
18 |
– Y + Z |
994,4 |
920,85 |
987,3 |
891,888 |
1 074,0 |
888,403 |
|
19 |
+ X + Y + Z |
1 006,0 |
935,923 |
886,1 |
858,509 |
884,1 |
814,118 |
|
20 |
+ X + Y – Z |
1 006,0 |
1 032,43 |
962,9 |
1 075,11 |
962,4 |
1 180,48 |
|
21 |
+ X – Y – Z |
1 006,0 |
928,423 |
1 142,7 |
1 152,8 |
1 472,2 |
1 684,21 |
|
22 |
+ X – Y + Z |
1 006,0 |
1 048,84 |
955,1 |
923,625 |
942,4 |
860,592 |
|
23 |
– X + Y + Z |
1 006,0 |
1 048,84 |
1 017,6 |
1 186,25 |
1 105,3 |
1 518,59 |
|
24 |
– X + Y – Z |
1 006,0 |
928,423 |
1 062,6 |
958,757 |
1 201,8 |
1 283,0 |
|
25 |
– X – Y – Z |
1 006,0 |
1 032,43 |
1 261,0 |
1 195,24 |
1 853,5 |
1 556,59 |
|
26 |
– X – Y + Z |
1 006,0 |
935,923 |
1 088,1 |
999,991 |
1 281,8 |
1 177,34 |
Вместе с тем можно отметить, что в большинстве случаев времена разворота приблизительно одинаковы и отличаются, как правило, на 5…10 %. А если учесть, что первый способ характеризуется большей простотой вычислений, а следовательно меньшими затратами используемых ресурсов бортовой ЦВМ, то именно он может считаться более оптимальным.
Таким образом, по результатам сравнения двух способов разворота КА за минимальное время выбран оптимальный способ разворота для бортовой ЦВМ.
