Расчет продолжительности процесса термовлажностной обработки полуфабрикатов на основе животного и растительного сырья

Цель работы – исследовать влияние технологических режимов на процессы тепло- и массообмена при тепловой обработке изделий, обосновать ресурсосберегающие режимы тепловой и низкотемпературной обработки полуфабрикатов и готовых изделий на основе рыбно-печеночнорастительных композиций.

Расчет параметров термообработки исследуемых систем (продолжительность процесса, распределение температуры внутри изделия и изменение его массы) осложнен как внешним, так и внутренним переносом влаги. В связи с этим строгое математическое описание влаго-и теплообмена между поверхностью полуфабриката, который необходимо рассматривать как капиллярно-пористое тело, и окружающей средой должно основываться на совместном решении уравнений гидродинамики и конвективного тепло- и массопереноса с учетом нормальной составляющей массового потока на поверхности тела, что усложняет задачу [1–4]. Тем не менее, рассмотрение такой задачи в части, касающейся переноса влаги под действием градиентов влагосодержания, температуры и давления возможно, если движущими силами процессов переноса считать не эти градиенты потенциалов на поверхности капиллярнопористого тела, а разности между потенциалами, усредненными по поверхности и объему тела.

Успешное применение этой теории для широкого использования при решении практических задач осложняется отсутствием систематизированной базы данных по гигро- и гидроскопическому равновесию обрабатываемых полуфабрикатов с технологическими средами. С другой стороны, даже при наличии экспериментальных данных по гидро- и гигроскопическому равновесию в этом случае находятся не поля потенциалов переноса, а только их среднеобъемные и среднеповерхностные значения, что принципиально не позволяет рассчитать длительность термообработки как время достижения необходимой температуры в центре продукта [5, 6].

Результаты и обсуждение

Мясные и рыбные продукты обрабатываются при не слишком высоких температурах и вследствие этого градиенты потенциалов переноса внутри капиллярнопористых тел не слишком велики, поэтому можно считать, что внутренний перенос влаги существенно не изменяет температурное поле внутри мясных и рыбных изделий. В связи с этим, для определения времени достижения кулинарной готовности полуфабрикатов целесообразно рассматривать не сопряженную систему уравнений переноса количества движения, теплоты и массы, а только нестационарное уравнение теплопроводности, которое в декартовой системе координат имеет вид:

6 t ( 6² 1 62 1 62 1 — — a I —7 + 7 +—7 6т    (6 x² 6 y 6 z²

где τ – время, с; а – температуропроводность продукта, м /с; t – температура,°C.

Решая уравнение (1) с соответствующими начальными и граничными условиями можно найти распределение температуры от времени в теле произвольной формы, причем в общем случае это возможно лишь использованием численных методов.

Для тел простейшей формы (неограниченные пластина и цилиндр, шар) уравнение (1) становится одномерным

6 1      1 6 ( n 6 1 )

— — a --1 x — I , 6т     x n 6 x ( 6 x )

где n – индекс формы (0 – пластина; 1 – цилиндр; 2 – шар) и может быть решено аналитически.

В [3, 4] предполагается, что температурные возмущения в обрабатываемом изделии распространяются с конечной скоростью, что характерно для мясных и рыбных продуктов, а производная по времени в уравнении (2) для области, где за счет взаимодействия с окружающей средой происходит изменение температуры, заменяется ее средним значением по переменной во времени подлине возмущенной области. При этом уравнение (2) превращается в обыкновенное дифференциальное уравнение, для которого ищется решение задачи распространения теплоты в исследуемых системах.

Замена производной в уравнении (2) ухудшает точность описания температурного поля внутри изделий. Кроме того, следует отметить, что при термической обработке пищевых полуфабрикатов сложно учитывать происходящие при этом различные физико-химические превращения (тепловая денатурация белковых веществ, разваривание и дезагрегация коллагена, изменение состояния и свойств жиров, разваривание и клейстеризация крахмалов, изменение структурно-механических свойств), которые вызывают изменение теплофизических характеристик объектов исследования. Если учесть, что справочные данные по их температурным зависимостям весьма ограничены [6, 7], а уравнения конвективного теплопереноса обычно позволяют определить характеристики теплообмена между телом и окружающей средой с точностью порядка 20% [1, 2, 9], использование классического уравнения нестационарной теплопроводности (2), в котором скорость распространения теплоты предполагается бесконечно большой, для расчета продолжительности термообработки рыбно-печеночно-растительных полуфабрикатов можно считать достаточно обоснованным. Как показывает практика инженерных расчетов аналитические зависимости из [3, 6, 8], выведенные для различных начальных и граничных условий, позволяют получить результаты, вполне согласующиеся с вычислениями времени достижения кулинарной готовности продуктов по формулам из [4, 5]. К тому же геометрия подвергаемых термообработке изделий, в которых можно аналитически определить распределение температуры, в данном случае может быть расширена за счет того, что кроме тел в виде неограниченных цилиндра, пластины и шара, можно рассматривать тела конечных размеров, получающиеся при пересечении приведенных выше тел простейшей формы.

С учетом сказанного рассчитаем время достижения кулинарной готовности, то есть достижения температуры 80 °Cв центре изделий, при их термообработке в печи с вынужденной конвекцией и увлажнением теплоносителя. Будем рассматривать биточки как тело в виде ограниченного цилиндра, получающегося при пересечении неограниченного цилиндра диаметром 2R и неограниченной пластины высотой 2h .

Для выбора расчетной формулы необходимо обосновать вид граничных условий. В связи с этим необходимо учесть, что после разогрева и подачи воды в рабочей камере аппарата образуется содержащая водяной пар и аэрозольные частицы воды среда, при взаимодействии которой с обрабатываемым изделием происходит интенсивный теплообмен, сопровождающийся конденсацией пара и осаждением аэрозольных частиц на поверхности изделий. В этом случае коэффициенты теплоотдачи между изделием и окружающей средой достаточно велики и, следовательно, можно предположить, что на поверхности биточков реализуются граничные условия первого рода, то есть температура поверхности изделия совпадает с температурой окружающей среды ^{t c} . Кроме того, будем считать, что начальная температура изделия одинакова по всему его объему и равна ^{t 0} . Нахождение температурного поля тела в виде цилиндра конечных размеров связано с решением дифференциального уравнения теплопроводности:

дt ( r, z ,t ) —----= a дт д 21 ( r, z ,t ) + д r 2

1 д 1 ( r , z , т )    д ² 1 ( r , z , т )

r    д r          дz²

,

( т >  0; 0 <  r <  R ; - h <  z < + h )

при начальном условии

1 ( r, z ,0) = 10 = const и при граничных условиях

1 ( r , ± h , t ) = 1 c ; 1 ( R , z , t ) = 1_C

Решение сформулированной в безразмерном виде О ( r , z , т ) таково:

О ( r , z , т ) = О ( r , т ) • О ( z , т ) ,

задачи

где О(r,т) = ( 1c -1 (r,t))/(1c -10) - решение для неограниченного цилиндра, а О(z,т) = ( 1C -1 (z,t))/(1C -10)-      решение для неограниченной пластины, пересечением которой с неограниченным цилиндром образован конечный цилиндр. В этом случае начальные и граничные условия остаются прежними, то есть 1 (r ,0) = 1 (z ,0 ) = 10 = cons1,       (7)

1 ( R , t ) = 1 ( ± h , t ) = 1_c = cons1, (8)

а решение поставленной задачи определяется выражением:

\ 1= - 1 ( r , z , t )

0 ( r , z , t ) =  ----------^L =

4 ^{- 1} 0

Г r i ( z 1

= ZZ A n A m J 0 I А ,— I cos I M m - I x n = 1 m = 1           V    ^R )    V     h )

X exP I

M n

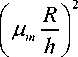
Fo ^ ,

где An m J ( m ), Mn — корни характеристического уравнения J0 (Mn ) = 0, J0 (Mn) и J1(Mn) -функции Бесселя первого рода нулевого и пер-Am =(-1) m+1 — вого порядка соответственно,            Mm , n ” Fo = —

Mm =^{( 2} m - 1) Fo R 1 .

,

.

При этом среднюю температуру биточков, необходимую для определения их теплофизических характеристик, можно найти по формуле to to ой =ZZBnBm • exp

—

2 , Г ^R 1 ^M n ⁺ I ^Mm— I

V h )

^Fo f , (10)

B = A где n M n ² ,

Bm = ^^

Mm •

Переход от безразмерной температуры к размерной осуществляется по выражению t ( r , z ,T ) = t c - в ( r , z,T ) ■ ( t c - t 0 ) . (11)

Результаты вычислений температуры в центре изделий и их средней температуры при разли чных условиях термообработки в конвектомате приведены в приложении и на рисунке 1, где для сравнения также представ лены результаты экспериментального исследования времени достижения кулинарной готовности рыбно-печеночно-растительных биточков. В этих опытах использовали изделия массой около 52 г., содержащие по 36,4% говяжьей печени и филе зубатки, 13% геркулеса 10% воды и 4,5% соли. В биточки (изделия приплюснуто-цилиндрической формы) диаметром около 6 см и высотой около 2 см с помощью специального приспособления вводили термокерн и затем помещали в разогретый пароконвек-томат с определенными температурой и подачей воды. После достижения заданного времени фиксировали температуру в центре продукта и вынимали его из конвектомата для контроля положения термокерна и массы изделия.

Как показывают результаты расчетов изменения температуры в центре рыбно-печеночнорастительных биточков, рассматриваемых как цилиндры конечных размеров, достаточно хорошо согласуются с экспериментальными данными.

Без подачи воды теплообмен между изделием и окружающей средой, имеющей постоянную температуру, осуществляется по конвективному механизму и можно считать, что на поверхности биточков будут реализовываться граничные условия третьего рода.

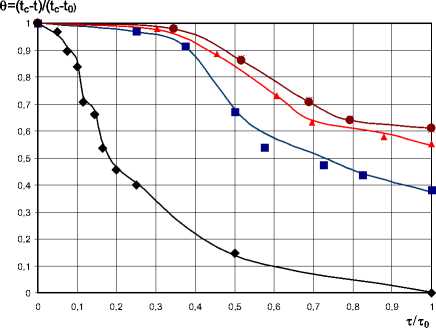
120 эксп       120 расч       160 эксп       160 расч

180 эксп       180 расч       80 эксп        80 расч

Рисунок 1. Изменение температуры в центре рыбнопеченочных биточков от времени

Figure 1. Change in temperature in the center of fishliver cells from time

Распределение температуры внутри цилиндра конечных размеров при условии симметричности задачи найдется из решения системы уравнений (3)–(4) и (12)–(15):

• -6-^ + a[tc -t(R,z,r)] =0,(12)

rT

^^ = 0; t ( 0,z,T ^, dt (r, h ,t )

• ■ -    tc ^- t ( r , h^{, T} ) ] = ⁰

dz      At,

5 t(r ,0,T)=0 dz’

где ^A - теплопроводность комбинированных рубленых систем, Вт/(м К); а – осредненный по поверхности коэффициент теплоотдачи цилиндрического тела конечных размеров, Вт/(м²∙К).

Начало координат находится в центре цилиндра.

Как и ранее решение сформулированной задачи в безразмерном виде определится уравнением (6). Начальные условия определяются уравнением (7), а граничные условия для не- ограниченных цилиндра и пластины остаются такими же, как и для цилиндра конечных размеров, то есть

-^+a[tc-t(R,t)]=0,(16)

-^+a[tc-t(h’T)]=0.(17)

at (0,7) at(0,T) = 0

a r       a z

Расчетное соотношение для нахождения поля температуры внутри ограниченного цилиндра имеет вид:

t_c - 1 ( r , Z , T )

y( r, Z ,T )= c------------ = tc - t0

( r If Z 1

= ZE AkAJ 0 I M k"^ I cos I M iT I x (19)

k = 1 l = 1           V ^R J V h 7

exp *

x

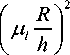
Fo ^ ,

A =      2 Bii где               k J0 (Mk)[M2 + Bii2] ,

A i = ( - 1 ) l ^{+ 1}

2 Bi ₂ Bi 22 + м 2

M l ( Bi 22 + Bi ₂ + M l ²)

Здесь F t и ^ ' - корни характеристиче- . ^J 0 ⁽ " ) ₌ ^в etg ^ =     B^ = ^ R

^СКиХ УРа^ВНеНий: J 1 _{( Ц к} ) Bi 1 ;         Bi 2 ;       Х _Т

а и Bi2 = x - числа Био для неограниченных

цилиндра и пластины соответственно.

Осредненный по поверхности биточков коэффициент теплоотдачи находится из соотношения:

Здесь M , = 18,016 кг/кмоль, M _sa = 28,96 кг/кмоль – молярные массы водяного пара и сухого воздуха соответственно; t = T/T _o; Т - температура рабочей среды в конвектомате, К; Т ₀ = 273,15 К; Х - влагосодержание паровоздушной смеси, которое находится через задан-

ную относительную влажность воздуха φ по формуле [4, 11]:

а =

а ₁ F ₁ + а ₂ F 2

F + F 2

x =

ф—

--------г— M ^ 4Й, (26)

( р!р. ) t^A exp [^{- B} ( ^{1 -} 1 - ) + С ( ¹ - t ) ]- ф

где а ₁ и а ₂ - коэффициенты теплоотдачи от боковой и торцовой поверхности цилиндра, площади которых равны соответственно F и F ₂.

Коэффициент теплоотдачи от торцовой поверхности цилиндра рассчитывается как для случая теплообмена при обтекании плоской поверхности длиной 2 R . Для Re <  ⁵ 40 5 расчетное соотношение имеет вид [4, 5]:

Nu₁ = 0,664 Re¹¹² Pr^1/3

_ а • 2 R Pr c^

где ^{NU 1} = ; X ; ^Re = u • ^{2 R} / v X, v, pe — теплопроводность Вт/(м К), кинематическая вязкость, м²/с, и объемная теплоемкость влажного воздуха, Дж/(м³ К); u - скорость обтекания биточков влажным воздухом, м/с.

Коэффициент теплоотдачи от боковой поверхности цилиндра для 10³ <  Re <  2 • 10⁵ определяется по формуле:

Nu ₂ = 0,25Re⁰¹⁶Pr⁰¹³⁸ , (22)

Численные значения коэффициентов А, В, С, согласно [4,5], равны A = 9,248 ; B = 27,098 ; С = 2,005 ; р = 101325 Па - давление в камере конвектомата, которое примем равным атмосферному давлению; ^р> = 610,8 Па -давление насыщенных паров воды при Т ₀ = 273,15 К.

Плотность влажного воздуха рассчитывается по зависимости из [7, 4]:

p = p , ( x + ¹ ) / ( x + ^M, I ^m fa ) ,    (27)

где плотность водяного пара ^р , можно найти из уравнения состояния

P i =

^Mi P RT

где

Nu ₂ =

a ₂ • 2 R X

Для влажного воздуха, который является бинарной смесью водяного пара и сухого воздуха, приближенное значение коэффициента

теплопроводности определяется по правилу аддитивности согласно [4, 10]:

X =

M

^Lfa ^MNA

M, x + ——

^M na

где теплопроводность водяного пара и сухого воздуха рассчитываются соответственно по следующим соотношениям:

^X 1

X ,

0,0595 • t °’⁵

1 + 2,46 t

0,0347 • t °'⁵ 1 + 0,454 t

,

.

R = 8314 Дж/(кмоль К) – универсальная газовая постоянная.

Объемная теплоемкость среды определяется по формуле из [5]:

p c = р ,^e, ( x + c _SA I n, ) / ( x + M I ^m fa ) , (29) где изобарные теплоемкости водяного пара и воздуха равны соответственно при 80 °C n , = 1873 Дж / (кг К), n_SA = 1006 Дж / (кг К), а при 120^о С п , = 1894 Дж / (кг К), n_SA = 1012 Дж/(кг К) [9].

Заключение

На основе исследований процессов тепло-и массообмена при тепловой обработке комбинированных рыбно-печеночно-растительных систем обоснованы ресурсосберегающие режимы термовлажностной обработки комбинированных изделий: обжаривание при t =200 °С, без увлажнения, продолжительность 5 мин; запекание при 180 °С, расход воды на увлажнение (4,0-4,3). 10-6 м3/с, продолжительность 10 – 15 минут, обеспечивающие снижение технологических потерь массы готового продукта с 18% до 5–7%.