Расчет пространственно-частотных характеристик дифракционного поля от секторных отверстий

Дифракция Френеля, являющаяся квадратичным приближением формулы Кирхгофа и подтверждаемая многочисленными экспериментами, является одной из классических задач [1]. Дифракционное поле в зоне Френеля сводится к интегралу по области отверстия с быстро меняющейся подынтегральной функцией. В зависимости от формы отверстия такие интегралы редко явно вычисляются; с другой стороны, при больших значениях фазового параметра прямые численные методы становятся здесь непригодными. В таких случаях обычно обращаются к их асимптотической оценке, которые имеют свои границы. Поиск аналитических решений для дифракции Френеля от областей различных конфигураций является актуальным. Несмотря на то, что дифракционная задача в постановке Френеля сложилась давно, ее аналитические решения были найдены сначала в случае отверстий двух конфигураций: прямоугольных и круглых [2, 3], а затем в случае секторного отверстия [4, 5].

Аналитические решения в области оптики необходимы для получения достоверного трехмерного распределения света вблизи фокальной точки, что имеет особое значение для оценки величины допуска в требуемом положении плоскости систем, формирующих изображение. В микроволновой части радиоволн они необходимы для анализа пространственной неоднородности структуры поля от различных дифракционных систем (ослабляющие экраны, сложный рельеф местности.

Для расчета пространственно-частотных характеристик дифракционного поля от секторных отверстий будем пользоваться решениями, полученными в [4, 5]. В этих работах были найдены аналитические выражения для множителя дифракционного ослабления Ф = W/W0, где W – дифракционное 2п поле от отверстия, а W = expi ^rr) / ro - поле прямой невозмущенной волны в точке наблюдения за отверстием на расстоянии ro от источника; λ – длина волны. Остальные параметры задачи приведены на рис. 1.

Искомая функция Ф найдена как сумма (луч проходит по отверстию) или разность (луч проходит вне отверстия) результатов интегрирования по двум смежным составляющим секторам, когда луч проходит по их общему прямому краю (рис. 1):

Ф(Р о , ф о ) = Ф(Р о , ф 1 ) ± Ф(Р о , Ф 2 ),

где i1

Ф ( р 0 , ф j ) = - —n n exp( i n n 0 ) J exp( i n nu

^ф j

Здесь приняты следующие обозначения: V n = R/ b ; ^ n o = p o / b - относительные величины радиусов сектора и точки прохождения луча, где b = ^X- z; и = p/ R – переменная интегрирования. Использованы полярные координаты р, ф с центром, совмещенным с центром секторного отверстия: x = р cosф, у = р sinф , Р о =Ах О + У о ² .

В работах [7, 8] для уравнения (2) получены следующие аналитические выражения: для области наблюдения q/p ≥ 1

^{Ф (} Р 0 , ф ) = ^- ^xP-L i ^ ^^+ n )] . [ V 0 - ⁽ ф , p ) - i V ₁ ^{- (} ф , p ) ^]- 2_F ^{( и} 3 ) . ^[ F ^{( и} — ) - F ( у ^ ^] .

+ exp (i n П о )

го

- Z ( - 1)

к - 0

k ^{(2 п n}0 ^)2k

A 2k

C 2k

го i z (-1)

k = 0

/ 3 _ i 2 k + 1 k (2 ^п n о ⁾

A 2k + 1

с l- 2 k + 1

и для области наблюдения q/p ≤ 1

^{ф (} Р о , ф ⁾ =

exp[i n ( n₀ + n)]

\ U₂(ф,p) + iU₁( ф ,p) ] +

exp(inn0) . x , xk

⁺     '   0 sin ф cos ф Х ⁽ - ^{1) G}k • ^J 2k - 1

²                    k - 1

где

G k = (iq)

k + 1 ^si n^2k ф

^Ak + 1

J k - J

i qu e2 u

2 k + 1 e - ipu cos ф du

Здесь по аналогии с задачей Ломмеля на круге [2] введены функции, имеющие внешнее сходство с функциями Ломмеля [6]:

V S ( ф . р ) =

2 k + S

^- E — - k + S ( ф , p ) ,

го

U S ( ф , p ) - z ( - 1

k - 0

2 k + S

- E 2 - k + S ( ф , p ) ,

где E _v ^- ( ф , p ) - неполные цилиндрические функции в форме Пуассона [7, 8], имеющие интегральное представление

_ .             2 p ^V ф

E ( ф , p ) - -----j exp ( - ip cos t ) sin A v 0

и представление в виде степенного ряда относительно переменной р v                          k

E V ( ф , p ) - ^p— Z C k , V ( ф ) ⁽-^Jpp- ,

A V k - 0                 ^k !

2 V

t dt

ф где Ckv (ф) - 2 J cos kt - sin2v t dt (11)

Для вычисления интегральной составляющей по выражению (4) в области наблюдения q/p ≤ 1 ис- пользуется рекуррентное соотношение, связывающее три последовательные члены ряда:

Jm - Q - (m -1) Jm - 2

n

+ -°cos ф- Jm-1 n

где

Q = e

i π ( n - n ₀ n cos ϕ )

Таким образом, имея исходные значения J 0 и J 1 , можно вычислить все последующие значения J m .

• 1.    С использованием найденного решения были получены картины пространственной структуры поля для секторных отверстий с произвольными значениями радиуса и углового раствора. На рис. 1 представлена пространственная структура поля для секторного отверстия, симметрично расположенного относительно оси х и имеющего указанные параметры: R = 10.95 λ и ϕ = 2 π /3 (угловой раствор). Структура поля представлена в виде распределения Ф в трех плоскостях, удаленных от плоскости отверстия на расстояние r 2 = 180 λ , 200 λ и 230 λ . Расстояние от точечного источника до плоскости отверстия r 1 = 300 λ . В каждой плоскости значения Ф , соответствующие определенному значению угловой координаты ϕ o , откладываются радиально от центра в единицах. Каждая кривая соответствует определенному значению ρ o (удалению от центра). Кривые распределения Ф имеют асимметрию относительно оси у , что и понятно, поскольку само отверстие имеет такую же асимметрию. Все значения параметров и пропорции между ними выбраны для проведения модельных экспериментов при разработке защитных дифракционных экранов в микроволновом диапазоне радиоволн.

  

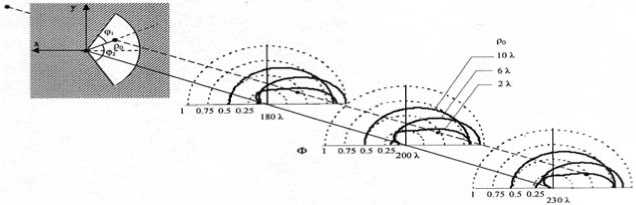
  Рис. 1. Геометрия задачи и пространственная структура множителя дифракционного ослабления Ф для секторного отверстия с радиусом R = 10,95 λ и угловым раствором φ = 2π/3 . Расстояния от отверстия до источника r₁ = 300 λ , до плоскостей наблюдения r₂ = 180 λ , r₂ = 200 λ , r₂ = 230 λ . Каждая кривая соответствует определенной удаленности от центральной оси: ρ 0 = 10 λ , ρ 0 = 6 λ , ρ 0 = 2

  
  

• 2.    В практике микроволнового радиодиапазона представляют интерес защитные экраны в виде полукруга [9] с радиусом, равным радиусу первой зоны Френеля в плоскости экрана относительно точек излучения и наблюдения, т. е. R = b 1 . Такие экраны в точке наблюдения на центральной оси, проходящей через центр полукруга, дают ослабление поля до нуля. Представляет интерес распределение поля в окрестности этих точек. На рис. 2 представлены для экрана в виде полукруга с радиусом R = 10.95 λ результаты расчетов дифракционной картины поля вблизи точки его минимального уровня, которые получены с использованием принципа Бабине [1] и найденного решения (3) для секторного отверстия. Для экрана с радиусом R = 10.95 λ расчетная точка наименьшего уровня поля находится на центральной оси на удалении r₂ = 200 λ от плоскости экрана, поэтому плоскость, в которой лежит эта точка, является главной. Структура поля представлена в виде пространственной картины распределения Ф в главной плоскости на r 2 = 200 λ и в трех других плоскостях, удаленных от плоскости отверстия на r₂ = 150 λ , r₂ = 180 λ , r₂ = 230 λ . В каждой плоскости значения Ф, соответствующие определенному значению угловой координаты φ 0 , откладываются радиально от центра в единицах. Так как экран является ослабляющим и обеспечиваемые им уровни поля достигают очень малых величин, здесь выбраны логарифмические единицы дБ. Каждая кривая соответствует некоторой удаленности ρ o точки наблюдения от центра.

Как видно из дифракционных картин поля, степень ослабления поля уменьшается по мере удаления от центральной точки и по оси, и в самой плоскости наблюдения. В главной плоскости (r₂ = 200 λ ) на небольшом удалении от центра ρ o = λ , ослабление достигает более -60 дБ, в то время как на удалении ρ o = 3 λ наблюдается ослабление порядка -20 дБ. То же самое можно отметить при сдвиге по оси. Дифракционная картина имеет некоторую асимметрию относительно вертикальной оси, которая усиливается при удалении от главной плоскости ослабления. Причем направление асимметрии зависит от положения точки наблюдения относительно главной плоскости ослабления.

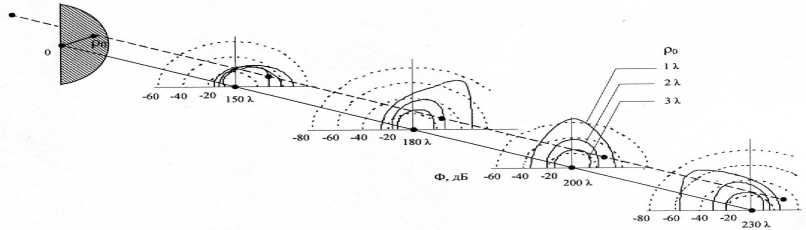
Рис. 2. Пространственные картины поля (множителя дифракционного ослабления Ф) для ослабляющего экрана в виде полукруга с радиусом R = 10,95 λ . Расстояния от отверстия до источника r₁ = 300 λ , до плоскостей наблюдения r₂ = 150 λ , r₂ = 180 λ , r 2 = 200 λ , r 2 = 230 λ . Каждая кривая соответствует определенной удаленности от центральной оси: ρ 0 = λ , ρ 0 = 2 λ , ρ 0 = 3 λ .

Таким образом, впервые получены результаты расчетов пространственной структуры дифракционного поля от секторного отверстия и от защитного экрана в виде полукруга. Использование в расчетах аналитических решений физической оптики [4, 5] дает возможность увеличить точность получения равномерной части дифракционного поля, что важно при решении различных практических задач, имеющих приложение в оптике и в микроволновой части радиоволн.