Расчет пространственного распределения мощности лазерного излучения для формирования требуемого энергетического воздействия

Самарский государственный аэрокосмический университет

Наиболее эффективные режимы обработки определяются только при решении обратной задачи теплопроводности, поэтому разработка математических моделей тепловых процессов при лазерной обработке требует новых подходов, учитывающих специфику создания требуемого энергетического воздействия на технологические объекты. Разработана методика расчета пространственного распределения мощности лазерного излучения, применение которой позволяет формировать более равномерное температурное поле по длине движущегося полосового энергетического источника. Для создания требуемого энергетического воздействия на технологические объекты целесообразно применять оптические системы на основе динамических фокусаторов излучения.

Теоретическое и экспериментальное изучение тепловых процессов в зоне энергетического воздействия позволяет выделить общие закономерности и определить основные направления совершенствования технологических процессов. Приближенные аналитические решения известных систем дифференциальных уравнений с соответствующими граничными условиями могут использоваться в относительно простых схематизированных моделях для проведения качественного и приближенного количественного анализа тепловых явлений. Возрастающие возможности вычислительных средств обуславливают широкое применение численных методов решения нестационарных трехмерных задач нелинейной теплопроводности. Известно, что наиболее эффективные режимы обработки определяются только при решении обратной задачи теплопроводности [1]. Поэтому разработка математических моделей тепловых процессов при лазерной обработке требует новых подходов, учитывающих специфику создания требуемого энергетического воздействия на технологические объекты.

При обработке деталей лазерным излучением характерны большие градиенты температур, смещение точек структурных и фазовых переходов, изменение в процессе обработки оптических и теплофизических свойств материалов [2]. Численное интегри- рование дифференциального уравнения теплопроводности проводится с учетом зависимостей от температуры теплофизических характеристик обрабатываемых материалов (теплопроводности, объемной теплоемкости, а также полной поверхностной теплоотдачи) и эффективного коэффициента поверхностного поглощения лазерного излучения.

Рассматривается нелинейная задача теплопроводности при нагреве технологического объекта полосовым поверхностным энергетическим источником. Расчет проводится с учетом реальной геометрической формы технологического объекта, который перемещается либо с постоянной линейной скоростью υ в положительном направлении оси Oy , либо с постоянной угловой скоростью ω в положительном направлении оси OΦ соответственно в системах координат (x, y,z) или (ρ,Φ,ς) , помещенных в центр энергетического источника мощностью Q . Принимается допущение: энергетический источник с заданными геометрией и пространственным распределением мощности является поверхностным и занимает область φ на поверхности исследуемого объекта. На остальной части поверхности задаются нелинейные условия теплообмена с окружающей средой. Для преобразования нелинейных уравнений теплопроводности в частных про- изводных в систему линейных алгебраических уравнений относительно температуры в дискретных точках исследуемого объекта используется метод конечного контрольного объема [3]. Основными этапами численного решения задачи являются дискретизация расчетной области – создание массива узлов; получение дискретных аналогов дифференциального уравнения теплопроводности методом контрольного объема; составление и приближенное решение системы алгебраических уравнений с неизвестными значениями температуры в каждом узле в рассматриваемый момент времени.

В работе [4] показано, что температура во всех узлах расчетной области в моменты времени, следующие с интервалом A t m , равна:

узловой точкой и соответствующими ей точками семиточечного крестообразного шаблона, при численном решении системы дифференциальных уравнений теплопроводности в прямоугольной системе координат определяются следующими выражениями ai-1, J,к = ki-1, J,к Ay AzI (§XL,J,K a+1, J, k = ki+1, J, kAу M (ax h, J, к ai,J-1,к = ki, j-1,к A Ax/(5У \J-1,к ai, J+1, к = ki, J+1, k Az Ax/ (5y ), J+1, к ai,J,к-1 = ki,J,к-1Ax AУ/(5z"it,J,к-1 ai, J, k+1 = ki, J, k+1Ax Ay/(5z )i, J, к +1

k , k

11-1, J, к I,       11+1, J, к I где    j i,J-1, к ^     j i,J+1, K i

Ii, J, к -1Ii, J, к+1J коэффициенты

гр m + 1

T i, j,к

HZ

g = 1

mm aa

I i-1 ,J,K I   \i-1 ,j,K I         \i +1 ,j,K I    \i +1 ,j,KI j i,J-1 ,k i ji,J-1 ,k i      ji,J+1 ,ki ji,J+1 ,ki

I i,Jk - 1 1   I i,J,K - 1 1         I i,J,K + 1 1    I i,J,K + 1 1

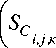
m

⁺ T i,J,K c V

m

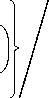
+AV,K i, j,к

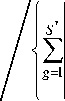
Or- . - i

I i - 1 ,J,k \ j i,J - 1 ,k i

I i,J,K - 1 |

+ afi+i /

\i+1,J,K I j ij+1 ,к i

I i j ,K + 1 |

^{+ A V}i,J,K c V ( TiJK ^^m ' ,

где T _{i ,} j _{, к} – температура, определяемая в узлах пространственной сетки;

i I

J I =1,2,

K I

r 1 1       1 1 1

। J । ; । J ।

I ^K I ’ I ^K I

– размерность индексно-

го пространственного массива; S * – размер тела; g - номер орта; m и _m + 1 - индексы двух последовательных моментов времени, промежуток между которыми равен A t _m ;

теплопроводности на гранях контрольного объема A V i , j , _K =A x A y A z ; ^{( S x} ) i - 1, j , к , ^{( S x} ) i + 1, j , к , ^{( б} У ) i , j - 1, к , ^{( 5} У L+1, к , ^{( S z} ) i , j , к - 1 , ^{( S z} ) i , j , к + 1 - расстояния между узловой точкой и соответствующими точками семиточечного крестообразного шаблона.

При решении системы дифференциальных уравнений теплопроводности в цилиндрической системе координат проводимости определяются уравнениями:

a i - 1,J , к = k i - 1, J , к P i - 1, J , k ^A^^A ^ ⁽M - 1, J , к

a i + 1, J , к   ^ki + 1, J , K ^p i + 1, J , к ^AФ^A ^ ^{( Sp )} i + 1, j , к

a i,J - 1, к = k i,J - 1, к ^A P ^A ^P i,J - 1, к ( ^{S Ф)} J - 1, K ^ai,J + 1, к = k i , J + 1, K ^A P ^A ^P i , J + 1, к ⁽⁸^\j^V к a i , J , к - 1 = ^ki, J , к - 1 P i, J , к-1 ^{AФA p (}_ 3^ ⁾ i , J , к - 1

i

^. (3)

a i, J , к + 1 = k i , J , к + 1 P i , J , к + 1 ^{AФA p (} 5?\ J , к + 1

^S C _{i , j , к} и ^S P _{i , j , к} – результат линеаризации воздействующего энергетического источника в виде S CP = S C ⁺ S Pa T J , к ;

i , j , к              i , j , к             ^{i , j , к}

A V j , _к    - контрольный объем;

aa

\ I - 1, J , к 1 ,       \ 1 + 1, J , к 1

j i , J - 1, к i   j i , j + 1, к i - проводимости между

I i , J , к - 1 I i , J , к + 1 J

Задача нахождения распределения мощности воздействующего энергетического источника, входящего в граничные условия уравнения теплопроводности второго рода, не всегда является корректной, поскольку ее решение не всегда однозначно и устойчиво. Для некорректных задач известен алгоритм [5], основанный на сужении области возмож- ных решений путем использования дополнительных априорных сведений относительно искомой функции и получивший название метода сведения к условно корректной задаче. Наиболее широко распространенным способом решения таких задач является метод подбора, подробно описанный в работе [5], заключающийся в решении прямых задач с итерациями на каждом шаге. Условием окончания итераций является совпадение с требуемой точностью заданного и полученного на k -ой итерации температурных полей, определяемых дискретными значениями температур в точках исследуемого объекта.

Условно-корректной постановке граничной обратной задачи теплопроводности удовлетворяют условие постоянства во времени плотности теплового потока, поскольку по истечении определенного времени температурное поле во внутренних точках исследуемого объекта регуляризируется [5, 6].

Пространственное распределение мощности q(x, y) задается в виде уравнения для полосового энергетического источника, что предоставляет возможность обеспечить условие однозначности решения, и определяется выражением fA(T)q(5u) при^е[-al2;02] ип<-Ь2;Ь2];

^ 0при ^ £ [ - a 2; a 2] или п ^- b( 2; bj 2],

(4) где A ( T ) – эффективный коэффициент поверхностного поглощения; где a , b – соответственно длина и ширина области φ , ограниченной прямыми 5 = - a /2;    ⁵ = al ²; п = ^- b ²; п = ^b /² ;

5 = x cos ф 1 - y sin ф 1 ; п = x sin Ф 1 + У cos Ф 1 ; ϕ ₁ – угол поворота светового пятна в фокальной плоскости.

Можно представить q ( ξ , η ) в виде уравнения

• -    2n       -2( n - 1)         -4 -2

q ^{5 , п} > = ^ 0 ( 0 ,1 ⁵ + 0 ,1- 1 5    + ... + a z 5 + a v ^ ⁺ al

• -    2 m       -2( m - 1)        -4 -2

' (^ 2 п + ^bn 2 - 1 п    + .• + ^п + ^ь1 п ^{+ b}0 ) ^{v ( 5 ,}п )

где q ₀ – плотность мощности в центре энергетического источника; 5 = 5 / 10 ^{- 3}м , п = п / 10 ^{- 3}м — безразмерные координаты; a n ! , a n 1 - 1 , ... , a 2 , ^a 1 , a 0 ; ^bn ₂ , ^b n 2 - 1 , ... , b 2 , b i , ^b 0 ^- коэффициенты полиномов (степенных многочленов); n ₁ , n ₂ – целые числа; ν ( ξ , η ) – дополнительная функция.

Совокупность значений температур в точках объекта воздействия определяется в соответствии с требуемым изменением его теплового состояния. На первом этапе целесообразно провести расчет пространственного распределения мощности воздействующего энергетического потока, обеспечивающего требуемую максимальную температуру термических циклов точек объекта, находящихся на заданной глубине по ширине зоны термического влияния.

Структурные превращения, протекающие при лазерном воздействии, определяются в большей степени не максимальной температурой, а совокупностью процессов нагрева, выдержки при определенной температуре и охлаждения, то есть термическим циклом. Поэтому, на втором этапе на основе выявленных закономерностей изменения температурного поля на поверхности и в объеме материала целесообразно определить условия достижения благоприятных термических циклов для получения заданных свойств объекта воздействия и провести коррекцию пространственно-временных характеристик лазерного воздействия с целью обеспечения требуемых температурно-скоростных режимов.

В соответствии с разработанной методикой расчета пространственного распределения мощности лазерного излучения обратная задача теплопроводности решается методом итераций, а определение требуемого распределения мощности содержит следующие этапы:

• -    определение допустимой максимальной температуры на поверхности исследуемого объекта, соответствующей проектируемому технологическому процессу;

• -    ввод первоначального значения распределения мощности воздействующего

энергетического источника и определение значение скорости перемещения энергетического источника, при которой максимальная температура на поверхности технологического объекта не превышает допустимую максимальную;

• -    ввод значения требуемой максимальной температуры на заданной глубине объекта вдоль линии перемещения энергетического источника;

• -    расчет значений максимальной температуры на заданной глубине технологического объекта;

• -    определение среднеквадратичного отклонения расчетной температуры от требуемой и сравнение его с заданным допустимым значением;

• -    коррекция распределения мощности потока энергии на поверхности технологического объекта;

• -    коррекция пространственно-временных характеристик лазерного воздействия (мощности, ее пространственного распределения, а также скорости перемещения энергетического источника) с учетом условий достижения благоприятных термических циклов для получения заданных свойств материала технологического объекта.

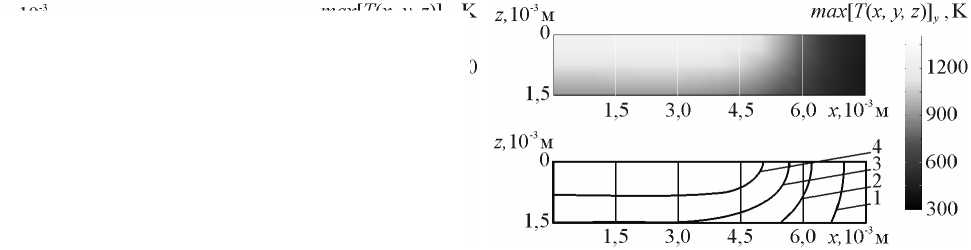
В результате расчета определено пространственное распределение мощности лазерного излучения q(x, y) для формирования требуемого энергетического воздействия на технологические объекты из хромоникельмолибденовой и цементируемой сталей, а также нагартованных алюминиевых и низколегированных титановых сплавов. Результаты расчета значений максимальных температур вдоль линии перемещения энергетического источника по поверхности технологического объекта из хромоникельмолибденовой стали представлены на рис.

Формирование определенного пространственного профиля интенсивности в заданной области на поверхности детали достигается только при использовании соответствующих оптических систем. Многообразие используемых и разрабатываемых оптических систем демонстрирует широкий интерес исследователей к этому важному вопросу, определяющему уровень совершенства лазерных технологий. В настоящее время созданы принципиально новые оптические элементы с ранее недостижимыми функциями – фоку-саторы излучения [7, 8]. Фокусаторы представляют собой дифракционные оптические элементы, имеющие регулярную структуру микрорельефа рабочей поверхности, определяемую в зависимости от заданной формы области фокусировки, распределения в ней интенсивности излучения и его длины волны. Отражающие фокусаторы осуществляют поворот пучка лазерного излучения и перераспределение энергии в различные геометрические фигуры с заранее заданным профилем интенсивности.

Для применения в технологических процессах лазерной обработки деталей фокуса-тор в виде отражающей пластины выполня-

б

Рис. Результаты расчета значений максимальных температур max [ T ( x , y , z )] _y вдоль линии

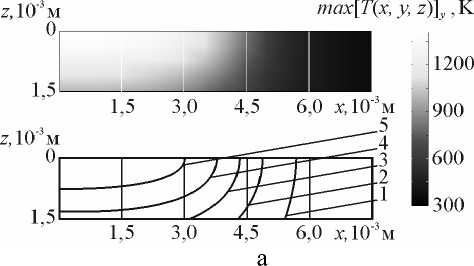
перемещения энергетического источника мощностью Q = 950 Вт, движущегося с постоянной скоростью υ = 1,1·10^-2 м/с по поверхности технологического объекта из хромоникельмолибденовой стали.

T , K: 1 – 600; 2 – 750; 3 – 900; 4 – 1050; 5 – 1200; k = 1 (а); k = 10 (б)

ется с возможностью перемещения (поворота, вращения, колебательного движения и т.д.).

Установлены закономерности перераспределения мощности сформированных лазерных потоков, а также изменения фокусного расстояния и длины фокального отрезка при изменении пространственного положения динамического фокусатора. При повороте оптического элемента происходит поворот лазерного пятна в фокальной плоскости, перераспределение мощности в фокальном отрезке и уменьшение средней величины ее плотности, увеличивается длина лазерного пятна и изменяется положение фокальной плоскости, что позволяет регулировать пространственное распределение мощности лазерного излучения и энерговклад в обрабатываемый материал.

Для регистрации температурных полей при воздействии на материалы высокоэнергетических потоков и применения в составе систем управления технологическими процессами создана система бесконтактной диагностики. Система содержит ИК-радиометр – блок оптической визуализации температурного поля в рабочей зоне тепловизора “Радуга” и устройство ввода-вывода видеоизображения на персональный компьютер. Устранение влияния диффузно-рассеянного лазерного излучения, уровень мощности которого может значительно превышать тепловое излучение нагретой области, достигается применением германиевого и сапфирового фильтров, ограничивающих спектральный диапазон пропускания полосой d λ = (2…7)∙10^-3 м.

В результате проведенных исследований установлено, что расчетные значения температур в обрабатываемых материалах при воздействии движущихся распределенных поверхностных источников энергии для выбранного класса материалов в исследуемых диапазонах скорости (υ = (2…30)∙10-3 м/с), мощности (Q=(0,2…1)∙103 Вт) и геометрических параметров энергетических источников удовлетворительно (погрешность δT ≤ 10…15%) коррелируют с результатами экспериментальных исследований. Воздей- ствие на объекты полосовых движущихся энергетических источников предоставляет возможность обеспечить выравнивание значений максимальных температур в поперечных сечениях зоны термического влияния в ходе термических циклов нагрева и охлаждения, а увеличение плотности мощности лазерного излучения по краям полосы компенсирует повышенный теплоотвод с периферийных участков. В зависимости от степени влияния технологических параметров обработки непрерывным излучением на величину и распределение температур их можно расположить в ряд:: мощность излучения Q , скорость перемещения лазерного пятна υ, его форма и пространственное распределение плотности мощности излучения на поверхности обрабатываемого материала. Применение фокусаторов излучения для создания требуемого энергетического воздействия на технологические объекты позволяет увеличить ширину зоны лазерной обработки без перегрева ее центральных участков.

Выводы

На основе математического моделирования тепловых процессов и использования методов решения обратной задачи теплопроводности разработана методика расчета пространственного распределения мощности лазерного излучения для формирования требуемого энергетического воздействия на технологические объекты. Установлено, что пространственное перераспределение мощности движущихся энергетических источников позволяет регулировать распределение температуры в зоне обработки.

Применение разработанной методики расчета пространственного распределения мощности лазерного излучения позволяет создать более равномерное температурное поле по длине полосового источника. Достигается выравнивание значений максимальных температур вдоль линии перемещения энергетического источника в центре и на периферии зоны термического влияния с увеличением ширины требуемых изотерм максимальных температур. Для создания требуемого энергетического воздействия на техно- логические объекты целесообразно применять оптические системы на основе динамических фокусаторов излучения.