Расчет расходов и уровней малых водотоков

Определение расходов и уровней водотоков с помощью гидравлических расчетов проводится для различных целей: планирования режимов работы водохранилищ, уточнения диспетчерских графиков управления водохранилищами, пропуска паводков, имитации редких гидрологических явлений и экстремальных ситуаций, режимов работы прирусловых гидротехнических сооружений, прогнозирования экстремальных (максимальных и минимальных) уровней. Для гидравлических расчетов уровня водотоков в

России, и за ее пределами широко используются программные продукты (гидравлические расчетные комплексы) разных авторов. Перечислим наиболее известные программные продукты:

MIKE (Датский институт гидравлических исследований);

HEC-RAS (Корпус американских военных инженеров);

SWAT (Департамент сельского хозяйства США);

SOBEK (Дельфтская гидравлическая лаборатория, Голландия),

EFDC (Институт морских исследований Вирджинии, США);

BASINS, HSPF, QUAL (Агентство по охране окружающей среды США).

Пользователям зачастую трудно определить, какой из них целесообразно применить в конкретных условиях. Сравнение характеристик перечисленных программных продуктов опубликовано в [1 – 3]. В трех указанных обзорах приведено 182 ссылки на описание особенностей программных продуктов, на исследования с их помощью гидрологических характеристик водотоков и качества воды в них.

Следует согласиться с мнением [4], что принципиальных отличий в математических методиках и в методике расчетов эти программы не имеют. Для установившегося движения водотока используется формула Шези, а для расчета не-установившегося движения уравнения Сен-Венана. Решение находится одним из численных методов, в большинстве программ – на основе конечно-разностных схем. Различия программных продуктов заключаются в основном в методах учета гидрологических параметров водотоков, формах ввода морфометрической информации, описания гидротехнических сооружений, вывода и визуализации результатов расчетов.

Существуют и российские программные продукты такого рода. Например, WPI-RQC (Water Problem Institute – River Quality Control), разработанная в Институте водных проблем ИВП РАН [5, 6], «Волна» научнопроизводственного предприятия ООО «Титан-Оптима» [7]. Однако они имеют узкую (специальную) направленность. С помощью [5] можно рассчитать перенос и трансформацию загрязнений от точечных и диффузных источников в разветвленной речной системе. Программа «Волна» [7] позволяет рассчитывать параметры волны прорыва и затопления местности, возникающей при авариях на гидросооружениях: максимальные глубина затопления, ширину затопления и скорость течения, время прихода фронта, гребня и хвоста волны прорыва, максимальный расход воды в створе, высоту волны.

Линейки программных продуктов, как правило, имеют не только версию для гидравлического расчета в одномерном приближении (например, MIKE-11), но и для решения задачи речной гидравлики 2D и 3D (MIKE-21, MIKE-31). Для решения гидравлических задач малых рек и ручьев, как правило, достаточно одномерных математических моделей. Поэтому в данной статье остановимся на программных продуктах, разработанных на базе одномерных уравнений

Сен-Венана. Одномерность означает, что гид-

равлические характеристики потока осреднены по поперечному сечению.

Разработана и широко используется од-

номерная математическая модель динамики течения в системе водотоков, как без боковой при-

точности, так при ее наличии, на основании уравнения Сен-Венана [8 – 10]:

д to   д Q

---+----= q д t   d X

a Q

— +

8 t

_d_l Q_ I д X to

V     7

+ g • to •

+ д X

V

Q'

K ² V

= 0

, (1)

где t – время, с;

X – расстояние вдоль оси водотока, м;

Q(X,t) – расход воды, м³/с;

to(X,t) - площадь живого сечения водотока, м²;

q(X,t) – интенсивность бокового притока, м²/с;

Z(X,t) – уровень свободной поверхности,

м;

g – ускорение свободного падения м/с²;

K – расходная характеристика русла, м³/с.

Начальные и граничные условия к систе-

ме уравнений (1):

Q ( X ,0) = f , ( X ) , to ( X ,0) = f ₂( X ) ;

Q ^(0, t ) = ф _х⁽ t ) , ^{to (0,} t ) = ф 2 ⁽ t ) . ⁽²⁾

Для решения краевой задачи (1 – 2) с помощью одного из программных продуктов необходимо подготовить и ввести обширную геодезическую информацию по сечениям реки, отметкам поверхности ее поймы и всего бассейна. Эта работа не представляет особой сложности лишь при наличии функционирования ГИС бассейна реки. В противном случае пользователю придется решать сложную проблему. Так в [10] данные о поперечной структуре сечений русла среднего течения Северной Сосьвы были подготовлены на основе данных о глубинах с лоцманских карт с помощью IT-технологии. При этом абсолютные ошибки оказались велики из-за низкого качества

исходных данных, получаемых с лоцманских карт для построения расчетной сетки модели. Вывод [10]: для создания адекватной информа-ционно-моделирующей системы прогноза гидрологических ЧС с использованием ресурса программного пакета MIKE-11, необходимо организовать полевые съемки высокого пространственного разрешения высотных отметок русла и поймы реки.

В [11] было предложено корректировать геометрические и гидравлические характеристики речного русла путем решения обратных задач (1 – 2). В дальнейшем этот процесс был назван

Н.Л. Великанов, В.А. Наумов, С.И. Корягин калибровкой базовой геометрической информацией цифровой гидравлической модели [12]. Этот процесс калибровки, включает этапы гидравлического расчета, сравнения полученных после расчета уровней с фактическими данными на постах наблюдений и оценку различий между ними, устранения этих различий путем изменения параметров сечений (ширины русла и пойм, глубины, шероховатости, расстояний). Критерием калибровки является максимальное приближение полученных по расчетам уровней и объемов водохранилищ к фактическим уровням реки на створах - постах наблюдений в соответствующих гидрологических условиях. Очевидно, что такой метод корректировки данных пригоден лишь для тех водотоках, на которых проводятся систематические гидрометрические наблюдения. Тогда как на малых водотоков стационарных постов наблюдений очень мало. В частности, на реке Новой в калининградской области систематических гидрометрических наблюдений не проводилось.

Рассмотрим расчет, выполненный в 2017 году при обработке результатов инженерногидрологических изысканий. Река Новая является левым притоком реки Преголи. Длина водотока L =10,1 км; средний уклон I = 2,2 %о; площадь водосбора A = 13,2 км ²; в том числе леса составляют А л = 12,7%; болота А б = 4,5 %. На рис. 1 показана приустьевая часть бассейна реки Новой. При проведении инженерных изысканий были выполнены промеры сечений водотока в 9 створах, расположенных примерно через 1 км. Довольно большое расстояние между створами было обусловлено плавностью изменений русла по длине водотока, что иллюстрируется отметками дна на рис. 2 и 3.

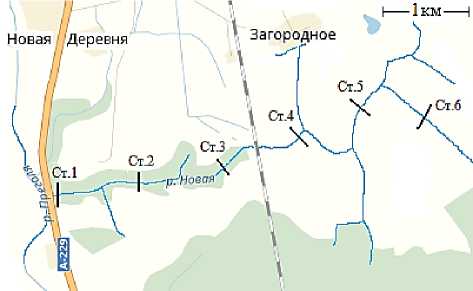
Рисунок 1 - Часть бассейна реки Новой с промерными створами

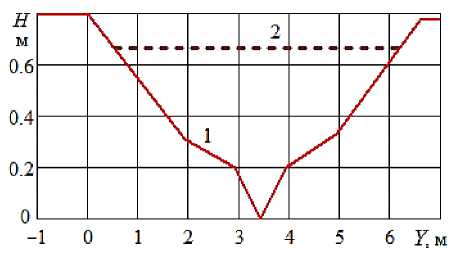
Рисунок 2 - Поперечное сечение реки Новой в створе № 1 : 1 - отметки дна, 2 - максимальный расчетный уровень Р = 10 %

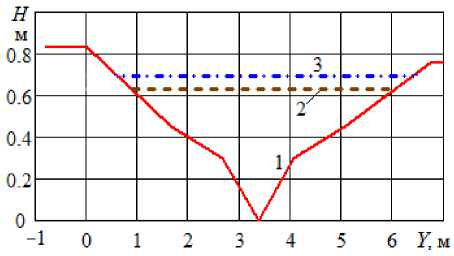
Рисунок 3 - Поперечное сечение реки Новой в створе № 2: 1 - отметки дна, 2 - максимальный расчетный уровень Р = 10 %; 3 - Р = 5 %

Следующим этапом была определена интенсивность боковой приточности реки Новой во время весеннего половодья с использованием формулы редукционной [13]:

К„ • h • ц • б • 5, • 5, • A ( X )

Q p % ( x ) =                        --------, (3)

( A ( X ) + A ,)

где Q p% - максимальный расход воды весеннего половодья, заданной ежегодной вероятности превышения на расстоянии X от истока, м³/с;

nr - показатель степени редукции, для всей территории Калининградской области принят nr = 0,18;

K o - параметр, характеризующий дружность половодья;

h p - слой суммарного стока половодья той же обеспеченности ( Р% ) , что и искомый максимальный расход воды;

ц - коэффициент, учитывающий неравенство статистических параметров слоя стока и максимальных расходов воды;

5 1 , 5 2 - коэффициенты, учитывающие снижение максимального расхода воды соответственно лесами и болотами;

5 - коэффициент, учитывающий влияние на сток озер, водохранилищ;

А - площадь части водосбора на расстоянии X от истока, км²;

А 1 – дополнительная площадь, учитывающая снижение интенсивности редукции модуля максимального стока с уменьшением площади водосбора, км².

Коэффициент δ 1 определялся по формуле [13]:

3 1 = a 1 / (А л + 1) 0,22 ,                   (4)

где α 1 – параметр, учитывающий расположение леса на водосборе;

А л - залесённость водосбора в процентах.

Коэффициент δ 2 определяется по формуле [13]:

3 2 = 1 - в- lg (0,1 • А б + 1),           (5)

где β – коэффициент, учитывающий тип болот и состав грунтов, для рассматриваемых водосборов и равен 0,8;

Аб – заболоченность водосбора в процентах.

Интенсивность боковой приточности может быть найдена для заданной обеспеченности по формуле:

q p % ( X ) =   "" '   .                     (6)

dX

На рис. 4 представлены результаты расчета уровня воды в реке Новой во время весеннего половодья при различных значениях обеспеченности. Видно, что при Р = 10 % затопления нет; при Р = 5 % затопление произойдет около отметки 10 км (недалеко от створа № 1), а при Р = 1 % – после отметки 6 км.

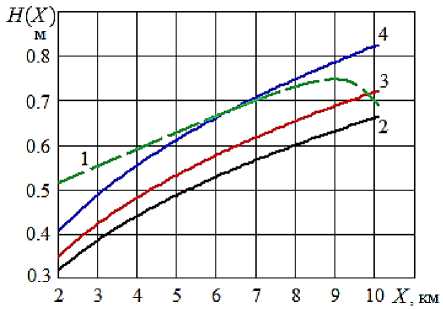
Рисунок 4 – Максимальные расчетные уровни весеннего половодья вдоль реки Новой : 1 – уровень затопления, 2 – расчетный уровень, Р = 10 %; 3 – Р = 5 %; 4 – Р = 10 %