Расчет распределения температуры в ребре постоянного поперечного сечения при радиационном отводе тепла с его поверхности

В монографии ( Керн, Краус , 1977) представлен всесторонний математический анализ процессов переноса тепла через различные стенки, оснащенные ребрами разной конфигурации. При этом рассмотрены главным образом задачи, относящиеся к классу линейных. Однако на практике имеют место случаи, когда тепловой поток, отдаваемый ребристой поверхностью, является нелинейной функцией его температуры. Так, например, возможен процесс радиационного охлаждения в среде с температурой близкой к нулю (в условиях вакуума).

Такая задача, представляющая определенный инженерный интерес, может быть теоретически сформулирована следующим образом d2T     fT4   0, dx2   XP,

T = T0 при x = 0, dT

0 при x = l , dx

где T = T ( x ) – искомое распределение температуры вдоль оси ребра, К; T 0 – абсолютная температура основания ребра, К; λ – коэффициент теплопроводности материала, Bm/мK; σ – видимый коэффициент теплообмена излучением, Bm/м²K⁴; P , f – периметр и площадь поперечного стержня соответственно, м, м²; l – длина ребра, м.

2.    Результаты исследований

Целесообразно систему (1-3) привести к безразмерному виду.

T       x         Pl ²

Если ввести безразмерные комплексы 3 = — ; X = — ; Sk-----T 3, где Sk - число Старка, то

T 0           l             f ⁰

система (1-3) преобразуется к виду d2! = Sk э4, dX2

В = 1 при X = 0, ^- = 0 при X = 1. dX

Так как дифференциальное уравнение (4) является существенно нелинейным, получить его строгое аналитическое решение весьма затруднительно. Поэтому целесообразно применить к задаче (4-5) наиболее эффективный приближенный аналитический подход. Для ослабления нелинейности в уравнении (4) может быть применен метод интегрального линейного преобразования, предложенный в работе ( Видин , 1992). Для этого нужно ввести новую зависимую переменную, связанную с искомой температурой В ( X) соотношением

u =f d ?  1

Тогда система (4-6) запишется следующим образом dXdU -sk=о, dX 2      dX

U = 0 при X = 0, dU = 0 при X = 1. dX

dU ²

Если в первом приближении функцией F ( X )  4 ³

, входящей в уравнение (8),

пренебречь, то нетрудно получить решение в форме

U = SkX\ — -1 |.

Отсюда с учетом (7) следует, что

а =

1  3 SkX 1 ^X

•

Так как комплекс F ( X )  4 ³

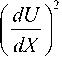
является на отрезке (X = 0-1) положительной величиной, т.е. представляет собой некоторый условный дополнительный тепловой источник в стержне, то, очевидно, что выражение (12) дает заниженное значение искомого распределения температуры В (X) при X > 0. Наименьшая величина безразмерной температуры ребра будет на его вершине (при X = 1). Эта температура согласно (12) равна з . = min

1   ³ Sk

Если теперь в уравнение (8) подставить вместо комплекса

dU ²

F ( X ) = 4В³1 -^ I приближенное

значение F ( X )  4 ³

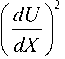
оно примет вид

d ² U     4     dU ²

Sk 0

dX ²     3     dX

1 Sk

Видин Ю.В., Казаков Р.В. Расчет распределения температуры…

Обозначим dU

_W d_dU_{X ,}

причем

W = 0 при X = 1.

Для новой переменной W дифференциальное уравнение (14) запишется ^{dW     8} W ² Sk 0 .

dX  23 Sk

Интегрируя дифференциальное уравнение (17) с учетом условия (16) можно получить следующее аналитическое решение

W

— 4 j	^Sk M x A
exp (2 + 3 Sk ) Sk exp 4	(1    x )  1 23 Sk

8              2Sk exp 4          (1  x) +1

23 Sk

.

Формулу (18) также можно представить в более удобном виде через гиперболический тангенс ( Бронштейн, Семендяев , 1965)

W     (2 ± 3 Sk ) Sk

₂    2 Sk

2+ 3 Sk

(1 X )  .

Затем на основе выражения (15) легко установить зависимость для функции U ( Бронштейн, Семендяев , 1965)

23 Sk U         ln

ch	8 Sk  (1 X ) 23 Sk

8 Sk ch

23 Sk

.

Используя это решение, удается окончательно установить нижнюю границу для искомого температурного поля рассматриваемого тела наим.

1+ 3(2 ± 3 S ) _ln

ch	8 Sk 23 Sk

8Sk ch         (1 X )

23 Sk

.

Аналогичным образом находится верхняя граница для функции ϑ = ϑ (X). С этой целью уравнение (8) записывается в виде d2U +4dU Sk 0, dX 2    dX

т.е. фиктивный тепловой источник в стержне F ( X ) берется по максимально возможной величине. Интегрируя систему (22), (9-10) подобно тому, как это было изложено ранее, находится новое соотношение для переменной U

1 ch 2 Sk (1 X )

ch 2 Sk

.

Отсюда следует, что формула для расчета верхних граничных значений искомого распределения температуры будет иметь вид

9,

наиб .

1+3ln

ch2Sk ch2 Sk (1 X )

.

Проведение практических расчетов по зависимостям (21) и (24) не представляет затруднений, так как гиперболические функции подробно затабулированы ( Сегал, Семендяев , 1962).

В таблице представлены результаты вычислений безразмерной температуры в сечении X = 0,5 и X = 1 для чисел Старка Sk = 0,1; 0,5; 1,0.

Таблица

X	Sk = 0,1		Sk = 0,5		Sk = 1,0
	ϑ наим.	ϑ наиб.	ϑ наим.	ϑ наиб.	ϑ наим.	ϑ наиб.
0,5	0,963	0,968	0,881	0,892	0,813	0,843
1,0	0,957	0,957	0,848	0,858	0,767	0,795

3.    Заключение

На основе результатов, представленных в таблице, можно сделать ряд выводов:

• 1.    Различие между ϑ наим. и ϑ наиб. при небольших числах Sk почти отсутствует.

• 2.    С ростом величины Sk различие между ϑ наим. и ϑ наиб. возрастает. Однако по абсолютной величине невязка дз = з наиб — Э¹ оказывается с инженерной точки зрения небольшой.

• 3.    Очевидно, что среднее арифметическое значение температуры о = ^{наиб . наим .} будет обладать

высокой точностью при любом значении числа Sk .