Расчет режимов сварки с использованием современного программного обеспечения

Модернизация современного сварочного производства неразрывно связана с применением компьютерных технологий. Основной технологической задачей сварочного производства является выбор оптимального способа сварки и его режимов по заданным геометрическим параметрам и прочностным характеристикам соединения. Критериями оптимизации являются формирование шва, свариваемость металла и стабильность качества при наличии существующих физических и технико-экономических ограничений.

Сложная проблема оптимизации технологических процессов сварки может быть решена на основе эмпирических и теоретических моделей, а также их комбинаций.

В условиях ограниченного доступа к экспериментальным стендам весьма полезной является возможность моделирования сварочных режимов на основе материалов, ранее полученных и опубликованных в открытой печати.

Для указанных целей целесообразно использование математического пакета MathCAD, предназначенного для решения инженерных технических и технологических задач. Математический пакет MathCAD выгодно отличается от других пакетов простотой синтаксиса и относительной легкостью изучения. Это позволяет сосредоточить внимание инженера на логике методов и алгоритмов расчетов, освобождая его от необходимости освоения громоздких и плохо запоминающихся вычислительных процедур. В то же время MathCAD является мощной системой компьютерной математики, сочетающей в себе визуально ориентированный входной язык, удобный редактор текста и формул.

На кафедре «Оборудование и технология сварочного производства» Южно-Уральского государственного университета (ОиТСП ЮУрГУ) математический пакет MathCAD используется для решения некоторых инженерных задач, а также в учебных целях.

В частности, математический пакет MathCAD используется при изучении тепловых процессов сварки путём построения термических циклов и температурных полей в металле при воздействии мгновенного точечного источника тепла. Дополнительно производится сравнение температурных полей и термических циклов для массивов с разными теплофизическими показателями: стали, меди и т. п. В дальнейшем аналогичные упражнения вы- полняются для движущегося и быстродвижущегося источников тепла. При этом в объем заданий входит вычисление размеров зоны оплавления, мгновенной скорости охлаждения на оси шва и на границе оплавления, продолжительности пребывания металла при температуре выше заданной и т. п.

Для инженеров и специалистов сварочного производства может представлять интерес возможность использования математического пакета MathCAD для оперативного расчета и оптимизации сварочных режимов.

Известные коммерческие программы вследствие скрытого алгоритма вычислений имеют ограниченные рамки применения и используются главным образом сотрудниками проектных организаций для укрупненной оценки энергетических и материальных затрат. Скрытый и недоступный для коррекции алгоритм расчета не позволяет использовать коммерческие программы для моделирования сварочных процессов и оптимизации режимов сварки.

В настоящее время известно множество методик расчета режимов сварки плавлением [1–5], в числе которых наиболее известна методика А.И. Акулова, Г.А. Бельчука и В.П. Демянцевича, однако они построены на эмпирических формулах и диаграммах, что затрудняет их использование для компьютерного моделирования режима сварки в условиях многообразия требований, предъявляемых к сварным соединениям. Кроме того, существующими методиками предусмотрены технологические ограничения, которые накладываются на промежуточные результаты, что требует принятия логических корректирующих решений, обращенных к начальным стадиям расчета (обеспечение требуемых геометрических размеров, ограничение мгновенной скорости охлаждения и пр.), что также затрудняет компьютерное моделирование сварочного процесса. В частности, широко распространенный вариант графоаналитического расчета режимов сварки предусматривает следующие шаги:

• -    оценочное определение площади наплавленного металла в зависимости от толщины изделия и выбранного типа сварного соединения;

• -    определение скорости сварки из уравнения материального баланса;

• -    определение погонной энергии сварного шва;

• -    определение расчетных значений глубины провара, ширины шва и высоты валика.

Однако после определения расчетных значений ширины шва и высоты валика выясняется, что они отличаются от ранее принятых значений, и потому площадь наплавленного металла не соответствует значению, принятому при вычислении скорости сварки, что ведет к нарушению материального баланса и, соответственно, конфликту промежуточных результатов вычислений. Расхождение обычно превышает допустимые 5–7 %, при этом повторные вычисления формального харак- тера не всегда приводят к уменьшению расхождения и, как правило, требуют принятия интуитивных решений.

Кафедрой ОиТСП ЮУрГУ предложена расчетная модель режимов сварки, при реализации которой величина площади наплавленного металла строго согласована с геометрическими характеристиками сварного соединения и расчетными параметрами режима сварки, что исключает возникновение указанной выше ошибки вычислений.

Для составления схемы расчета необходимо выделить параметры режима, которые необходимо обязательно выполнить в соответствии с конструкторской или технологической документацией, а также расчетные параметры и вспомогательные информационные показатели. Поскольку глубина провара однозначно задается конструкторской документацией, она принята в расчетной схеме строго задаваемой величиной. Остальные геометрические параметры шва (ширина шва, высота усиления) могут быть скорректированы в ходе расчета с учетом выбранного типа сварного соединения, вводимых ограничений на мгновенную скорость охлаждения или по иным причинам, что позволяет отнести их к группе расчетных параметров.

Основными параметрами режима сварки под флюсом, оказывающими влияние на размеры и форму шва, являются диаметр электрода, сварочный ток или плотность тока в электроде, род и полярность тока, напряжение на дуге, скорость сварки. Из перечисленных технологических параметров к задаваемым следует отнести диаметр электрода (электродной проволоки), что обусловлено дискретным характером его номенклатурных значений по ГОСТ 2246–80. Значения сварочного тока и скорости сварки могут достаточно легко корректироваться при настройке режима, поэтому их целесообразно отнести к группе расчетных технологических параметров.

В конечном итоге, система уравнений для расчета режима сварки включает четыре задаваемых параметра – глубина провара, диаметр электродной проволоки, род и полярность тока, тип сварного соединения по ГОСТ 8713–79 и четыре расчетных параметра – величина сварочного тока, скорость сварки, ширина шва, высота валика. Остальные параметры режима сварки являются зависимыми и могут быть определены по результатам решения системы уравнений.

Начальное присвоение скорости сварки выполнено из условия оптимального значения произведения сварочного тока на скорость сварки, являющегося условием удовлетворительного формирования сварного шва [3].

Значения напряжения на дуге, коэффициента расплавления электрода, коэффициента наплавки, коэффициента влияния рода и полярности тока, коэффициента провара и погонной энергии опре-

Сварка, родственные процессы и технологии

делены как функции двух переменных: диаметра электрода и величины сварочного тока с тем, чтобы в ходе промежуточных вычислений значения указанных параметров оставались корректными. Коэффициенты расплавления и наплавки определены путем оцифровки диаграммы, моделирующей функцию двух аргументов (диаметра электрода и величины сварочного тока). Программа расчета коэффициента расплавления была подготовлена в рамках подготовки к студенческой научной конференции НИРС путем аппроксимации и интерполяции диаграммы [3].

Система уравнений включает известные уравнения [3]:

a ( d , I ) • I • 10 3

• ^V = ( F h ( h ) + 0,73 • b • g ) ^p ;

  h = 0,076

  
  

  f U ( d ^, I ) • I •n ____V____

  
  

  \ 0,5

  • 0,01 • 3600

  
  

  ¥ ( d , I )

  
  

• b = h •¥ ( d , I );

• ¥ ( d , I ) = 2,2,

где h , V , n — соответственно глубина провара, скорость сварки и коэффициент использования тепла при сварке под флюсом ( n = 0,85); a, F _н( h ), b , g -соответственно коэффициент и площадь наплавки без учета площади валика, ширина и высота усиления шва.

Последнее уравнение позволяет задать требуемый коэффициент формы провара в соответствии с конструктивно задаваемыми размерами сварного соединения. Для расширения области применения рассматриваемой модели в состав системы можно вводить уравнение ограничения мгновенной скорости охлаждения и др.

Серьезные затруднения в алгоритме расчета вызывала величина площади наплавленного металла, поскольку она зависит от режима сварки, типа сварного соединения и толщины изделия. Для включения ее в алгоритм расчета были определены функциональные зависимости площади наплавленного металла от толщины изделия для всех типов сварных соединений по ГОСТ 8713–79. Указанные зависимости определены студентами в ходе подготовки конференции НИРС известными методами математической статистики по усредненным значениям допустимых отклонений.

Для использования величины площади наплавленного металла в алгоритме расчета получены ее регрессионные зависимости от типа сварного соединения и толщины металла. Указанные зависимости получены по результатам обработки геометрических параметров всех типов сварных соединений по ГОСТ 8713–79.

Площадь наплавленного металла в системе уравнений представлена в виде суммы площади сечения разделки с зазором и площади валика:

F = Fн(h) + 0,73·b·g, что позволяет упростить расчетную модель.

Указанные зависимости представлены на рис. 1 и в табл. 1. Анализ показывает, что параметры сечений разделки с удовлетворительной точностью могут быть аппроксимированы квадратичными, а в некоторых случаях и линейными уравнениями.

Рис. 1. Зависимость площади наплавки от толщины изделия для двух типов сварных соединений по ГОСТ 8713–79 (фрагмент)

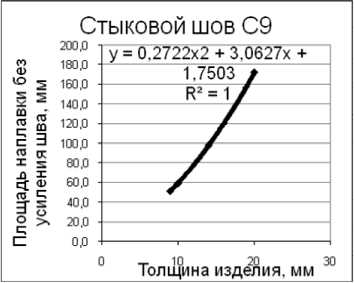
Таблица 1

Зависимости площади наплавленного металла (без учета площади сечения усиления шва) от типа стыкового сварного соединения и толщины основного металла (фрагмент)

Тип сварного соединения	Уравнение	Коэффициент корреляции
С47	F C47 = 0,373 s + 0,4502	0,988
С4	F C4 = 0,0381 s 2 + 2,0149 s – 3,5925	0,982
С34	F C34 = 0,1799 s 2 + 14,446 s + 98,098	0,998
С9	F C9 = 0,2722 s 2 + 3,0627 s + 1,7503	1

Использование выявленных таким образом закономерностей позволяет в оперативном порядке выполнять расчет режимов сварки для различных типов сварных соединений.

Результаты вычислений выводятся в виде матрицы или таблицы, в которой сведены все параметры сварного соединения и режима сварки, а также все вспомогательные информационные показатели, которые могут быть использованы для оценки материальных и энергетических затрат (рис. 2).

Таблицу расчетных параметров удобно использовать для анализа и оптимизации режимов сварки. Корректировка режимов может производиться изменением диаметра электрода, рода и полярности тока, типа сварного соединения или желаемого значения коэффициента формы шва.

Сопоставление расчетных режимных параметров с экспериментально полученными результатами указывает на их удовлетворительную сходимость и возможность использования представленной модели для практических расчетов с целью оптимизации сварочных режимов (табл. 2).

Представленная расчетная модель может быть распространена на иные методы сварки оплавлением путем дополнения ее соответствующими расчетными схемами.

Математический пакет MathCAD может быть использован для оперативной корректировки режимов с целью исключения холодных трещин, вызванных образованием закалочных структур, для определения размеров зоны перегрева, для прогнозирования геометрии сварных швов.

	0	1	2	3
0	"d, мм"	"h, mm"	"b, мм"	"g, mm"
1	5	10	22	3.28
2	"I, A"	"Imax, A"	"Imin, A"	"U, B"
3	908.47	989.48	575.29	40.31
4	"n"	"ф"	"ар, Г/(А*Ч)"	"а, гДА^ч)"
5	0.8	0.05	14.08	13.37
6	"Сталь"	"co мак, град/с"	"to мин"	"to, град/с"
7	"30XMA"	10	0.1

Рис. 2. Таблица результатов расчета режима сварки на дисплее ПК

Таблица 2

Сопоставление расчетных и экспериментально полученных данных

Параметры режима	Режим 1	Режим 2	Режим 3	Режим 4
	эксперимент расчет	эксперимент расчет	эксперимент расчет	эксперимент расчет
Диаметр электрода, мм	5 5	5 5	4 4	4 4
Сварочный ток, А	550...600 545	650...700 613	560...600 547	730...770 700
Напряжение дуги, В	34...36 32,2	32...36 33,7	35...36 33,7	38...41 37,5
Скорость сварки, м/ч	34...36 36	28...30 23	50...52 45,5	50...52 34,7
Глубина провара, мм	4,5 4,5	6,5 6,5	4,5 4,5	7 7
Ширина шва, мм	18 18	23 23	15 15	18 18
Высота усиления шва, мм	2,5 1,6	3,7 2,2	2,2 1,4	2,5 1,9
Площадь наплавки, мм2	30 27,5	60 48,4	22 21,9	31 36,6

Сварка, родственные процессы и технологии