Расчет резонансных частот ультразвуковой многослойной камеры с пьезоэлектрическим излучателем

В работе [1] рассматривались различные аспекты звуковых полей в многослойных ультразвуковых жидких резонаторах. Большое внимание уделялось рассмотрению резонансных явлений в камере. Однако при этом остался в стороне вопрос влияния излучателя как системы с распределенными параметрами на частотный характер поля во всей системе, включая и излучатель. В настоящей работе в качестве такового рассматриваются пьезоэлектрические излучатели, нашедшие широкое применение в ультразвуковых технологиях. Ранее подобная проблема рассматривалась в целом ряде работ [2–5 и др.]. В настоящей работе метод, предложенный для систем с идеальными границами [2, 5], адаптируется к случаю произвольных граничных условий.

Как известно, колебания в пьезоэлектриках, являющихся существенно анизотропными как с точки зрения механических, так и с точки зрения пьезоэлектрических и диэлектрических свойств, описываются сложной системой электромеханических уравнений. Эти уравнения однако существенно упрощаются в некоторых случаях, когда система уравнений становится одномерной. В настоящей работе рассматривается пьезоэлектрический излучатель в виде тонкой пластинки, осуществляющей только продольные колебания по толщине пластины. Все функции, описывающие электромеханические процессы такой пластины, зависят только от одной переменной x , ориентированной по толщине пластины, а тензоры преобразуются в константы. В этом случае линейные уравнения пьезоэлектричества описываются следующими уравнениями [2, 6]:

∂ ² u ( x , t )      ∂ ² ϕ ( x , t )      ∂ ² u ( x , t )

c∂x2+e∂x2=ρ ∂t2,(1)

e

ϕ(x,t)=u(x,t)+φ1x+φ0,(2)

ε

∂ u ( x , t )     ∂ ϕ ( x , t )

T(x,t)=c         +e ,(3)

∂ x ∂ x

D(x,t) =e∂u(x,t) -ε∂ϕ(x,t).(4)

∂ x ∂ x

Здесь u — смещение; ϕ — электрический потенциал; T — напряжение; D — диэлектрическое смещение; р , c , e , е — плотность, упругая жесткость пластины и ее пьезоэлектрическая и диэлектрическая постоянные соответственно, остающиеся неизменными в пределах пластины (здесь под диэлектрической постоянной в системе СИ понимается произведение электрической постоянной ε ₀ = 8.85418782 ⋅ 10 ^{- 12} Ф/м и безразмерной диэлектрической проницаемости материала); φ ₀ , φ ₁ — неопределенные константы.

Объединяя (1) и (2), имеем:

e ² ∂ ² u ( x , t )       ∂ ² u ( x , t )

(c +)          =ρ .(5)

ε    ∂x2

Решение (5) при установившихся гармонических колебаниях u ( x , t ) = u ( x ) e ^{- i ω t} имеет вид

u(x) =Acoskx+Bsinkx.(6)

Здесь A, B — неопределенные константы; k = волновое число; c — скорость продольной волны

c =

~     2 / c + e 2 / £

.

(6а)

ходя из (2)–(4), (6) и (10)–(13). Окончательно имеем:

Из (2), (3) и (5) имеем:

T(x ) = k ( ё + e 2 / £ ) ( - A sin kx + B cos kx ) + е ф 1 .

Из (2) и (4) имеем:

D ( x ) = -£ф 1 .

Пусть толщина пластинки — l , и величина x меняется в интервале x e [0, l ]. Для нахождения четырех неопределенных коэффициентов A , B , ф ₀ и ф 1 необходимо удовлетворить краевым условиям, например на границе x = 0 для всех искомых функций положить:

M uu = M Tr = cos kx ,	(15)
M uT = sin kx	(16)
y k
MTu = -y k sin kx ,	(17)
M Ф = MTD = e ( cos kx - 1 ) ,	(18)
£
e sin kx M Ф 1 = MuD =-- ,	(19)
£ y k
e 2 sin kx x M V D =-7--- ,	(20)
£  y k    £
у = ё + e 2 / £ ,	(21)

u ⁽ x )l x = 0 = u 0 ;        ^{ф (} x )| x = 0 = ^ф 0 ;

T ( x )| x = 0 = T 0 ;       D ( x )| x = 0 = D 0

В работе [2] приведены выражения, связывающие условия (9) с неопределенными коэффициентами. Применительно к рассматриваемому случаю они равны:

A = u 0 ,                               (10)

e

T +- D 0 I , £ J

e ф0   ф0     u 0 ,

£ ф1 =—1D0. £

После определения констант(10)–(13) можно использовать метод переходных матриц для расчета значений u ( x ), T ( x ), ф ( x ) и D ( x ) в любой точке x e (0, l ] [2]:

^ u ( x ) T ( x ) Ф ( x )

v D ( x ) J

^ Mulu	M uT	0	Mu 13 >	' u (0) ^		' u (0) ^
MTu	MTT	0	MTD	T (0)	= M	T (0)	(14)
M ф и	M ^ T	1	M » D	Ф (0)	p	Ф (0)	.
V 0	0	0	1 J	V D (0) J		V D (0) J

Последняя строка матрицы следует из (8). Найдем остальные элементы переходной матрицы, ис-

Пусть к обеим сторонам пластины приложены идеальные электроды, механические свойства которых могут быть проигнорированы. В этом случае искомые величины на разных сторонах левого электрода связаны соотношением [2]

T

^Ф I ^D J

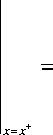
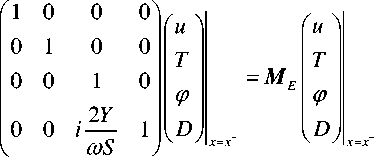
Здесь x — координата электрода; верхний индекс + или - относится к правой или левой стороне тонкого электрода соответственно; S — площадь электрода; Y = I / U — адмитанс (проводимость) цепи из двух электродов с находящейся между ними пьезоэлектрической пластиной; U и I — напряжение и ток в этой цепи. Как видно из (22), все величины, кроме электрического смещения D , в точке расположения электрода не меняют своих значений. Смещение D меняется скачком.

Если рассматривается система электрод— пьезоэлектрическая пластина—электрод , то совокупная переходная матрица M * равна произведению [2]

M * = M E • M p • M E , а (14) преобразуется к виду

^ и ( x ) ^л T ( x ) ф ( x ) I D ( x ) J

< M * ии	M * uT	M * и ф	M * uD ^	' и (0)'
M * Tu	M * TT	M * T ф	M * TD	0
M * ф и	M * ф T	M * фф	M * ф D	ф (0)
v M * Du	M * DT	M * D ф	M * DD ,	1 0 J

= M *

' и (0) '

T (0) ф (0) I D (0) J

Матрица M * в отличие от матрицы M p в (14) в общем случае не имеет специального вида с нулями и единицами в четвертой строке и третьем столбце.

В работах [2-4] функция Y ( ю ) определялась из характеристического уравнения, полученного из условия того, что левая и правая границы системы излучатель—жидкий резонатор являются свободными, т. е. значения упругого напряжения на этих границах равны нулю. В работе [1] рассматривался жидкий резонатор с потерями, когда правая граница не свободная, а на ней задано импедансное условие. В настоящей работе также предполагается наличие импедансного условия на правой границе резонансной системы, поэтому предлагается иной алгоритм расчета электрического адмитанса Y ( ю ).

Поставим краевые условия. На левой обкладке левого электрода и на правой обкладке правого электрода электрическое смещение равно нулю

D (0) = D ( l ) = 0.

Кроме того, примем, что левая граница свободная, т. е.

T (0) = 0 .

Напряжение на правой границе должно удовлетворять краевому условию (см., например, [7, с. 155])

T (l, t) =- Za        , dt или с учетом временного фактора e-imt

T ( l ) = iюZ_au ( l ).                  (24)

Здесь Z a — волновое сопротивление акустической нагрузки на правом торце пластины.

Начальный потенциал электрического поля определим через подаваемое на электроды напряжение Ue - ю ф (0) = Ц2.

Соответственно, исходя   из   условия    U =

= ф (0) - ф ( l ), имеем

U

ф(l) = - —.

Очевидно, что последнее равенство при подстановке в (22) обеспечивает скачкообразное падение электрического смещения D до нуля на правой стороне правого электрода.

После этого совокупность известных краевых условий можно записать так

D (0) = D ( l ) = 0,   T (0) = 0,

T ( l ) = itoZ a u ( l ),

UU

ф ⁽⁰⁾=—,   ф ⁽ l ) = ^- y.

С учетом (25) выражение (23) на границе x = l можно переписать в виде

^ и ( l )	>
iюZau ( l ) - U /2 v 0         J ' M * uu		M * uT   m * и ф   M * uD л	' и (0) ^
_ M	* Tu	M * TT   M * T ф   M * TD	0
M v M = M *	* фи Du ' и (0) 0 и /: 1 0	M * ф T  M * фф M * ф D M * DT M * D ф M * DD , "  . J	ф (0) 1 0    J	(26)

Для решения задачи (26) необходимо задание неизвестных пока значений начального смещения и (0) и адмитанса Y ( ю ). Вытекающая из (26) система четырех уравнений для определения двух неизвестных и (0) и Y ( ю ) переопределена. Анализ показывает, что для однозначного определения величин и (0) и Y ( ю ) можно использовать любое из вытекающих из (26) линейно зависимых уравнений:

M ∗Duu(0) + M ∗Dϕ U =0(27)

или

M∗ϕuu(0)+M∗ϕϕU=-U(28)

и уравнение

M ∗Tuu(0) + M ∗TϕU =iωZu(l).(29)

2 ^a

Будем использовать для определения искомых величин уравнение (29) и, например, (27). Для этого предварительно выразим коэффициенты (10)– (13) через искомые величины. Поскольку наличие электродов изменяет только электрическое смещение, а фигурирующая в (11) и (13) величина D ₀ есть электрическое смещение на правой стороне левого электрода, которое равно [2]

D0 = i     ,(30)

ωS то выражения (10)–(13) могут быть переписаны так:

A=u(0),(10а)

_    1 <  е _      . 1 е U

B=T+eD=ieY(ω),(11а)

ук ( 0 £ 0)   Yk £toS eUe

φ0=ϕ0-u0=-u(0) ,(12а)

ε 2 ε

φ1=-1D0=-i1U Y(ω).(13а)

εεω S

Учитывая (6) и (10а)–(13а), решим систему (27), (29):

eU ε ( k γ (cos kl - 1) - iZ_a ω sin kl )

-2e2kγ+kγ(2e2+ilZaεω)coskl+(k2lγ2ε-ie2Zaω)sinkl, kSγε2ω(Zaωcoskl - ikγsinkl) -2e2kγ+kγ(2e2+ilZaεω)coskl+(k2lγ2ε-ie2Zaω)sinkl.

Таким образом, матричное уравнение (26) с граничными условиями (25) позволяет найти недостающие значения начального смещения u (0) и адмитанса пластины Y ( ω ) в виде (31), (32), а затем с помощью уравнений (2), (6)–(8) и коэффициентов (10а)–(13а) найти далее все искомые величины при произвольных значениях x ∈ [0, l ] .

Отметим, что вычисление входного импеданса многослойной камеры, рассмотренной в [1], позволяет определять резонансные частоты системы вибратор—камера, если в (24) в качестве волнового сопротивления акустической нагрузки Za принять входной импеданс камеры Zвх . Тогда очевидно, что выражение (32) для адмитанса может быть использовано для определения резонансных и антирезонансных частот согласно изложенной в [2, 8] методике. При Za ≡ 0 (32) опишет адмитанс пьезопластины со свободными границами ikSγε2ωsin kl

(32а)

педанса плоской пластины со свободными границами, совершающей продольные колебания, где однако принята несколько иная скорость звука в пластине.

Отметим, что нерассмотренный здесь случай количества электродов больше двух также может быть принципиально учтен [5 и др.].

ОПРЕДЕЛЕНИЕ РЕЗОНАНСНЫХ ЧАСТОТ

Выше отмечалось, что резонансные частоты могут быть получены из выражения (32), однако приведем более прозрачные, идеологически примыкающие к работе [1] методы.

Пусть правый электрод при x = l граничит с жидким полупространством плотностью ρ ₁ и скоростью звука c ₁ ( ρ ₁ , c ₁ — характеристики слоя жидкости, примыкающего к пластине). Граничные условия при x = l требуют непрерывности напряжения T и смещения u :

T_{x = l -}= T_{x = l +}=- P ( l ),                 (33)

u_{x = l -}= u_{x = l +} .                              (34)

В краевом условии (33) учтена противоположность знаков напряжения и давления в жидкости.

В установившемся режиме амплитуда колебательной скорости с учетом временнóй зависимо- сти e imt равна

V ( x ) = - imu ( x )

и связана с давлением в жидкости известным соотношением

V ( x )=— dM . imp 1 d x

Объединяя (35) и (36), имеем окончательно для краевого условия (34):

,         1 dP u _, =---     •

=^- юр i a x x =, ₊

Давление в жидкости будем искать в виде

P ( x ) = A cos k₁ x + B₁ sin k₁ x ,

где k₁ = m / c₁ — волновое число жидкости. Неопределенные коэффициенты A ₁ и B ₁ находятся из условий (33), (37).

Таким образом, получены все выражения для расчета акустических волн в системе пьезоизлуча-тель—жидкое полупространство .

Перейдем теперь к определению резонансных частот реальной многослойной ультразвуковой камеры, разобранной в работе [1] и облучаемой рассмотренным пьезоэлектрическим излучателем. Напомним, что ультразвуковая камера состоит из N жидких слоев, сопряженных справа с однородным жидким полупространством. Для определения резонансных частот необходимо воспользоваться одним из предложенных в [1] методов.

Метод вронскиана

В этом случае строятся два решения y _1,2( x ), удовлетворяющие соответственно левому и правому краевым условиям. В качестве решения y ₁ ( x ) берется решение (38) в любой точке x , расположенной в первом водном слое, примыкающем к излучателю и имеющем акустические параметры ρ ₁ , c ₁ . В качестве решения y ₂ ( x ) берется решение, удовлетворяющее правому граничному условию в резонансной камере (см. [1]). После этого рассчитываются резонансные частоты ω как суть решения задачи:

| w ( m l )| = miin | w ( m )| =

= min I y i ( x , m ) y x 2 ( x , m ) - y xi ( x , m ) y 2 ( x , m )| •     ⁽3⁹⁾

ω

Метод дисперсионного соотношения

Согласно [1], резонансные частоты соответствуют решениям дисперсионного соотношения arg(V-(x, f )V+ (x, f)) = 2mn,       m = 0,1,2,... (40)

где x — некоторая точка, в частности, в первом жидком слое. Примем x = l (поверхность вибратора). Тогда V - ( I , f ) — коэффициент отражения плоской волны, падающей справа налево на вибратор из однородного полупространства x е [ I , да ) с акустическими характеристиками примыкающего к поршню слоя; V ₊ ( I , f ) — коэффициент отражения плоской волны, падающей слева направо из однородного полупространства а е ( -да , I ] с акустическими характеристиками примыкающего к поршню слоя на систему слои—примыкающее к ним однородное полупространство .

Здесь, однако, оба этих метода использоваться не будут, а будет рассматриваться частотное поведение адмитанса, а также значений напряжения T ( l ) и смещения u ( l ) на границе с жидкостью.

Таким образом, получены все выражения для вычисления резонансных частот резонаторной ультразвуковой камеры, состоящей из пьезоэлектрического вибратора и системы слоев, сопряженных с однородным полупространством.

Табл. 1. Характеристики резонаторной камеры

№ слоя	Ск. звука, м/с	Плотность, кг/м3	Толщина слоя, м
1	1500	1000	5 10–3
2	5570	2600	1 10–4
3	1500	1000	3 10–4
4	5570	2600	1 10–4
5	1500 (330)	1000 (1.3)	да

Табл. 2. Характеристики пьезоэлектрического вибратора

Параметры	Данные
Материал	Sonox P4
Толщина, м	1.01 10–3
Плотность ρ , кг/м3	7800
Скорость звука c , м/с	4460
Диэлектрическая постоянная ε , Ф/м	6.02 10–9
Упругая жесткость (модуль упругости) c % , н/м2	11.6 1010
Пьезоэлектрическая постоянная e , к/м2	15.3

ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

Для иллюстрации полученных выражений был проведен численный эксперимент. Характеристики резонаторной камеры представлены в табл. 1. В качестве полупространства (слой № 5) принимался воздух либо вода. В табл. 2 приведены характеристики пьезоэлектрического вибратора. Данные заимствованы из работы [3].

Отметим, что скорость звука (продольная) в пьезопластинке в данном случае рассчитывается по формуле (6а). Вначале были рассчитаны точки резонанса некоторых характеристик пьезопластин с параметрами, указанными в табл. 2. Результаты представлены в табл. 3. Для сравнения в первой строке таблицы приведены резонансные частоты в пластине с параметрами из табл. 2, но при е = 0 (без пьезоэффекта). Во второй строке представлены резонансные частоты пластины без нагрузки, в последующих строках приведены резонансные частоты адмитанса, а также напряжения и смещения на границе x = l с нагрузкой. Сравнение первых двух строк подтверждает известные факты о том, что, во-первых, пьезоэффект понижает частоту резонанса, а во-вторых, наличие пьезоэффекта устраняет четные гармоники. Анализ строк 2, 3 также подтверждает известный факт понижения частоты резонанса при наличии нагрузки, однако частоты резонанса напряжения T(l) и смещения u(l) при наличии нагрузки остаются практически неизменными и совпадают с частотами без нагрузки.

Табл. 3. Точки резонанса

№ п/п	Резонанс	Первая гармоника, МГц	Вторая гармоника, МГц	Третья гармоника, МГц
1	Пластина без пьезоэффекта, напряжение T ( l )	2.208	4.416	6.624
2	Пьезопластина без нагрузки, Za = 0 , адмитанс Y ( f )	1.957	—	6.548
3	Пьезопластина с нагрузкой Za = z 1 , адмитанс Y ( f)	1.953	—	6.537
4	Упругое напряжение T ( l )	1.957	—	6.548
5	Смещение u ( l )	1.957	—	6.548

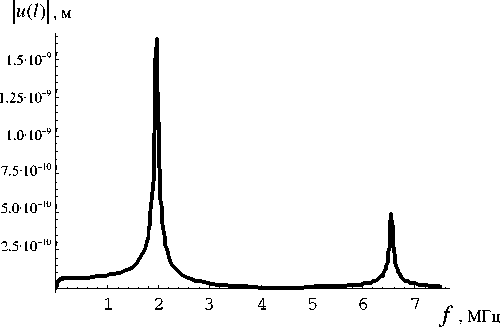
Рис. 1. Резонансная кривая модуля смещения нагруженной пластины, Z_a = z 1 .

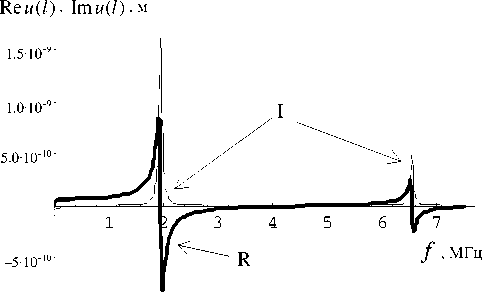
Рис. 2. Резонансная кривая действительной (R) и мнимой (I) составляющих смещения нагруженной пласти ны, Za = z1

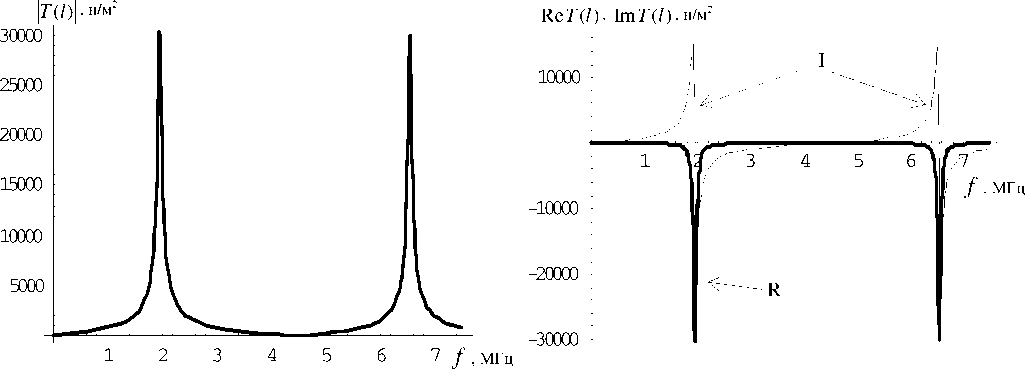
Рис. 3. Резонансная кривая модуля напряжения нагруженной пластины, _a z ₁

Рис. 4. Резонансная кривая действительной (R) и мнимой (I) составляющих напряжения нагруженной пластины, Z_a = z ₁

1.5

0.5

-0.5

-1

-1.5

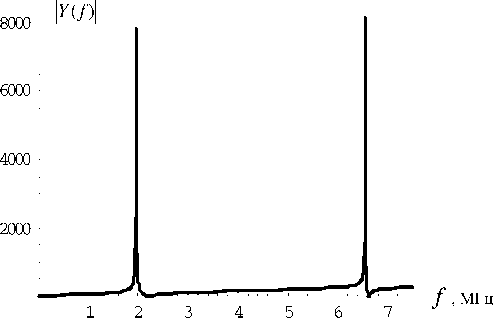
Рис. 5. Резонансная кривая модуля адмитанса ненагруженной пластины, Z_a = 0

Arg Y ( f )

f , МГц

Рис. 6. Резонансная кривая аргумента адмитанса нена-груженной пластины, Z_a = 0

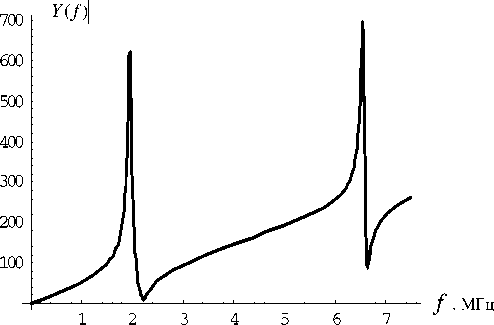
Рис. 7. Резонансная кривая модуля напряжения нагруженной пластины, a z 1

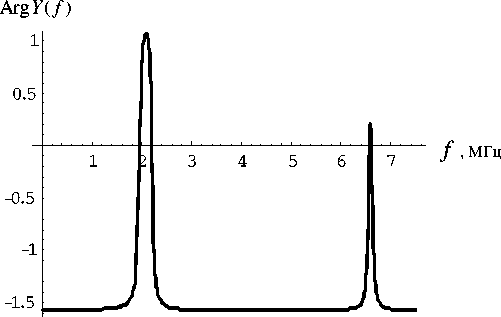
Рис. 8. Резонансная кривая аргумента адмитанса нагруженной пластины, Z = z

На рис. 1–4 приведены резонансные кривые модулей и реальных и мнимых составляющих смещения u ( l ) и напряжения T ( l ) пластины с нагрузкой. Видно, что на резонансе реальная составляющая смещения и мнимая составляющая напряжения равны нулю, в то время как другая составляющая принимает максимальное значение.

На рисунках 5–8 приведены резонансные кривые для модуля и фазы импеданса ненагруженной и нагруженной на Z_a = z ₁ пластины. Видно, что нагрузка на порядок уменьшает модуль импеданса и размывает фазовую кривую.

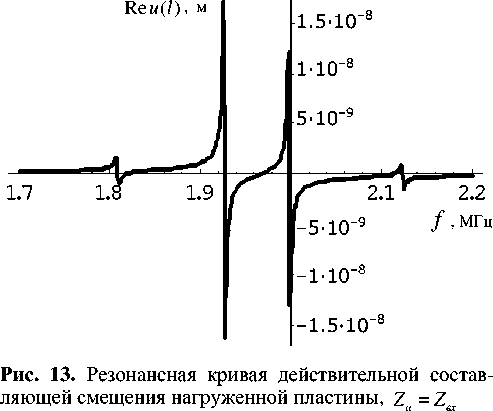
Далее были произведены расчеты при Za = Zвх для резонатора с жидким полупространством (см. табл. 1). Результаты приведены на рис. 9–15. На рис. 10, 12 и 14 представлены соответственно те же зависимости и в том же диапазоне, что и на рис. 3, 7 и 1 для случая постоянного импеданса на- грузки Za = z1 . Видно, что при частотно зависимом импедансе появляется целое множество резонансных максимумов, обусловленных этой зависимостью. Наиболее значимые из этих максимумов по-прежнему концентрируются в окрестностях собственных частот пластины. Более детально резонансные кривые представлены для реальных и мнимых составляющих напряжения и смещения на границе с жидкостью соответственно на рис. 9, 11 и 13, 14. По ним, а также по резонансной кривой для модуля адмитанса были просчитаны значения резонансных частот для двух наиболее значимых максимумов в окрестностях первого резонанса ненагруженной пластины f1 = 1.957 МГц (см. табл. 3). Расчеты по всем трем кривым дали идентичный результат (округление с точностью до сотен Гц): f = 1.927 МГц и f = 1.999 МГц.

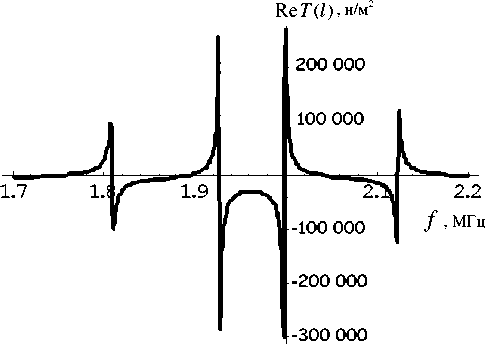
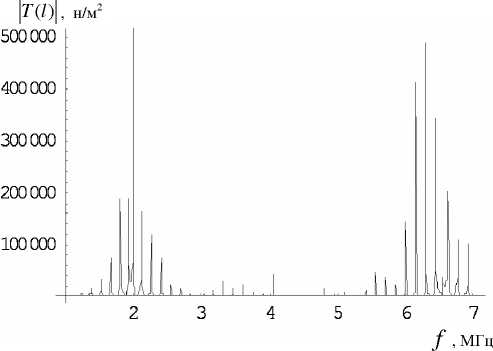
Рис. 9. Резонансная кривая действительной составляю- Рис. 10. Резонансная кривая модуля напряжения на-щей напряжения нагруженной пластины, Z = Z_вх       груженной пластины, Z_a = Z_вх

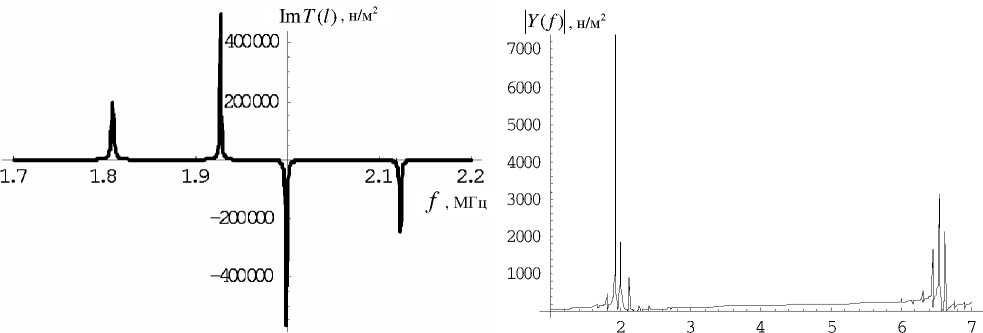
Рис. 11. Резонансная кривая мнимой составляющей                                            f , МГц напряжения нагруженной пластины, Za = Zвх           Рис. 12. Резонансная кривая модуля адмитанса нагру

женной пластины, a вх

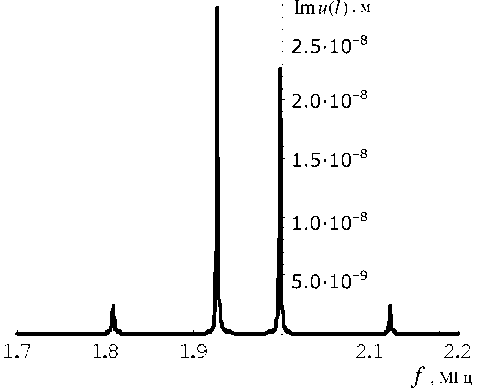
Рис. 15. Резонансная кривая мнимой составляющей смещения нагруженной пластины, Z_a = Z _вх .

u ( l ) , м 2·10^–8

1.5·10–8

1·10–8

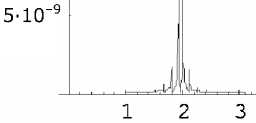
Рис. 14. Резонансная кривая модуля смещения нагруженной пластины, a вх

i—l___I____I____I___и___I____I___I____I____I__ iH UI W/V* *1 iH___

4    5     6     7

f , МГц

При этом очевидно, что экстремумы на кривых соответствуют именно резонансным, а не антире-зонансным частотам, т. к. в этом случае максимальны значения амплитуд смещения и напряжения на границе с жидкостью, что максимизирует проходящую в резонатор энергию. Отметим также, что на резонансах реальные и мнимые составляющие напряжения и смещения на границе с жидкостью ведут себя "резонансным" образом. А именно, если одна составляющая равна нулю, то вторая принимает экстремальное значение.

Аналогичные расчеты были произведены для случая, когда полупространством является воздух (см. табл. 1, слой № 5). Качественно характер зависимостей остается тем же, что и для водного полупространства. Однако значения рассмотренных функций растут на 4–5 порядков в окрестностях резонансов, что является следствием более высокой добротности в этом случае. Кроме того, значения резонансных частот для воздушного полупространства увеличиваются на величину порядка 300 Гц, что также является естественным (см. [1]).

ВЫВОДЫ

Таким образом, в работе предложен подход, позволяющий рассчитывать характеристики ультразвуковых резонансных камер, состоящих из пьезоэлектрического излучателя и многослойной жидкой камеры, граничащей в общем случае с жидким полупространством. Предложенный подход позволяет получить исчерпывающую информацию о физических процессах в камере.

Работа выполнена при поддержке фонда РФФИ, грант № 05-03-33108.