Расчет силы давления непараксиального гауссова пучка на однородный цилиндр с круглым сечением

Дифракция электромагнитной волны на однородной сфере может быть проанализирована в рамках теории Ми. Обобщение теории Лоренца - Ми на случай дифракции гауссова пучка и пучка произвольной формы рассмотрено в [1-3] и [4] соответственно. Строгий электромагнитный расчет силы давления на сферическую микрочастицу со стороны гауссова пучка с непараксиальностью 5-го порядка рассмотрен в [3, 5, 6]. При этом гауссовый пучок имел радиус перетяжки много больше, чем длина волны света. Более «острую» фокусировку гауссова пучка можно осуществить с помощью сферической линзы с высокой числовой апертурой, обладающей аберрациями. Расчету сил давления света на сферическую частицу, расположенную в фокусе линзы с аберрациями, посвящены работы [7, 8]. Однако расчет в [7, 8] был осуществлен для рэлеевских частиц, то есть с использованием теории рассеяния 2-го порядка. В [9, 10] рассмотрен строгий расчет сил, действующих на сферическую частицу произвольного радиуса, расположенную в фокусе сходящегося пучка со сферической аберрацией. Однако действие силы давления света рассмотрено только вдоль оптической оси. В [11, 12] проведено моделирование и строго рассчитаны силы, действующие на сферическую частицу, расположенную в фокусе сходящейся сферической волн. В [13, 14] приведено теоретическое и численное сравнение 3-х методов расчета силы давления света: геометрооптического, в приближении Рэлея и строгого. Аналитические выражения для силы давления света на сферическую частицу с керровской нелинейностью, расположенную в фокусе гауссова пучка, получены в [15]. В [16] рассмотрена передача углового момента от плоской электромагнитной волны с круговой поляризацией сферической частице. В [17, 18] приведены аналитические формулы для расчета полей дифракции непараксиального 2D гауссова пучка на круглый диэлектрический цилиндр.

В данной работе приведены аналитические выражения, и проведено численное моделирование для расчета сил давления света на диэлектрический цилиндр с круглым сечением, расположенный вблизи фокуса двумерного непараксиального гауссова пучка.

1. Сила давления света на микрообъект

В [19] приведена формула, выражающая сохранения полного импульса системы электромагнитного поля плюс объект V , ограниченный поверхностью S :

I; J P i dV + "1; P 0i = - f ^ст ik n k dS, о t •           d t •

V ₁                           S ₁

где P i – координаты вектора импульса электромагнитного поля ( V ₁ и S ₁ – объем и ограничивающая его поверхность, который включает объект V е V 1 ), связанного с вектором Умова-Пойнтинга соотношением:

P = S = У"" [ E ^х H ] ,(2)

c2   4п c дPm

P – координаты вектора импульса объекта,   0i – д t координаты вектора силы давления света на объект;

Г

_ 1

"k 4п

E ² +1 H I²

\

-8 1 E i E k - H i H k ) ;

стik - максвелловский тензор напряжений электро магнитного поля (стik = стki); E , H - векторы напряженностей электрического и магнитных полей в вакууме, 81 - диэлектрическая проницаемость среды.

После усреднения по времени за период 2 п

T = — монохроматического света: ю

E(X,t) = Re { E(x)e i ^ю t } ,

H(X,t) = Re {H(x)e‘ю t} вместо уравнения (1) получим:

Fi=\"P0L/ = 4^k)nkdS,(5)

\ dt так как

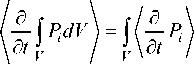
Для получения выражения для усредненного по времени тензора напряжений (3) учтем, что

R Re ECx )e ^m t ) Re ( E j (x )e^im t ^ =

= 2 Re Ei_t(x)E*(x) ] .                          (7)

Тогда, вместо (5), получим:

F x = 8 П S { 1 ^s 1 E x^ ^{2 +} H ^{2 -S 1}I E y\ ^{2 -}

- H y P -S1| E z P — H z |² ] dS x +

+ Re ( s, E_rE * + hH * W + 1 xy x y y

+ Re ( si E x E + H x H * ) dS z } ,

F = £ f | ¹ [= 11 E y 2 ⁺ H y । "S il E x\ ’ - n s

- | H x |² "=i | E z |² "  H z I² ] dS y +

+ Re ( s. EE * + H H * W + yz    y z z

+ Re (s, EE* + HH*) dS}, yx    y x    x

^F * = i f | 1 [ = i H + HA² -= il EA² -

O U _S I 2

- H x |² -=1| E y |² - H y |²] dS *

+ Re (s, E.E * + HH * W + zx zx x

+ Re (si EE + EH) dSy},(O)

dzd где dSx =--dxdy, dS = —dxdy, dS = dxdy, dx           y dy

E 1 = E_x , E ₂ = E y , E 3 = E_z (для H i и F i аналогично).

Перепишем выражения (8) для силы давления света на микрообъект в 2D случае в системе СИ. Для ТЕ-поляризации (Hx = Ey = Ez = 0) электриче ское поле направлено вдоль оси X: Ex ^ 0 , Z - оптическая ось, 2D-объект имеет вид цилиндра с произвольной формой сечения и имеет бесконечную протяженность вдоль оси X. Плоскость YOZ – плоскость падения света. В этом случае соотношение (8) примет вид:

Fx = 0 x

F y = 1 s o f l у ^[ H y |² -sil E x\ ²-I H z\² 1 ds , +

2 S112 LJ

+ Re (HyH*)dSz},(9)

^Fz = ^{1 s} ° f {^{1 [} H z |^{2 -s}1| E x l^{2 -} | ^Hy |² ] ^dSz +

S 1

+ Re (HzH* )dSy},(10)

здесь S ₁ уже контур, охватывающий сечение объекта в плоскости YOZ . Сила F_z – направлена вдоль оптической оси и является аналогом рассеивающей силы для рэлеевских частиц [7], а F_y - направлена поперек оптической оси и является аналогом градиентной силы [7].

Связь между проекциями H_y , H_z и E_x следует из уравнений Максвелла:

-

H y

i dE         i dE xx

--, H z =--, k d z        k d y

где k = — - волновое число света с длиной волны

X

X . Аналогично (9) и (10) сила давления света с ТМ-поляризацией на 2D объект будет иметь следующие проекции ( E_x = H y = H_z = 0):

F x = 0

{ 1 Г I |2         ,       , 2     ,       , 2

"2" ^s 1 | ^Ey | ^-s 1| ^Ez | ^- l ^Hx| ^dSy ⁺

F y = ^{1 s} 0 f

² S 1

+ Re ( s i E y E * ) dS z } ,

F z = ^{1 s} 0 f ^{1 1 [s} 1 ^Ez\^{1 -s} 1| ^Ey |^{2 -} H x l² ] ^dSz ⁺ S 1

+ Re ( s i E z E * ) dS y } ,                             (12)

где (как и в уравнениях (9) и (10)) dS y = n y dl = sin ф dl = dz и dS_z = n_zdl = cos ф dl = dy , dl – элемент дуги контура S ₁ .

2. Дифракция непараксиального гауссова пучка на 2D круглом однородном цилиндре

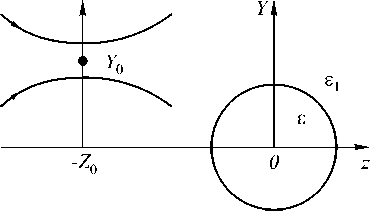
Рис. 1. Схема падения гауссова пучка с фокусом в точке (- Z0 , Y0 ) на круглый цилиндр с центром в точке (0;0)

Следуя [18], рассмотрим дифракцию 2D непараксиального гауссова пучка на круглом однородном цилиндре (рис. 1). Для случая ТЕ-поляризации, когда (Ex, Hy, Hz) – отличны от нуля, напряженность электрического поля для непараксиального гауссова пучка можно записать в виде:

E x ( P - ф ) =

^E O ® oV ⁿ X

to

J ^exp

-to

k ² ю 0 q ² 4

+ ik ( z 0 p - y 0 q ) + ikr cos ( ф - у )] dq ;

где y = arcsinq , p + q = 1, p = cos у , q = sin у .

Так как:

to

Ex = Eо Zi 1 H )(kr)einф, n=-to exp[ikrcos(ф-у)] = ZinJn(kr)e‘n(ф Y),      (14)

n = -to то получим разложение (13) в ряд по цилиндрическим гармоникам:

to j Hф = iH0 ZinCH(1 )(kr)eф,

^Hr ^S

to

= Hо Z ninC n=-to

S H n ^{( 1 )} (kr) n     _kr

e^{in ф}

to

Ex(P,ф)= Eо ZinCnJn(kr)enф , n = -to

C n

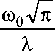
to

J exp

-to

k ² ® 0 q ²

Ek где H 1 = 0 1 , k1 = kve , б - диэлектрическая про-цю ницаемость цилиндра. Граничные условия непрерывности тангенциальных составляющих поля на границе цилиндра имеют вид:

+ ik 1 - - q ² z 0 - ikqy 0 - inarcsinq dq .         (16)

Из уравнений Максвелла можно далее рассчитать напряженности магнитного поля:

E x + E x - E m = 0 , h ф + h ф - h m = 0 .

/■ =-

^H z =

i dEx , юц dz i dEx юц dy

Перейдем к проекциям поля в полярных координатах:

H r = H_z cos ф + H y sin ф , ^H ф = ^- H sin Ф + H y cos Ф ..

Тогда для проекций магнитного поля получим:

H ф (г, ф ) = iH о Z i n C n J' n (kr)e^{in ф} ,            (19)

n=-to где

J‘(kr) = ~^—J„(kr) , n        d( kr ) n kE0

H 0 =     , цю

H r (r, ф ) = H 0 Z i n nC n J n ikrle n ^ф .         (20)

Аналогично запишем разложения рассеянного

—S —S            —m —m

E , H и внутреннего E , H электромагнитных полей по цилиндрическим функциям:

Подставляя в (23) выражение для полей (21), (22), а также (15), (19) и (20), получим систему для двух неизвестных из двух уравнений, из которой следует выражения для коэффициентов разложения в рядах (21) и (22):

C n ^S = a n C n , C n “= b n C n ,                      (24)

a n = ( k 1 J n (k 1 R)J n (kR) - kJ n (k 1 RJ n (kR) ) / / ( k 1 J n (k 1 R)H ^) (kR) - kJ n (k 1 R)H n( ¹ ) (kR) ) , (25) b n = ( ldn(kR)H'_n^{( 1} ) (kR) - kJ n (kR)H n1 ) (kR) ) / / ( k 1 J n (k 1 R^H n ¹ ) (kR) - kJ n (k 1 R)H n( ¹ ) (kR) ) . (26) Так как в уравнениях (25) и (26) цилиндрические функции входят в выражения в виде произведения, то a - _n = a_n и b - _n = b_n . В выражения для силы (9) и (10) входят проекции поля в декартовых координатах. Мы же получили решения для полей в полярных координатах (15), (19), (20) - (22).

Поэтому перейдем от поля в полярных координатах к полю в декартовых координатах:

[          E x = E x ,

< H_z = H r cos ф - H _ф sin ф , .                  (27)

[ H y = - H r sin ф + H _ф cos ф.

Тогда:

^Hz^(r > ф ) =

E x’ = E 0 Z i n C m J n (k 1 r)e n ^ф , n =to^to

m = iH 1 Z i n C n m J n (k 1 r)e^{n ф} ,              (21)

n =-to

H_r^m = H 1 Z nine J^{n(k 1 r)} e^{in ф} , n =-to             ^k 1 ^r

= H 0 Z iⁿC n e^{in ф} j ncos ^ [ J n (kr) + a n H n ¹ ) (kr) ] -

- isin ф [ J n (kr) + a n H n ¹ ) (kr) ]} ,                 (28)

H y = H 0 Z i n C n e n 4 nsin ^ - [ J n (kr) + a n H n¹ ) (kr) ] + n            I kr

+ ^icos ф ^[ J n^(kr) + a n H n ^{( 1 )}(kr) J) ,                (29)

E x (r, ф ) = E о £ i n C n e n ^ф

■\jn(kr) + anH(' )(kr) ].(30)

Для компактности введем функции:

фS = Jn(kr) + anHn1 )(kr),(31)

ф n = Jn (kr) + a H . kr) v'.(32)

Тогда перепишем (28-30):

^Hz^(r , ф ) = H о ■

■ £ i n C n e in ^ф | ncos ^{ф ф} n^(r) - isin ф ■ ^n (r) | n I kr

^Ну (г, Ф ) = ^H 0 ■

■ £ e n C n e i ^ф | nsk- . ^ф n (r) + isin ф-о-оч j    ( )

E x (r, ф ) = E о £ i n C n e in ^ф ф n (r)

где an – находится из (25), но с учетом замены k на k 4s, а Cn - из (16), но с учетом замены Cn = г nCn,

£ 1 - диэлектрическая проницаемость среды. Подставив (35) в (34), получим:

F r = ^{— £} £ C n l²

⁴ n =-^

H 0² n ²

⁽ k 47 ^— ) 2

^£ 1 E (2

|ф n (—) ² -

- h 0 ²| ф п (— ) ²},

F ф = ^{— i} ° ^H 2- ££ nC n Im [ ф n (— ;Ф' * (—) ] , ²    n =-^

где Im [. .. ] - мнимая часть числа, а вместо (31) и (32) используем обозначения:

^ф n⁽r) = a n H n 1 ) ( ^k 77 r ⁾⁺ J n ( ^k 77r ) ,

^ n (r) = a n H n ⁽ 1 ) ( k 77r ) + J n ( k 471r ) ,         (37)

Подставив (33) в (27), можно получить аналитическое выражение для проекций силы, действующей на круглый однородный цилиндр, расположенный вблизи перетяжки непараксиального гауссова пучка. Для круглой частицы аналитическое выражение получено в [15].

Чтобы получить аналитическое выражение для силы давления света на диэлектрический цилиндр с круглым сечением, удобно использовать выражения в полярной (цилиндрической) системе координат.

Тогда, вместо (9) и (10), будем иметь:

J n (x) = dJTxl dx

.

В системе СИ H ₀ = E ₀ 4£i ( Ц = 1 )•

Так как выражение (36) должно выполняться при любом радиусе окружности — >  — ₀, по которой происходит суммирование в (34), R ₀ – радиус круглого сечения диэлектрического цилиндра, то (36) должно выполняться и при — ^ » .

Тогда первое уравнение в (36) можно переписать ( ц = 1):

2nr

F r = -7° 1 H - P — H .1 -' 11 E x l¹ d ф •

F r =

”

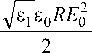
£ Cn|2- n = -^

F » = ^—' _л 1 -e ( H r H ф d ф ,

■ ( ф n (—)² +7n (—)\² ) •

где проекции векторов напряженности электрического и магнитного полей для TE-поляризации H_r , H _ф и E x вычисляются по формулам (15), (19), (20) и (22) для - >  - 0 , если — ₀ - радиус круглого цилиндра:

E x = E 0 £ C n [ a n H n ¹ ) (k47r) + J n (k47r)e n ^ф , n =-^

Далее перепишем (38), с помощью использования асимптотик для цилиндрических функций, при x ^ « :

^Jn^(x) =

-

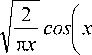
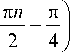
и ( 2 ) / 1 j ²          7    ^П n

^Hn ^{) (x)} = J exp exp ^- i l x ^--—

V n x    L V 4

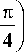
H r = H 0 £ - C T n [ a n H n ¹ ) (k.£r) + n =-rc k V' ^r

а также используя рекуррентные соотношения для Z цилиндрических функций

⁺ J n

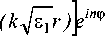
z n (x) = -Z n (x ; - Z n + 1 (x) .

x

Тогда, вместо (38), получим, что:

H ф = H 0 £ C n [ a n H n ^{( 1} ) (k^r) + n =-^

+ J n (k 47r) e ‘ ^{n ф} ,

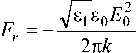
■ £ C n |^{2 (} 2| a n |^{2 + 2}| ^an\^cos(ar g ^an ) ⁺ 1 ) ,           ⁽⁴¹⁾

n =-№ где arg an – аргумент комплексного числа an .

Проекция силы на радиальную координату F_r по сути является модулем вектора силы, то есть:

F r = V F y + F z .

Поэтому уравнение (41) дает только величину силы, а ее направление остается неизвестным. Найдем по отдельности проекции силы на оси Y и Z из уравнений (9) и (10) с учетом выражения (27). Тогда получим:

2n-

n 2 П

F y =--0- J | H ф| sin З ф ^{+ S} 1 E^ ⁿ Ф d Ф , 4 0 ^{L                            J}

2 n

Fz =- -0- J |H ф| cos 3Ф +

+ S 1 | E_z |² cos ф]^Ф .

Подставив в (42) составляющие поля из (35) в виде рядов по цилиндрическим функциям и устремив R в бесконечность, получим:

F y

^S 0

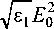
4 n k

to

Z Cnan n=-to

**  **

‘ C n + 1 a n + 1 ⁺ C n - 1 a n - 1

-

****

C n + 3 a n + 3    C n - 3 a n - 3 ) ,

_ i s о 7s 1E02 у        ** _

F z , , Z C n a n ( C n + 1 a n + 1 ^{4 n k}    n =-to

**  ****

• ^- C n - 1 a n - 1 ^- C n + 3 a n + 3 ⁺ C n - 3 a n - 3 ) .

  
  

• 3. Численное моделирование

Удобно объединить обе проекции (43) в одну – вида:

F z + iF y

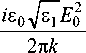
to E*   *      **

Cnan (Cn+1 an +1 - Cn+3an+3 ) .

n =-to

На рис. 2 представлена картина интерференции двух гауссовых пучков, направленных друг против друга с перетяжкой в начале координат, создающих стоячую волну. Рис. 2а отображает амплитуду суммарного поля Ex (TE-поляризация), рис. 2б – модуль проекции вектора Умова-Пойнтинга на ось распространения света Z . Первый гауссовый пучок направлен вдоль оси Z , второй пучок в обратном направлении оси Z . Для первого гауссова пучка длина волны излучения – 1 мкм, мощность излучения – 50 мВт/м, перетяжка гауссова пучка находится в начале координат, ее диаметр – 1 мкм. Мощность излучения второго пучка – 50 мВт/м, длина волны так же равна 1 мкм, а диаметр перетяжки –1,5 мкм. Если поместить в такое поле диэлектрический объект, имеющий размер порядка длины волны, то данное поле окажется для него ловушкой: он будет втягиваться в максимумы интенсивности поля.

На рис. 3 представлен график зависимости силы Fz направленной вдоль оси Z от смещения по оси Z .

Объектом является круглый цилиндр с диаметром равным 1 мкм, диалектрическая проницаемость – s =2. Вся картина дифракции имеет размер 2,5x2,5 мкм.

а)

б)

Рис. 2. Интерференционная картина двух непараксиальных гауссовых пучков, распространяющихся навстречу друг другу вдоль оси Z: а) суммарная амплитуда векторов электрической

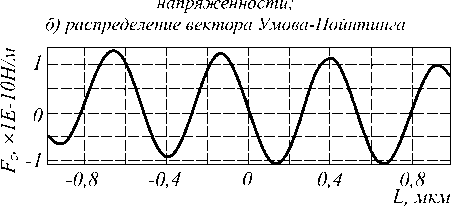
Рис. 3. Проекция на ось Z силы, действующей на круглый цилиндр с S =2 в зависимости от смещения центра круга цилиндра вдоль оси Z

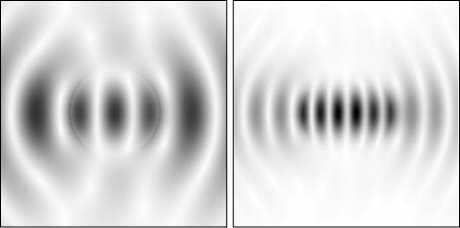
На рис. 4 представлена дифракция направленных друг против друга гауссовых пучков, изображенных на рис. 2, на круглом цилиндре, описанном выше. Рис. 4а представляет напряженность электрического поля Ex (TE-поляризация), рис. 4б – проекцию вектора Умова-Пойнтинга на ось Z . Объект расположен по центру перетяжки ( z =0). Для визуализации на рис. 4а сам объект слегка затемнен.

а)                            б)

Рис. 4. То же, что и на рис. 1, но в присутствии круглого цилиндра в центре перетяжки

На рис. 5 приведена центральная часть картины дифракции рис. 3а размером 0,31x0,31 мкм. Стрелками отображены направления силы, действующей на данный цилиндр со стороны излучения, при помещении объекта в каждую конкретную точку пространства. Можно видеть, что объект хорошо «втя- гивается» в максимумы интерференционной картины. Длина стрелки пропорциональна модулю силы.

Рис. 5. Поле векторов сил, действующих со стороны двух встречных гауссовых пучков на круглый цилиндр, центр которого расположен в разных точках интерференционной картины

Интересно рассчитать поле и силу света, действующую на диэлектрический 2D объект, показатель преломления которого меньше, чем среды.

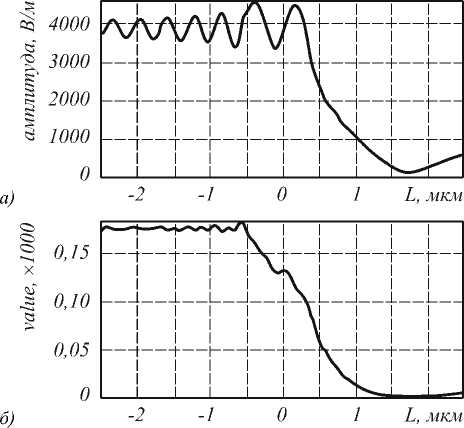
На рис. 6 представлена картина дифракции плоской волны в среде с показателем преломления 1,33 (вода) на круглом цилиндрическом объекте с показателем преломления 1 (цилиндрический пузырек воздуха). Диаметр цилиндра равен длине волны, т.е. – 1 мкм. Рис. 6а представляет напряженность электрического поля Ex (TE-поляризация), рис. 6б – проекцию вектора Умова-Пойнтинга на ось Z . Энергия за «пузырек воздуха» почти не распространяется, что хорошо видно на срезах, отображенных на рис. 7, сделанных по оси Z через точку y=0 .

а)                                   б)

Рис. 6. Модуль напряженности электрического поля (а) и модуль вектора Умова-Пойнтинга (б) на картине дифракции плоской волны на воздушном круглом цилиндре в воде

Рис. 7а отображает значение амплитуды Ex , рис. 7б – значение проекции вектора Умова-Пойнтинга на ось Z .

Если такой объект поместить вблизи фокуса Гауссова пучка, то он будет выталкиваться из него, что проиллюстрировано на графиках рис. 8.

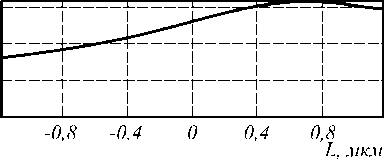
На рис. 8а представлен график зависимости силы Fz вдоль оси Z от смещения по оси Z, на рис. 8б – зависимость силы Fy от смещения вдоль оси Y через фокус. Гауссовый пучок имеет длину волны 1 мкм, диаметр перетяжки равен 1 мкм, мощность излучения 100 мВт/м. Видно, что при отклонении в любую сторону из фокуса в поперечном направлении сила, направленная в сторону отклонения, возрастает, что приводит к устойчивому движению в этом направлении. При отклонении вдоль оси распространения света Z сила, действующая на объект, перед фокусом меньше по модулю, чем после фокуса.

< 1-2

$ 0,8

а)

Рис. 7. Сечения картины 6а и 6б вдоль оси Z через точку Y=0

<‘ О

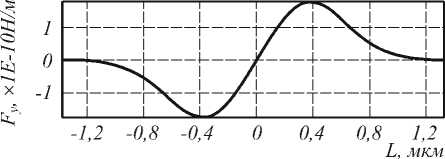
Рис. 8. Проекции силы давления непараксиального гауссова пучка на «цилиндрический пузырек воздуха» в воде: на продольную ось (а) и поперечную ось (б)

Если показатель преломления среды меньше, чем показатель преломления частицы, то при определенных параметрах можно наблюдать «захват» частицы по оси Z .

На рис. 9 показан график силы Fz при захвате вдоль оси Z. Парметры эксперимента: длина волны 1 мкм, диаметр перетяжки Гауссова пучка 1 мкм, диэлектрическая проницаемость частицы 1,2, среды 1, диаметр частицы 2 мкм. Из графика можно видеть механизм захвата: сила Fz перед фокусом положительна и направлена в сторону фокуса, за фокусом отрицательна и толкает частицу назад, в фокус. Из численных экспериментов было определено, что наличие возмож- ности захвата зависит от диэлектрической проницаемости частицы. Для приведенных параметров «захват» имеет место при 1< ε <1,35.

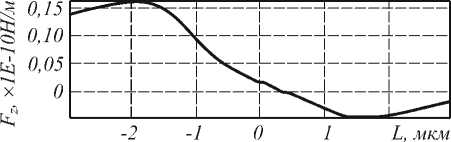
Рис. 9. Проекция силы давления на ось Z для гауссова пучка, действующего на круглый цилиндр с ε =1,2 (среда ε ₁ =1)

График зависимости силы Fz при данных параметрах и диэлектрической проницаемости частицы 1,35 показан на рис. 10.

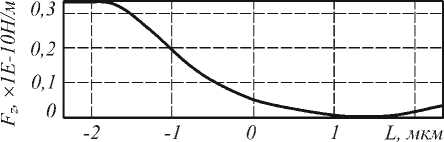
Рис. 10. Граница «захвата»: проекция силы давления на ось Z для непараксиального гауссова пучка и круглого цилиндра с ε =1,35

Заключение

В работе получены следующие результаты:

• •    Получено выражение для силы давления света на диэлектрический бесконечный цилиндр с произвольным сечением в декартовых (ур. (9), (10), (12) и цилиндрических (ур. (34) координатах;

• •    получены выражения для силы давления света (в частности непараксиального гауссова пучка) на диэлектрический бесконечный цилиндр с круглым сечением: при произвольном радиусе окружности интегрирования (ур. (36) и при бесконечном радиусе (ур. (41), (43), (44);

• •    численно показана возможность оптического «захвата» диэлектрического цилиндра с круглым сечением двумя встречными непараксиальными гауссовыми пучками (рис. 3 и 5) и одним гауссовым пучком при ограничении на диэлектрическую проницаемость цилиндра (рис. 9);

• •    численно показано, что круглый «воздушный пузырек» в воде выталкивается из фокальной области непараксиального гауссова пучка (рис. 8).

Работа поддержана российско-американской программой «Фундаментальные исследования и высшее образование» (BRHE), грант CRDF REC-SA-014-02 и президентским грантом НШ-1007.2003.01.