Расчет силы, действующей на сферический микрообъект в гипергеометрических пучках

Уравнение Гельмгольца, которое описывает распространение непараксиальной монохроматической световой волны в однородном пространстве, допускает решения с разделяющимися переменными в 11 различных системах координат [1]. Это означает, что существуют световые поля, распространяющиеся без изменения своей структуры. Примером являются хорошо известные моды Бесселя [2]. Параксиальный аналог уравнения Гельмгольца – это параболическое уравнение типа Шредингера, которое описывает распространение параксиальных световых полей. Это уравнение допускает решения с разделяющимися переменными в 17 системах координат [1]. Световые поля, которые описываются такими решениями, при распространении сохраняют свою структуру с точностью до масштаба. Примером являются хорошо известные моды Эрмита-Гаусса и Лагерра-Гаусса [3].

В работах [4,5] рассмотрено семейство лазерных мод, представляющих собой ортонормированный базис и являющихся решением с разделенными переменными параксиального параболического уравнения в цилиндрической системе координат. В цилиндрической системе координат уравнение Шредингера кроме решений в виде мод Бесселя и мод Лагерра-Гаусса также имеет решения в виде вырожденных гипергеометрических функций. Распределение интенсивности в поперечном сечении таких пучков близко к распределению интенсивности для мод Бесселя. Как и моды Бесселя гипергеометрические моды имеют бесконечную энергию. С помощью дифракционных оптических элементов (ДОЭ) или жидкокристаллических микродисплеев [5], можно сформировать лазерные пучки, близкие к гипергеометрическим модам. В отличие же от мод Бесселя, радиусы световых колец гипергеометрических мод увеличиваются с ростом продольной координаты z как z1/2. В отличии от мод Бесселя семейство гипергеометрических мод двухпараметрическое, что дает возможность регулировать поперечные размеры таких пучков, не меняя порядок фазовой сингулярности. Это свойство может быть полезно в задаче оптического вращения микрообъекта. В работе проведена оценка сил, вращающих сферический микрообъект в гипергеометрических пучках при разных параметрах ДОЭ. Численно показано,

что при сохранении азимутального номера моды и изменении радиального номера моды в несколько раз, сила, действующая на диэлектрический микрошар, диаметр которого меньше ширины яркого светового кольца моды, также изменится примерно в такое же число раз.

1. Теоретические основы

Комплексная амплитуда параксиального светового поля E ( r, ф^ ) в цилиндрической системе координат ( г, ф ,z ) удовлетворяет уравнению типа Шредингера:

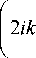
д 1 д д2 дz r д r д r1

1 д ² r ² дф¹

E ( r , ф , z ) = 0,

_ 2п где k = Т" волновое число света с длиной волны

л

X. Уравнению (1) удовлетворяют функции, образующие ортонормированный базис:

E y , n ^{( r} , Ф , ^z )

i n exp Т ⁽ - n

+

n

г I n + 1X i Fl I --------

^{1 1} 1         2

1 I z 0 |2 г I n + 1 + iY | х 2nn!I z J I 2 J

■      a iY ,   z0    ■ iY - 1)+ —ln -°- + in ф

2 z

iY 1-1

—, n + 1, ix I ,

х (2)

где -№ < у < да , n =0, ± 1, ± 2, _ непрерывный и дискретный азимутальный параметры моды (номера моды), от которых зависят функции (2) и которые kw ²

будем называть номерами моды; z ₀ = —2— - ^ана лог длины Релея, w – параметр моды, аналогичный радиусу гауссового пучка, хотя здесь он имеет дру- kr ²

гой смысл; x =----; Г ( x ) - гамма функция;

2 z

₁ F ₁( a,b,x ) – вырожденная или конфлюэнтная гипергеометрическая функция:

₁ F ₁ (a,b, x) =

=      ^Г(Ь)    ) ¹ t a ^{- 1 (} 1 - t^)b - a ^{- 1} e ^xp (xt)dt ’

Г(а)Г(Ь - a) ^J ₀

где Re( b )>Re( a )>0. Из (3) видно, что 1 F 1 ( a,b,x ) – это целая аналитическая функция. В случае (2) Re( x )=0 и тогда уравнение (3) является одномерным преобразованием Фурье от ограниченной функции на отрезке [0,1]. По теореме Шеннона асимптотически при r ^да период модуляции функции (2) (т.е. расстояние между соседними максимумами или минимумами) равно 2 п . При больших значениях аргумента x >>1 имеет место асимптотика

следует, что фаза гипергеометрической функции

равна x /2: arg 1 1 F

n +1 + iy

, n + 1, - ix

x

Интересно, что эта фаза не зависит от номеров моды ( Y n ). Тогда можно записать выражение для фазы ГГ-моды:

Y z ag{ E,n (ГФ z)} =7!n- + пФ+ ,           2z0

kr n      J n + 1 - i Y I

T + (3 n ^{- 1) + ar}gr|—;— 4 z 4             l 2 J ,

n

x ² ₁ F ₁

n + 1 - iy , .

--------------, n + 1, ix

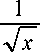
где первое слагаемое имеет смысл фазы Гоу (Gouy).

2. Расчет сил

Поэтому уменьшение модуля функции (2) пропорциональное 1/r при r>>1 происходит быстрее, чем уменьшение амплитуды функции Бесселя (пропорционально 1 r ).

Реализовать световые пучки (2), которые в дальнейшем будем называть гипергеометрическими (ГГ) модами, можно с помощью оптического элемента, имеющего функцию пропускания:

При моделировании формирования ГГ моды использовалось преобразование Френеля:

k . k 1

E ₇ n ^{( Г} Ф, ^z) =7-exP l ⁱ ;7 r I^х

2niz l 2z J

^2n              । k    ।        k f fE,n(P>6)®p| i— P |exp -i-rpcoSO-ф) pdpdO

l 2z J      z

да 2 п

от входной функции E Y , n ^{( p} , ^{6 )} (4).

1 I w I -11 p I, E, n (P6 = —I — I exp iY ln| —1 + in62П ( p J   L V w J

При освещении оптического элемента (4), расположенного в плоскости z =0, неограниченной плоской волной на расстоянии z сформируется световое поле с комплексной амплитудой (2). Энергия световых полей (2) и (4) неограниченна, как и у параксиальной моды Бесселя

Для расчета вращающей силы использовался метод описанный в [6]. Сила рассчитывалась на наиболее ярком кольце ГГ моды, для сферического микрообъекта с диаметром в половину ширины наиболее яркого кольца ГГ моды, по формуле.

Ep , n ⁽ r , Ф , z ) = J n ⁽ P ^{r )ex} P

. в2z^- J i---+ тф ,

2 k

F x = - JJ I ( ^x , y ) ( a x ^- c x ) d^xdy ^c n

F y- = 1 JJ I ^{( x} , y ) ( a y ^- c y ^d^xdy ^c n

где ^в = ^{k sin 6} , 9 - угол наклона конической волны к оси z. Мода Бесселя также удовлетворяет ур. (1). Поэтому на практике для реализации моды (2) оптический элемент (4) следует ограничивать кольцевой диафрагмой. При этом на конечном расстоянии z 0 <  R t^an (у J R ) , где R - больший радиус кольцевой диафрагмы, будет приближенно формироваться мода (2).

Световое поле (2) при распространении сохраняет свою структуру и меняется только масштабно. Поперечное распределение интенсивности ГГ моды (2) представляет собой набор концентрических световых колец, радиусы которых удовлетворяют условию:

где П - область максимального по площади сечения микрочастицы в плоскости перпендикулярной направлению распространения светового пучка, a ^{( a}x , a y , a z ) , b ) ( bx , b y , b z ) , C ⁽ c x , c y , c z )

az^ p = A m^-- pm             ,

V n

где a m - постоянные, зависящие от номера кольца m

и от номеров моды ( Y n ). Из (5) следует, что радиусы колец увеличиваются с ростом z как z ^1/2. Из соотно-

шения [13]:

| n + 1 + Iy

1 Fl Т"

,n + 1, - ix

exp ( - ix) , F 1

n + 1 - Iy

,n + 1, ix

- единичные вектора задают направление падающего и преломленных лучей. Микрочастица размещалась по центру самого яркого кольца, в этом случае возникает сила направленная вдоль кольца F=F x ² +F y² .

При изменении параметра у меняется поперечный размер гипергеометрического пучка. При этом если параметры n и у имеют разные знаки, поперечный размер гипергеометрического пучка уменьшается, как это хорошо видно из рис.1.

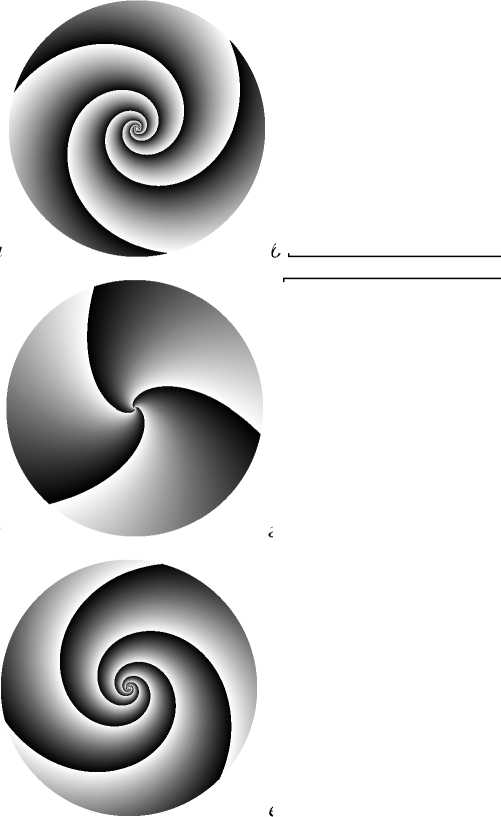
На рис.1 показаны распределения интенсивности различных ГГ-моды с n=3 при различных параметрах у , рассчитанные по формуле (7) на расстоянии z=3500 мм, а также фазы ДОЭ для формирования этих пучков, длина волны 532нм. Размер картин на рис. 1для фазы 5 х 5мм, для интенсивности 1 х 1мм. Число отсчетов - 512 х 512.

Для гипергеометрических мод с параметром n=3, и параметром у который менялся в интервале [-10,10], была рассчитана сила, действующая на микрообъект вдоль светового кольца. Для простоты сила нормировалась на значение силы для у =0. На рис. 2 представлен график зависимости силы F от параметра у .

в

д

Рис. 1.Фазы ДОЭ (а,в,д) и распределения интенсивности (б,г,е) гипергеометрических мод с одинаковым индексом n=3 и параметрами у =-8 (а,б), у =2 (в,г), у =8 (д,е) на расстоянии z=3500 мм.

Как видно из рис.2 при у =-8, сила превышает силу при у =0 (простой оптический вихрь) в четыре раз. И наоборот при у =8 сила меньше, чем сила при y =0 в

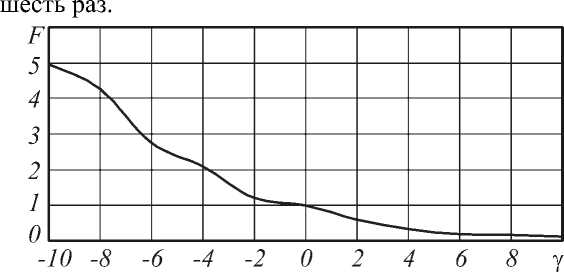
Рис.2 График зависимости силы, действующей на микрообъект в гипергеометрическом пучке с n=3, в зависимости от значения параметра у .

Столь значительное изменение силы очевидно вызвано изменением поперечных размеров пучка. На рис.3 представлен график зависимости радиуса самого яркого кольца ГГ пучка в зависимости от значения параметра y . Радиус определен в безразмерных единицах, где за единицу принят радиус кольца при y =0.

Как видно из рис.3 при y=-8 радиус уменьшается примерно в два с половиной раза по сравнению с радиусом при y=0- Для y=8 радиус увеличивается еще меньше, примерно в 2,2 раза. Т.е. изменение радиуса при изменении y не столь велико, как изменение силы. В чем же причина более быстрого роста силы при увеличении отрицательного Y? Сила действующая на микрообъект должна, очевидно, возрастать пропорционально интенсивности на кольце. А интенсивность на кольце обратно пропорциональна произведению радиуса кольца на его ширину. Из рис.1б, рис.1д, рис.1е можно видеть, что кроме изменения радиуса кольца меняется его ширина. При этом ширина меняется примерно так же как радиус кольца, что хорошо видно из графика зависимости ширины кольца от значения параметра Y, для ГГ пучка с n=3.

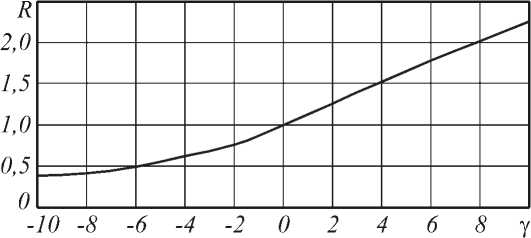
Рис.3 График зависимости радиуса наиболее яркого кольца ГГ пучка с n=3, в зависимости от значения параметра у

Размер микрообъекта при расчете подбирался так, чтобы он целиком размещался внутри самого

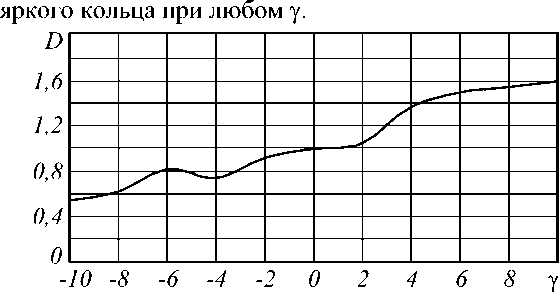
Рис.4 График зависимости ширины наиболее яркого кольца ГГ пучка с n=3, в зависимости от значения параметра у

Однако нельзя бесконечно уменьшать пучок за счет увеличения абсолютного значения отрицательного параметра Y - Начиная с некоторого значения y центральная часть фазового ДОЭ перестает правильно отображаться при заданном разрешении. Так, при размерности 512 x 512 уже при y =20 центральная часть ДОЭ записывается с явными ошибками (рис.5а), при этом в пучке появляются дополнительные кольца по яркости сравнимые с центральным наиболее ярким кольцом.

При этом сила, действующая на микрообъект существенно уменьшилась и составляет всего 1,2 от величины силы при γ=0. Приведенные выше результаты получены для гипергеометрических пучков, распространяющихся в свободном пространстве. При фокусировке этих пучков получить существенное увеличение силы за счет уменьшения диаметра пучка не получается.

а

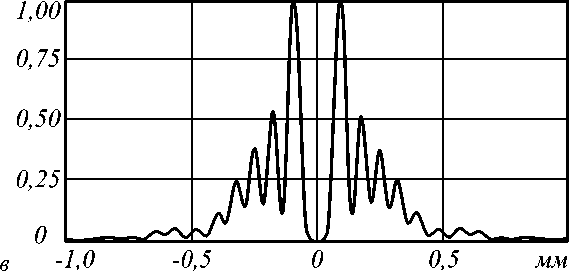
Рис. 5.Фаза ДОЭ (а) и распределение интенсивности (б) ГГмоды с индексом n=3 и параметром у =-20 на расстоянии z=3500 мм, центральное сечение распределения интенсивности (в).

Но в этом случае, тем не менее, удается получить центральное наиболее яркое кольцо меньшего диаметра, чем то же самое кольцо в простом оптическом вихре. Так для оптического вихря с параметром n=1 размер центрального кольца может быть близок к дифракционному пределу, поэтому для задач оптического вращения микрообъектов важно иметь возможность формирования светового кольца меньшего радиуса. На рис. 6 можно видеть, что при фокусировке гипергеометрического пучка с параметром γ=-4 центральное кольцо получившегося пучка имеет диаметр на 20% меньше, чем то же самое кольцо у сфокусированного простого оптического вихря.

Как видно из рис.6а и рис.6б при увеличении модуля отрицательного параметра у происходит уменьшение диаметра центрального кольца. К увеличению вращающей силы это не приводит, т.к. при этом возрастает доля энергии в дополнительных кольцах

Заключение

В работе проведен расчет сил действующих на микрообъекты в гипергеометрических световых пучках. Показано, что использование гипергеометрических пучков с отрицательными значениями параметра у позволяет существенно увеличить силу действующую на микрообъект вдоль светового кольца по сравнению с той же силой, действующей на микрообъект в простых оптических вихрях ( у =0) [7]. Также показана возможность уменьшения поперечных размеров центрального кольца гипергеометрического сфокусированного пучка при отрицательных значениях параметра у .

Работа выполнена при поддержке «Фонда содействия отечественной науке», российско-американской программы «Фундаментальные исследования и высшее образование» (CRDF Project SA-014-02), а также грантов РФФИ 07-07-97600, 08-07-99007.

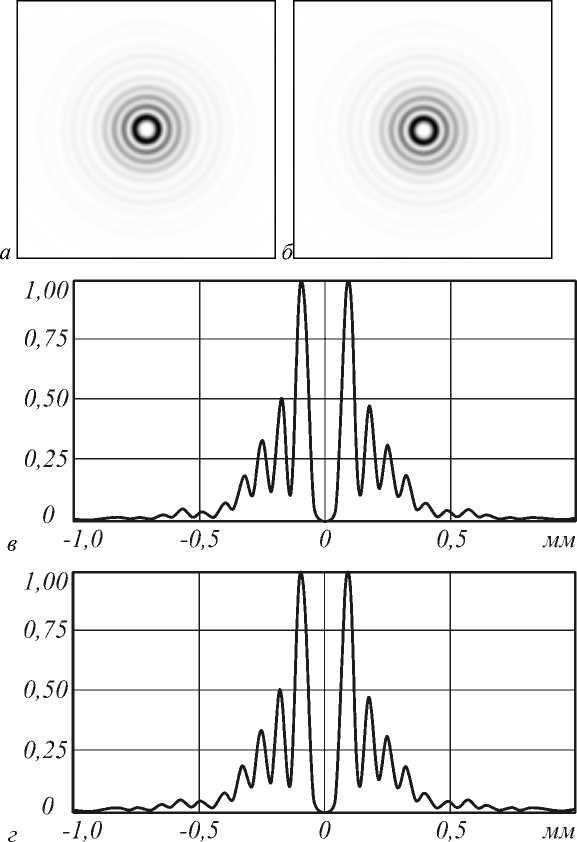
Рис. 6. Сечение распределения интенсивности ГГмоды с индексом n=1 и параметром у =0 в плоскости фокусировки микрообъектива (60 х ) (а), с ечение распределения интенсивности ГГ моды с индексом n=1 и параметром у =-4 в плоскости фокусировки микрообъектива (60 х )(в,г).