Расчет скорости циркуляции жидкости со свободной поверхностью в аппарате с мешалкой
Автор: Газизуллин Назым Абдуллович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Общие проблемы машиностроения
Статья в выпуске: 1-2 т.14, 2012 года.
Бесплатный доступ
С помощью итерационной процедуры на основе алгоритма SIMPLE проведено численное исследование ламинарного течения несжимаемой вязкой жидкости в аппарате с мешалкой. Результаты расчетов представлены в виде линий тока вторичной циркуляции жидкости.
Аппарат с мешалкой, перемешивание жидкости, циркуляция, свободная поверхность, линии тока
Короткий адрес: https://sciup.org/148200596
IDR: 148200596 | УДК: 532.517.2
Текст научной статьи Расчет скорости циркуляции жидкости со свободной поверхностью в аппарате с мешалкой
исключаются, если поверхность воронки располагается выше мешалки. Поэтому расчет формы и глубины воронки представляет несомненный практический интерес. В настоящей работе проведено численное моделирование осесимметричного ламинарного течения несжимаемой вязкой жидкости в аппарате с лопастной мешалкой с учетом образования центральной воронки.
Исходными уравнениями, описывающими течение жидкости в аппарате, будут соответственно уравнения Навье-Стокса и неразрывности в виде [4]
р — + р(— • V)v = -Vp + ^V2 — + pg dt , (1)
V^ v = 0,
где g – ускорение силы тяжести.
Течение жидкости будем рассматривать в неподвижной цилиндрической системе координат r, φ ,z , в которой компоненты вектора скорости обозначим соответственно u, v, w. Данная задача представляет собой задачу со свободной границей. Введем в рассмотрение на поверхности жидкости локальный базис, состоящий из вектора нормали
——
n = <
dh.n .il dr ,0;1 |
и двух векторов в касательной плоскости
— -Ji. dll T1 I1’01 dr [,
T2 = {0; 1’ 0}
где h – высота свободной поверхности жидкости над мешалкой.
Граничные условия на свободной поверхности включают в себя кинематическое и динамическое условия. Кинематическое условие
*
z = 1
d z — Ha — b
dh dr
- w = 0
h
отражает тот факт, что жидкость не может протекать через свободную поверхность и представляет собой равенство нулю проекции вектора скорости на нормаль к поверхности. Динамические условия заключаются в отсутствии трения на поверхности жидкости. На свободной поверхности будет развиваться напряжение p = n • P , которое обусловлено деформацией примыкающих частиц жидкости. Тогда динамические условия запишутся в виде равенства нулю проекций вектора напряжения на направления касательных векторов базиса (4) соответственно как
— *
— * v
v = ^7, nnd
при z < Ha + b при z > Ha + b p. = p - p 0
pfand )2
где n - число оборотов мешалки в единицу времени; H a - высота расположения мешалки над дном аппарата; b - высота лопасти; p0 -атмосферное давление, а в качестве характерной длины и характерной скорости потока выбраны соответственно диаметр мешалки d и окружная скорость конца лопасти nnd . Свободной поверхности жидкости при этом будет соответствовать значение z =1. После преобразования координат уравнение неразрывности (2) сохранит форму
[ П Л 2
dh I А
Т I Prz = 0 dr 7 .
dh
РфZ — Р г ф— = 0 dr
где P - тензор напряжений; pm pzz, prz, Р фz, p^ -компоненты тензора напряжений.
Граничные условия для составляющих скорости на твердых стенках заключаются в отсутствии относительного движения жидкости и твердой поверхности. Тогда на дне и боковой стенке аппарата и=0, v=0, w=0, а на поверхности вала и мешалки соответственно и=0, v=юг, w=0, где ю - угловая скорость вращения вала и мешалки. На оси вращения потока под мешалкой примем и = 0, v = 0,
д w д r
Поскольку форма свободной поверхности жидкости неизвестна и должна быть найдена в результате расчетов, то перейдем от физической области течения к расчетной области с известными границами. Для этого физическую область поделим на две подобласти, нижнюю и верхнюю, горизонтальным сечением, проведенным через верхнюю поверхность мешалки. Введем безразмерные координаты и функции
* *r *
t = nnt, r = —, ф = ф
d
——
v^ V = 0
в которой проекции вектора скорости в расчетной области U, V, W определяются как
* * * * * d Y
U = уи , V = yv , W = w - и z —« dr* , где y =1 для нижней подобласти и Y=h* для верхней подобласти; h =h/d, а и ,v ,w - компоненты вектора скорости в безразмерной физической области, определяемой преобразованием
* r _ _ ** r = -, ф = Ф, dd
В расчетной области уравнение (1) в проекциях на оси координат может быть записано в виде обобщенного уравнения переноса
^^ + — div (V—Ф )= div (ГgradФ )+ 5
д t Y , (8)
где Г =1/( nRe ) - коэффициент диффузии; Re = pnd2/^ - центробежное число Рейнольдса; 5 - член типа источника, соответствующий искомой функции Ф .
Численное моделирование течения проведем методом контрольных объемов [5], одним из основных достоинств которого является то, что он обладает консервативными свойствами, то есть обеспечивает интегральное выполнение законов сохранения для всей расчетной области. Поделим расчетную область на контрольные объемы (ячейки) так, чтобы каждая узловая точка находилась в отдельной ячейке. Грани контрольных объемов расположим посередине между соседними узловыми точками. Размещение всех узловых функций в одних и тех же точках приводит к рассогласованию полей скорости и давления, поэтому выберем разнесенную шахматную сетку [6], в которой точки, где вычисляются компоненты скорости, смещены на полшага в соответствующих направлениях относительно основных точек, в которых вычисляется давление. Проинтегрируем уравнение (8) по контрольному объему и временному интервалу At. Для аппроксимации конвективных членов на гранях ячеек используем схему против потока. В результате с учетом уравнения неразрывности получим дискретный разностный аналог, который связывает значения искомой функции Ф в узловой точке P с ее значениями в центрах Е, W, N, S, T, B соседних ячеек в форме необходимость введения некоторой поправки 5hk к величине h**(k). Эта поправка находилась из соотношения
V - V ( k ) = п ( R 2 - r 2 )^ h ( k )
где R - радиус аппарата; rs - радиус вала; V0 -объем жидкости над диском с невозмущенной свободной поверхностью; V((k - объем жидкости над диском на k-ой итерации, который вычислялся на каждой итерации путем численного интегрирования по значениям h**(k). Следует отметить, что в соответствии с формулой (12) поправка dhPk не влияет на форму свободной поверхности, а лишь корректирует ее по высоте. Окончательно с учетом поправки Shk скорректированные значения формы свободной поверхности могут быть найдены как арфр = аЕФЕ + awФw + а.Ф. + а.Ф. +
h *( k ) = h k ) + 3 h ( k )
г
+ атф + а„ф + AV S
TT BB
P
+ф )
v
At )
Здесь S P - узловое значение источникового члена; Ф0 - значение Ф в момент времени t * ; AV - объем ячейки).
Для расчета формы свободной поверхности жидкости используем формулу пьезометрического напора, которую представим в виде
( k ) _ ( k - i)
h ( k ) = h ( k - 1) + pi-----p i----
P g , (10)
где hik) и hik-1) - значения высоты свободной поверхности над мешалкой на двух последовательных итерациях; pik) и pik ' - соответствующие значения давления на свободной поверхности; i - индекс нумерации узлов в радиальном направлении. Таким образом, предполагается, что изменение давления на свободной поверхности за промежуток времени At вызывает соответствующее изменение высоты свободной поверхности.
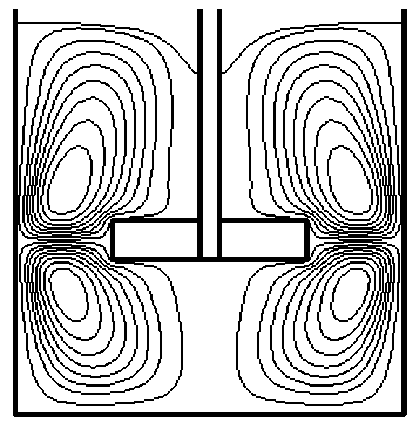
В расчетной области формула (10) примет вид h,"'k1 = h,-(k-1) + п2Fr[p* где Fr=n2d/g - центробежное число Фруда. Очевидно, что рассчитанные по формуле (11) значения h**(k) могут не удовлетворять условию постоянства объема жидкости в аппарате. При этом достаточно учитывать объем жидкости над мешалкой. Таким образом, возникает Расчет поля течения проводился на основе алгоритма SIMPLE [5], в котором используется дискретизация уравнений по методу контрольных объемов на сетках с расположением узлов в шахматном порядке. Граничные условия на свободной поверхности (6), (7) и (5) использовались соответственно при расчете компонент скорости u , v, w из уравнений (9). Форма свободной поверхности жидкости, соответствующая рассчитанному полю течения определялась по соотношениям (11)-(13) в конце каждой итерации. При этом в качестве начальных значений h*(0)принималось значение, соответствующее положению невозмущенной поверхности жидкости. Дискретные уравнения (9) решались методом прогонки [7] в радиальном направлении. В качестве критерия сходимости рассматривалась сумма модулей невязок по всем контрольным объемам для уравнений (9). Расчеты проводились по этому критерию с точностью до 10-6 на равномерной сетке. В расчетах принималось H0=D; d/D=0,5; ds/D=0,05; b/d=0,2; Ha/H=0,4, где D - диаметр аппарата; H0 - высота невозмущенной поверхности жидкости над дном аппарата; ds - диаметр вала. Результаты расчетов представлены на рис. 1-2 в меридиональной плоскости аппарата в виде линий тока радиально-осевой циркуляции. Мешалка создает потоки жидкости, которые вызывают циркуляцию жидкости по объему аппарата. Окружная циркуляция, называемая также первичной, связана с вращением массы жидкости вокруг оси вращения мешалки. Существенную роль в перемешивании играет вторичная радиально-осевая циркуляция, которая накладывается на основную окружную циркуляцию. Наблюдается образование двух крупномасштабных вихрей, способствующих перемешиванию жидкости и расположенных соответственно сверху и снизу от мешалки. Мешалка вызывает вращательное движение жидкости в аппарате. Когда центробежные силы малы, то это движение приводит к незначительному понижению уровня жидкости у вала мешалки (рис. 1). Рис. 1. Картина линий тока в аппарате при Re=100, Fr=0,05. Увеличение чисел Рейнольдса и Фруда связано с ростом центробежных сил, что находит отражение в усилении радиальнотангенциальной конвекции. В свою очередь это приводит к углублению образовавшейся центральной воронки, характерной для аппаратов с мешалками (рис. 2). Рис. 2. Картина линий тока в аппарате при Re=500, Fr=0,2.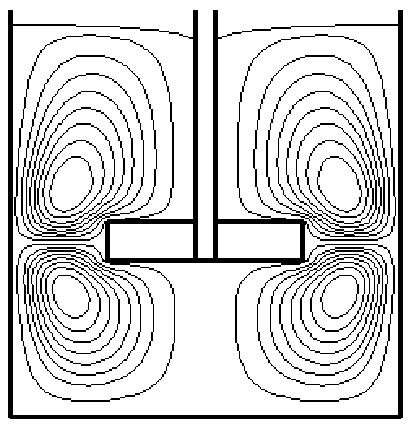
Список литературы Расчет скорости циркуляции жидкости со свободной поверхностью в аппарате с мешалкой
- Стренк, Ф. Перемешивание и аппараты с мешалками. -Л.: Химия, 1975. 384 с.
- Холланд, Ф. Химические реакторы и смесители для жидкофазных процессов/Ф. Холланд, Ф. Чапман. -М.: Химия, 1974. 208 с.
- Манусов, Е.Б. Расчет реакторов объемного типа/Е.Б. Манусов, Е.А. Буянов. -М.: Машиностроение, 1978. 112 с.
- Лойцянский, Л.Г. Механика жидкости и газа. -М.: Наука, 1978. 736 с.
- Патанкар, С. Численные методы решения задач теплообмена и динамики жидкости. -М.: Энергоатомиздат, 1984. 152 с.
- Harlow, F.N. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface/F.M. Harlow, J.E. Welch//Phys. Fluids. 1965. V. 8, No. 12. P. 2182-2189.
- Калиткин, Н.Н. Численные методы. -М.: Наука, 1978. 512 с.


