Расчет скорости плазмохимического травления кварца

Разработка новых дифракционных оптических элементов (ДОЭ) требует создания микрорельефа ДОЭ с размерами зон единицы микрон [1], чего невозможно добиться без использования современных материалов и уникального технологического оборудования. В [2] представлены результаты исследования бинарных фокусаторов мощного лазерного излучения, выполненных на кварцевых подложках, с высотой микрорельефа более микрона и минимальными размерами зон 13 мкм.

При изготовлении ДОЭ на кварцевых подложках наиболее целесообразно использование в технологическом процессе плазмохимического травления (ПХТ), определяющим параметром которого является скорость травления обрабатываемого материала. Ее оценке посвящено значительное число работ [3, 4, 5]. Однако в большинстве из них используются параметры, реальное определение которых представляет значительные трудности, связанные с оценкой характера распределения химически активных частиц (ХАЧ) [6].

В настоящей работе предлагается физикоматематическая модель плазмохимического травления, позволяющая осуществлять расчеты скорости травления, используя реальные параметры режимов ПХТ.

V р - средняя скорость теплового движения ХАЧ, см/с.

Согласно [4] длина свободного пробега и средняя скорость теплового движения ХАЧ описываются выражениями:

А =

p f х6X10-

I

- ₌ Г 8кт_ ²

V p

V п m )

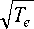
Обоснование выбора модели

Рассмотрим критерии выбора модели плазмо-

химического травления [3]:

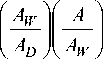
D

k * L d >>  1 и

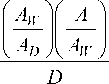
k * L d <<  1,

где A D - площадь сечения диффузии, см²; A W - площадь пластины, см²; A - площадь травления, см²; L d - длина диффузии ХАЧ, см; к * - константа скорости травления, см/с; D - коэффициент диффузии, см²/с.

Выполнение первого неравенства (1) означает, что травление материала протекает по диффузионному механизму, в то время как выполнение второго подтверждает выбор кинетической модели травления.

Для анализа данных неравенств необходимо рассчитать значение коэффициента диффузии по формуле [4]:

D = 3 ^ V p ,

где А - длина свободного пробега ХАЧ, см;

где f - частота высокочастотного (ВЧ) возбуждения электрического разряда, равная 13,56 МГц; T e -электронная температура, К; р - рабочее давление в камере, Па; к - постоянная Больцмана, Дж/К; Т -температура, при которой проводился технологический процесс, К; m - масса ХАЧ, кг

Расчет электронной температуры произведем по формуле:

Te = 1 ■ Ee , (5) k где Ее - энергия электронов, соответствующая параметрам плазмы. Так как травление материала осуществлялось в плазме CF4 при рабочем давлении в камере, равном 1,5*10-1 Па [2], то, согласно [7], энергия электронов равна Ее =1,3*10-18 Дж. Осуществляя расчет величины Te по формуле (5), получим Te =94 000 К.

Учитывая, что в травлении материала принимали участие радикалы фтора, подставим в формулы (3) и (4) известные значения f = 13,56*10 6 Гц, T e =94 000 К, р =1,5*10 '1 Па, к =1,3 8*10 " ²³ Дж/К, Т =423 К, m =3,15*10 ^-26 кг, и получим с ледующие значения величин X , V_p : X =5*10^-2 см, V_p =6,87*10⁴ см/с. Тогда коэффициент диффузии, согласно выражению (2), будет равен D =11,45*10² см²/с.

Подставляя в (1) известные экспериментальные значения A w =A D = A =45,34 см², к* =10^-7 см/с , L d =5*10^-4 см, а также D =11,45*10² см²/с, получим значение меньше 1, что соответствует кинетической модели травления.

Отличительной стороной дифракционных решеток является достаточно большая протяженность дифракционных щелей при сверхмалой их ширине. Поэтому рассмотрим возможность применения кинетической модели для описания процесса ПХТ ДОЭ.

Согласно [3] диффузионное приближение может быть использовано только при выполнении неравенства А <<  d , где А - длина свободного пробега

ХАЧ; d - характеристический размер системы (в нашем случае характеристический размер ДОЭ [8]). При ПХТ в реакторе диодного типа в диапазоне давлений 10-100 Па выполняется равенство X =100-10 мкм, следовательно, для реактора и пластины это условие выполняется, а для элемента топологии, то есть непосредственно в области травления (щели дифракционной решетки), в которых практически всегда выполняется равенство X ® d , этим приближением необходимо пользоваться осторожно. При использовании технологических режимов травления дифракционного микрорельефа выполняется неравенство X >>  d (550 мкм>>1-13 мкм). Это означает полное совпадение условия применения кинетической модели в области травления канавки. В реальных условиях для усиления бомбардировки поверхности подложки на нее подают отрицательное смещение величиной 200-3 00В, которое формирует направленное движение ХАЧ в область травления. В этом случае процесс ПХТ может быть описан свободномолекулярным движением ХАЧ, что не противоречит правильности применения кинетической модели ПХТ.

Оценка скорости ПХТ

В рамках кинетической модели для описания скорости ПХТ наиболее приемлемо аналитическое выражение вида [3]:

0,233 S_nM ( ^kT/ )12

V =----- p _м m^m   Nsum ,         (6)

PNA где V - скорость плазмохимического травления, см/с; M - молекулярный вес травимого материала, г/моль; р - плотность материала подложки, г/см3; Na - число Авогадро, 1/моль; Nsum - концентрация ХАЧ, участвующих в химических реакциях, 1/см3.

Функциональной величиной в этом выражении является концентрация ХАЧ, участвующих в травлении. В настоящей работе в качестве травимого материала используется кварц, а источником химически активных частиц, как уже упоминалось ранее, являются радикалы фтора, концентрацию которых непосредственно в окне травимой канавки вблизи поверхности кварца обозначим через N .

Расчет концентрации ХАЧ, взаимодействующих при ПХТ с поверхностью подложки, произведем с учетом следующих соображений.

При ионной бомбардировке кварца травление осуществляется за счет чисто химического механизма [4]:

SiO 2 + 4F * > SiF ! Т + О 2 Т .                    (7)

Образование реактивных частиц, обеспечивающих травление, происходит непосредственно на поверхности кварцевой подложки в результате ионно-молекулярных взаимодействий ионов CF ^ с молекулами CF 4 [7]:

CF 4 + CF ₃ ⁺ >  2 CF ₃ + F * ,                 (8)

где ионы CF ₃ ⁺ образуются при диссоциации молекул CF ₄ электронным ударом в газоразрядной плазме [4]:

CF 4 + e >  CF ₃ ⁺+ F * + 2 e . (9)

Скорость диссоциации dN/dt , описываемой реакцией (8), в этом случае может быть определена из равенства [7]:

dN⁼N^d  ¹ '" „> I Ч E ) ,      ⁽¹⁰⁾

T              Xj1J"xa4"L у где Ni - поток ионов на поверхность подложки в ион/(см2 с); CTd - поперечное сечение диссоциации молекулы в см2; Е - теплота адсорбции [9], Дж; Мхач - молекулярная масса ХАЧ, г/моль.

В случае плазмохимического травления при заданных условиях (бомбардировка поверхности ионами) для практических расчетов можно принять N i ® 0,3 ■ 10¹⁵ ион / см ² с ; ст d ® 0,3 ■ 10 ^{- 14} см ² [7], тогда произведение N i хст d будет равно приблизительно единице.

Решение дифференциального уравнения (10) относительно N при начальных и граничных условиях

N (0) = 0, N ( t ) = const

будет иметь вид:

N = N -у d [ 1,4 -10^: T

, 22

p j 4M хач Т у

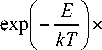
х ( 1 - exp( -X t ) ) ,

P I E 1

где X = 1,4 ■Ю у d           expl--I; t- время kT хач технологического процесса.

Знак минус в первом экспоненциальном множителе выражения (12), указывает на то, что увели- чение температуры стимулирует процесс диссоциации, и, следовательно, увеличивает концентрацию частиц, осуществивших ее. Поскольку эти частицы и осуществляют ПХТ, то их концентрацию N можно принять в качестве концентрации ХАЧ. Однако непосредственно в химическое взаимодействие с кварцем войдут не все продиссоциировавшие частицы, так как некоторая их часть способна отразиться от поверхности подложки. Доля первых определяется коэффициентом прилипания а. Таким образом, количество ХАЧ, осуществивших химическую реакцию с кварцем при первом взаимодействии, мож- но описать равенством:

N = N_t ^ d ^[ 1,4 -10^: I

-22

у хач у

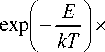
х (1 - exp(-Xt ))■ а где а - коэффициент прилипания, а количество отразившихся ХАЧ N1 будет описываться выражением:

f

N 1 = N i a d 1,4 - 10

I

х ( 1 - exp( -A t ) ) - (1 - a ).

22 Р

. IM_Y tT \ хач у

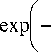
E ) ---|х kT У

При взаимодействии радикалов c поверхностью канавки, например в точке А (рис.1), часть ХАЧ, обладающих достаточной энергией, отражаются и могут снова оказаться в точке А , то есть способны осуществить ПХТ. Это адекватно образованию дополнительной концентрации частиц, способных взаимодействовать с материалом подложки. Данные частицы могут существенным образом изменить процесс ПХТ, поэтому возникает необходимость их учета при расчете скорости травления кварца, например, в плазме CF₄ .

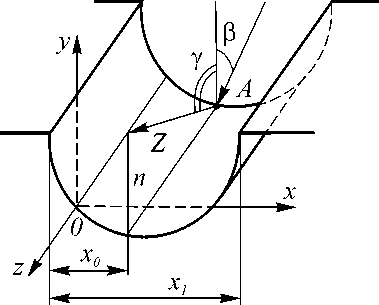
Рис.1. Профиль канавки.

Для малых величин энергий радикалов используемых в ПХТ в большинстве практических случаев удобней использовать косинусоидальный закон отражения ХАЧ. В этом случае при заданных энергиях частиц плотность вероятности повторного попадания в рабочую зону можно описать выражением:

1 cos у cos в

P =   "        2      ^,

П r

где r – расстояние между точками отражения и химического взаимодействия ХАЧ, см; у -угол вылета ХАЧ из точки отражения; в - угол падения ХАЧ в точку рабочей зоны.

Тогда количество таких частиц N^/ можно опи-

сать равенством вида:

f

N / = N 1 P = N i ^ _d 1,4 х 10 2 ²

V

^ жтх V хач у

х exp f- E ^ ( 1 - exP( ^Р/ ) ) - ( 1 - a ) ^f -l ^{cos z} c^os ^e ) .

V kT У                   V n    r2    У

При многократном отражении общее количество частиц, вернувшихся в рабочую зону, и число частиц, провзаимодействовавших с поверхностью

кварца в области травления, согласно работе [6] и с учётом выражений (16), (13) можно описать выражениями вида:

N / = 1 N ^

n ₂ id

1,4 х 10 ²²

V

p

J Мг J

V хач у

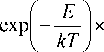
х ( 1 - exp( -A t ) ) - ( 1 - a ) cos у¹ cos в¹ J— R l ^{r //}

где у / , p / - проекции углов вылета у и падения в на плоскость XOY ; dl ^/ - элемент дуги рассматриваемого профиля при фиксированном z (см. рис.1); r // - длина проекции r на плоскость XOY,

N = N ^d ^fM - 10

V

. 22 P

>1 М хач Т J

f E )

exp l--1х

^{V kT У} (18)

х ( 1 - exp( - 2 t ) ) - a J dl / .

R l

Интегралы, находящиеся в правых частях выражений (17) и (18), являются криволинейными, следовательно, для их точного вычисления необходимо задать подынтегральные функции и представить их в параметрическом виде. Анализируя полученную в работе [2] канавку (рис. 1) с геометрическими размерами равными: ширина канавки - 13 мкм, высота выступа – 1,2 мкм, аппроксимируем ее профиль квадратичной функцией вида:

l / = a ( X - X 0 ) ² ,                            (19)

где a – коэффициент, учитывающий расходимость ветвей параболы; X₀ –величина сдвига параболы вдоль оси OX в координатной плоскости XOY .

Изменение длины проекции r вдоль профиля канавки в плоскости XOY зададим функцией:

r _/z = aX ( X 1 - X ),                           (20)

где X₁ –ширина канавки.

В параметрической форме функции (19) и (20) будут выглядеть следующим образом:

X = t /

< l / = a ( t / - 1 0 ) ² , ^r // = ^{at / (} t 1 ^- t / )

где t e [0; t 1 ] (рис. 1).

Подставляя функции r // , l^/ в параметрической форме в интегралы выражений (17), (18) и осуществляя переход от криволинейных интегралов к обычным, получим интегралы вида:

dl ^/

R l ^{r //}

t U1 + 4a ² ( t¹ - 1 ₀) ² dt ₀ at ( t ₁ - t )

t ₁

J dl¹ = J V1 + 4a ² ( t' - 1 ₀) ² dt¹ ,

^Rl       ⁰

где t₀ соответствует X₀ , а t 1 ^ X 1 .

Интегралы, находящиеся в правых частях (22), (23), легко вычисляются методом замены переменных и имеют решения вида:

V =

о,233 S p M ( ^kTm )^ Р N a

1,4 •Ю ²²

p

^М хач ^T

x

t 1 У ¹ + ⁴ a ² ( t' - 1 о ) ² dt' _      ¹ + ⁴ a ² ( ¹ ' — ¹ о ) ² 1 1 ,

1           //,         =2            /               о + о at (11 —1 )                2a(1 -1 о)           (24)

+ 2 lnf ^ 1 + 4 a ² ( 1 — 1 о)² + 2 a ( 1 — 1 о ) j| о¹ ,

Обозначим правые части выражений (24), (25) через W и W :

W = 21п[(У1 + 4 a ² ( 1¹ — 1 _о ) + 2 а ( 1' — 1 _о)]| о

+ 2

У^{1 + 4 a 2 ( 1} * ^{— 1} о ^{) 2} 1 , 2 а ( 1 ^/ — 1 _о)       1^о

+

( E 1

^x N i ^a d ^ex p l ^——M^{1— ex} p ^{( —} x t ^{) )x} V kT ;

x a W'' + 2(1 — a)cos у / cos в/ x W где

W = 21п[(У1 + 4 a ² ( 1¹ — 1 _о) ² + 2 a ( 1¹ — 1 _о)]| о +

2 У^{1 + 4} a ^{2 ( 1 Z — 1} о ^{) 2} 1 ,

2 a ( 1 / — 1 _о )      I^0,

W1 = "2"У1 + 4a2( 1Z — 1 о)2 (1Z — 1 о) ^1 + и подставим их в (17) и (18). Таким образом, общее количество частиц, вернувшихся в рабочую зону

при многократном отражении, и число частиц, взаимодействовавших с поверхностью кварца в области травления, будет равно:

+-- 1п | У 1 + 4 a ² ( 1 — 1 о ) + 2 a ( 1 — 1 о )

4 a V                                     .

1 ₁ о^.

N ^ =1Nad n 2 i d

1,4 x 1о²²

V

P

М хач Т ,

x exp l — E 1 ( 1 — exp( —X 1 ) ) x V kT )

x ( 1 — a ) cos у ^/ cos в ^/ x W

(

N = N a _d 1,4 • 10

V

22 P

J Мхотт

\ хач у

x

x exp l

E |^{( 1 — e}xp^{( —} X ¹ )^ a W 2 kT )

Общее же число ХАЧ, участвующих в химических реакциях, будет описываться суммой:

В выражении (29) значения cos у / , cos ^ / рассчитываются по формулам, изложенным в работе [6], и изменяются в пределах от о до 1. Для нахождения величин N и N 1 необходимо знать значение коэффициента a , который согласно [7] при ионноплазменном нанесении или травлении можно считать равным о,1. Учитывая, что теплота адсорбции при ПХТ изменяется в пределах до 1эВ [9], можно принять для травления кварца в плазме CF 4 теплоту адсорбции равной о,32 эВ. Подставляя в (29) также известные экспериментальные значения: S_p =о,25, М =бо г/моль, к =1,38*1о^-23 Дж/К, Т =423 К, m =3,15*1о^-23г, ^ =2,11 г/см³, N A =6,о2*1о²³ 1/моль, р =1,5*1о^-1 Па, М_хач =19 г/моль, 2 =5,62, а =о,1, 1 1 =13 мкм, 1 0 =6,5 мкм, получим скорость травления кварца, лежащую в диапазоне 3оо< V <7оо А /мин.

N sum = N ⁺ N n .

Подставляя это равенство в выражение для скорости травления (6), получим:

Анализ физико-математической модели ПХТ кварцевой подложки

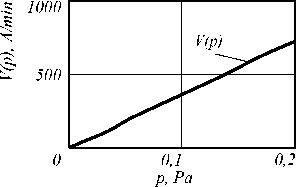
Результаты машинного расчета зависимости скорости травления от технологических параметров ПХТ по формуле (29) представлены на рис. 2.

а)

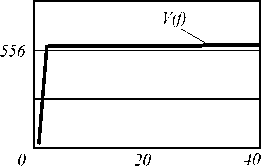
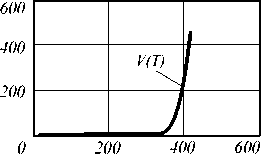
Рис.2. Зависимости скорости травления от времени технологического процесса (а), температуры при которой проводился технологический процесс (б) и давления в рабочей камере (в)

Анализ зависимости, представленной на рис. 2а, показывает, что ее линейность на участке 1 >2 с вытекает из механизма ПХТ. При фиксированной температуре и давлении концентрация ХАЧ яв- ляется величиной постоянной и не должна зависеть от времени технологического процесса, так как частицы, исчезнувшие в результате химических реакций с кварцем, заменяются вновь продиссоцииро- вавшими частицами. Скорость травления в этом случае определяется доставкой ХАЧ к поверхности травления и отводом от нее отработанных частиц, причем, как следует из рис. 2а, данные процессы не-лимитированы, что хорошо согласуется с кинетической моделью ПХТ. Это утверждение позволяет объяснить линейность зависимости V(t) в диапазоне t>2 с, так как, в противном случае, она была бы нелинейна, что соответствовало бы участию в доставке и отводе частиц диффузионных процессов. Увеличение же скорости травления на участке 0

Влияние температуры технологического процесса на скорость травления представлено на рис. 2б. Из работы [4] известно, что от выбора температуры техпроцесса зависит механизм протекания ПХТ. Так, например, при Т<<Т_исп, где Тисп - температура испарения образующихся продуктов реакции, травление возможно только путем распыления. В случае же Т~Т_исп травление осуществляется как за счет химических реакций, так и ионной бомбардировки, однако для увеличения скорости травления необходимо повышать температуру процесса. Наконец, при Т>>Т_исп травление происходит в основном в результате химических реакций. Небольшие изменения температуры процесса сильно влияют на скорость травления материалов [7]. Анализ представленной на рис. 2б зависимости V(T) показывает, что она хорошо согласуется с перечисленными выше условиями. Учитывая, что эксперимент проводился при температуре процесса, равной Т=423 К, которая лежит на экспоненциальном участке кривой V(T) (рис. 2б), то есть когда изменения температуры процесса сильно влияют на скорость травления, можно сделать вывод: травление материала происходило в результате ПХТ, что соответствует эксперименту, изложенному в [2].

Полученная зависимость V(p) (рис. 2в) подтверждает тот факт, что с ростом давления концентрация ХАЧ, участвующих в травлении, увеличивается, и, как следствие этого, увеличивается скорость травления материала, что также хорошо согласуется с экспериментальными результатами работы [2].

Заключение

Предложена физико-математическая модель плазмохимического травления кварца, в рамках которой проведен комплексный анализ зависимостей скорости травления кварца от времени технологического процесса, температуры травления и давления в рабочей камере.

Полученные результаты хорошо согласуются с экспериментальными данными, приведенными в известных работах [2, 7].