Расчет скорости звука в аргоне численными методами

Проведен расчет скорости звука в аргоне по данным о радиальной функции распределения, которая определялась двумя разными способами: методом молекулярной динамики и методом интегральных уравнений. Наблюдается удовлетворительное согласие результатов расчета с экспериментальными данными в широком температурном интервале, охватывающем газообразное, жидкое и твердое состояния.

The numerical calculation of sound velocity in argon

Calculation of speed of a sound in argon on the data on radial function of distribution which was defined by two different ways is carried out: a method of molecular dynamics and a method of the integrated equations. The satisfactory consent of results of calculation with experimental data in the wide temperature interval covering gaseous, liquid and firm statuses is observed.

Одним из направлений классической статистической физики конденсированного состояния является разработка метода аналитического и численного решения интегральных уравнений для парной функции распределения. Зная радиальную функцию распределения, при заданном потенциале межмолекулярного взаимодействия можно рассчитать в принципе все термодинамические свойства вещества в конденсированном состоянии [1-4].

В отсутствие дисперсии при частотах порядка 1 МГц скорость звука можно рассматривать как термодинамическую величину, наиболее чувствительную к изменениям структуры в сравнении с другими величинами, характеризующими состояние системы [5, 6]. Расчет скорости звука в простых молекулярных системах через радиальные функции распределения в области перехода из жидкого в твердое стеклообразное состояние может дать определенную информацию о процессе стеклования на микроскопическом уровне [4,7].

В данной работе предлагается расчет радиальной функции распределения аргона в газообразном, жидком и твердом состояниях с помощью двух методов - метода молекулярной динамики (МД) и метода интегральных уравнений для функций распределения. На основе полученных результатов проводится расчет скорости звука.

Рис. 1. Радиальные функции распределения аргона, полученные методом МД при начальной приведенной плотности числа частиц п*=0.946 и конечной температуре Т= 12 К. г* = r/a. 1 - медленное охлаждение, 2 - быстрое охлажде ние

Метод молекулярной динамики. Для МД расчета радиальной функции распределения в качестве входных данных были заданы концентрация п, температура Т и количество частиц 10000, которые взаимодействуют в соответствии с потенциалом Лен нар да-Джонса

/г т!2 Г

а

U(r) = Ae

где г - межатомное расстояние, f = 120 k и функции распределения подтверждается

<т = 3,405Е - параметры потенциала для аргона [1, 3], к- постоянная Больцмана. По данным об этих величинах? путем интегрирования уравнений движения каждой из частиц рассчитывались изменения положений атомов при охлаждении в кубе периодичности размером 10x10x10 частиц.

Атомы, размещенные вначале в узлах гранецентрированной кубической решетки, движутся к состоянию равновесного распределения частиц при данной постоянной температуре. Траектория каждой частицы рассматривается как совокупность последовательностей шагов, длина которых пропорциональна интервалам времени At. Элементарные акты случайных смещений всех атомов системы составляют одну итерацию. Через каждые 10000 итераций, соответствующих времени движения системы 10"¹¹ с, приведенная температура Д' = кТ/е понижалась на 0,02 (~ 2,4 К). Скорость охлаждения составляла 1,5-10^й К/мин.

После каждых 10000 МД итераций по известной методике [1] подсчитывалась радиальная функция распределения, характеризующая упорядоченность атомов в системе:

экспериментами по нейтронному и рентгеновскому рассеянию [8].

В ходе МД эксперимента наряду с радиальной функцией g(r) рассчитываются плотность системы р = т-п (гл - масса частицы) и давление р по следующей формуле статистической физики жидкостей [1-3]:

4л-л²_г ,dU(r) з „.

р = пкТ --—-|g(r)—-— г -dV. (3)

6 ' dr

По значениям давления р и плотности р на каждом шаге расчетов можно определить их изменения Др и Др, что дает возможность вычислить скорость звука

/ Эр Г Др           ...

у др у Др где у - отношение теплоемкостей Cp/Cv, а др и др - амплитуды давления и плотности в звуковой волне. Здесь и далее значение параметра у берётся из литературных данных по известным р и р [9-11].

Метод интегральных уравнений. В этом методе для расчёта радиальной функции распределения g(ri2) использовалось уравнение Орнштейна-Цернике [1-3]:

g(^) = ^(r)2) + l =

^l+C^J + nfc^)^)^, которое решалось численным методом Ла-бика-Малневского [12]. Здесь п - концентрация частиц, Л(г) - парная корреляционная функция, С(г) - прямая корреляционная функция. Парная корреляция частиц Л(г) складывается из прямой корреляции С(г), возникающей за счет непосредственного взаимодействия пары частиц, и непрямой корреляции, обусловленной одновременным взаимодействием данной пары частиц с остальными частицами системы.

В качестве входных данных были заданы плотность числа атомов п и температура системы частиц, взаимодействующих согласно потенциалу Леннарда-Джонса (1) с вышеуказанными параметрами £ и а для аргона. В ходе численного решения уравнения (5) рассчитывались плотность р и давление р системы. Таким образом, получив решение уравнения Орнштейна-Цернике (5) при двух достаточно близких значениях концентрации п, далее по фор-

136 муле (4) можно рассчитать значение скорости звука.

Для определения скорости звука по формуле (4) вместо дифференцирования давления р по плотности р можно использовать основное свойство парной корреляционной функции h(r), связывающее её с изотермической сжимаемостью системы [2J:

кТ^— 1 = I + 4яп         .   (6)

С учетом и = р / m из (4) и (6) оконча тельно получаем для скорости звука дующее выражение:

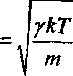
1 + 4лп J/i(r)r26fr сле-

где h(r)=g(r)-I - парная корреляционная функция распределения, определяемая в ходе численного решения уравнения Орн-штейна-Цернике (5), отношение теплоемкостей у находится так же, как и в предыдущем способе.

Обсуждение результатов* На рисунках 2 и 3 приводятся результаты расчета скорости звука в аргоне методом молекулярной динамики при медленном и быстром охлаждении в интервале от 300 до 30 К при давлениях 1 и 40 атм., охватывающие газовую, жидкую и твердую фазы. Для сравне ния на этих же рисунках приведены данные расчета скорости звука методом интегральных уравнений по формуле (7) в газообразной, метастабильно-газовой и жидкой фазах аргона, где уравнение (5) имеет решения. Здесь же даны экспериментальные значения скорости звука в аргоне [9-11 ].

Как видно, наблюдается вполне удовле творительное согласие расчетных данных по скорости звука в газообразном аргоне, полученных методом МД (2) и методом интегральных уравнений (5), как между собой, так и с экспериментальными данными [9-11], что свидетельствует о корректности обоих способов расчета скорости звука.

Скачки величины скорости звука на рис. 2 и 3 соответствуют фазовым переходам системы. В точке Т~ 90 К происходит конденсация пара (рис. 2), в точке Т ~ 86 К -кристаллизация жидкости, а при температуре Г ~ 75 К наблюдается переход системы в аморфное состояние. Переходу систе мы из газообразного состояния в жидкое соответствует скачок при температуре Т ~ 150 К, конденсация жидкости наблюдается при температуре Т ~ 80 К, а её амортизация - при температуре Т~ 60 К (рис. 3).

При этом точки, соответствующие скорости звука, рассчитанной с помощью интегрального уравнения Орнштейна-Цернике (5), имеют продолжение в области переохлажденного пара (рис.2, участок 2), что свидетельствует о справедливости этого уравнения в области метастабильных состояний.

В области жидкого аргона (рис. 3, участок 4) имеется небольшое систематическое расхождение между данными ho скорости звука, полученными методом интегральных уравнений и МД методом при медленном охлаждении. Лучшее согласие с экспериментом дает метод интегральных уравнений, что, на наш взгляд, обусловлено погрешностями итерационной процедуры при расчете радиальной функции распределения g(r) методом МД. Область жидкого состояния при атмосферном давлении (рис.2, участок 4) значительно уже, чем при давлении 40 атм. (рис.3, участок 4), что согласуется с фазовой

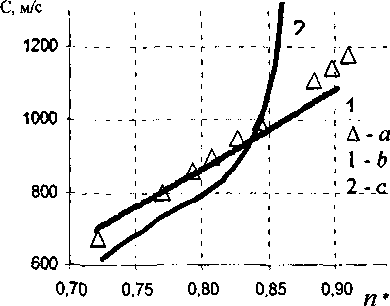
Рис. 4 Зависимость скорости звука с в аргоне от приведённой плотности п при Т=120К. а - эксперимент [4], b - расчёт по (4), с - расчёт по (7)

гласуется с фазовой диаграммой аргона [4]. Скорость звука в жидкости при быстром охлаждении имеет заметно меньшие значения, особенно при давлении 1 атм. (рис.2, участок 4), чем при медленном равновесном охлаждении. По-видимому, это обусловлено тем, что при быстром охлаждении частицы жидкости не успевают перестроиться в структуру равновесной жидкости и имеют больший коэффициент сжимаемости, чем у более плотной равновесной жидкости.

Значения скорости звука на границе газ-жидкость (рис.3, участок 3), рассчитан-

137 ные с помощью уравнения Орнштейна-Цернике (5), показывают, что это уравнение имеет решение в метастабильной области перегретых жидкостей.

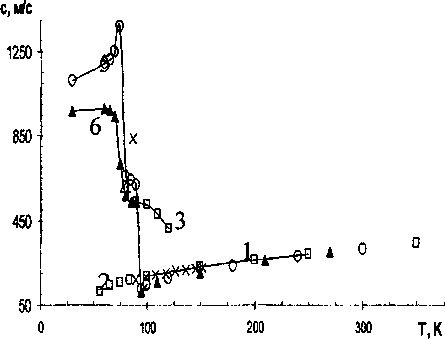
Рис. 2. Зависимость скорости звука в аргоне от температуры при давлении 1 атм. а - МД расчет при медленном охлаждении, b - МД расчет при быстром охлаждении, выражение (4); с - метод интегральных уравнений, выражение (4); d - эксперимент [7]; 1-газ, 2-переохлажденный газ, 3- перегретая жидкость, 4 - жидкость, 5 - кристалл, 6-стекло.

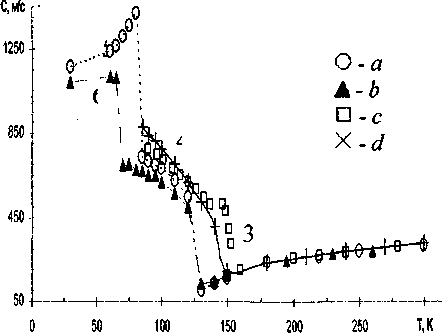
Рис. 3. Зависимость скорости звука в аргоне от температуры при давлении 40 атм. а - МД расчет при медленном охлаждении, b - МД расчет при быстром охлаждении, с - метод интегральных уравнений, выражение (4), d - эксперимент [7]. 1-газ, 3- перегретая жидкость, 4 - жидкость, 5 - кристалл, 6-стекло

На рис. 4 приведены результаты расчета скорости звука по формулам (4) и (7) в газовой фазе аргона методом интегральных уравнений в зависимости от приведенной плотности п - ист3. Там же даются экспериментальные данные [9-11]. Как видно, лучшее совпадение с экспериментом дает формула (4), хотя радиальная функция распределения g(r) получена при численном решении с помощью одного и того же уравнения Орнштейна-Цернике (5). Это обусловлено, на наш взгляд, тем, что при вычислении скорости звука по формуле (4) наибольший вклад дают значения радиальной функции распределения g(r) при малых значениях г, где значения функции g(r) и dUjdr достаточно велики. А на результат расчета по соотношению (7) влияют значения функции h(r)=g(r)-l при больших значениях г. Сравнение данных, полученных с помощью выражений (4) и (7), фактически равносильно сравнению точности определения различных частей радиальной функции распределения g(r). Поэтому отмечен ное расхождение свидетельствует о некоторой термодинамической несогласованности использованного приближённого уравнения Орнштейна-Цернике.

Переход из жидкого в аморфное стеклообразное состояние является ярко выраженным кинетическим явлением, зависящим от скорости охлаждения и скорости структурной перестройки кинетических единиц [13,14]. Поэтому граница перехода определяется условиями проведения эксперимента [4, 15]. При быстром охлаждении молекулы не успевают перестроиться в кристаллическую структуру, в результате чего случайная структура жидкости оказывается «замороженной» и характеризуется очень большими, практически бесконечными, временами релаксации, что фактически означает независимость функций распределения от времени. Это позволяет рассчитывать термодинамические свойства вещества в конденсированном состоянии, включая фазовые переходы.

Таким образом, расчет скорости звука в аргоне методом молекулярной динамики

138 и методом интегральных уравнений для функций распределения приводит к вполне разумным результатам в газообразном, жидком и твердом состояниях, включая области фазовых переходов. Предлагаемый подход применим не только в равновесных состояниях системы, но и в неравновесном стеклообразном состоянии.