Расчет скорости звука в ксеноне методом молекулярной динамики
Автор: Цыдыпов Ш.Б., Герман Е.И., Нестеров А.С., Чекмарев Н.В.
Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu
Рубрика: Физика
Статья в выпуске: 3, 2010 года.
Бесплатный доступ
Рассмотрены возможности расчета радиальной функции распределения простых жидкостей методом молекулярной динамики и расчета на этой основе скорости звуковых волн. Приведены результаты расчетов для ксенона при различных параметрах состояния.
Молекулярная акустика, компьютерное моделирование, фазовые переходы, ксенон
Короткий адрес: https://sciup.org/148179490
IDR: 148179490 | УДК: 534.21
Calculation of sound velocity in xenon with the help of method of molecular dynamics
The possibilities of calculation of radial function distribution of simple fluids and sound velocity by the method of molecular dynamics are presented. Results of calculations for xenon at various parameters of state are given.
Текст научной статьи Расчет скорости звука в ксеноне методом молекулярной динамики
Скорость распространения упругих возмущений в среде определяется особенностями структуры (конфигурациями частиц системы), определяемыми силами межчастичного взаимодействия. Следовательно, скорость звука в среде должна определяться корреляциями частиц среды, описываемыми, в частности, радиальной функцией распределения. Поэтому радиальная функция распределения, получаемая при МД-моделировании, использована нами для расчета скорости звука в неупорядоченных состояниях ксенона при различных параметрах состояния.
Радиальная функция распределения, необходимая для расчета скорости звука в аргоне, определялась нами методом молекулярной динамики. В качестве входных данных были заданы плотность числа атомов n и температура системы частиц, взаимодействующих согласно потенциалу
Леннарда-Джонса
U ( r ) = 4 ε
r
12 о
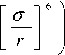
где r – межатомное расстояние, ε = 232·k и σ = 3,98Å – параметры потенциала для ксенона [1], k – постоянная Больцмана.
В ходе численного моделирования фазовых траекторий системы частиц ксенона рассчитывались плотность ρ и давление p системы. Путем последовательных малых изменений концентрации n частиц по формуле
c = γ ∂∂ρp ≈ γ ∆∆ρp можно определить скорость звука при любых возможных значениях плотности ρ и давления p системы, при известном отношении теплоемкостей γ = Cp/Cv.
Вместо численного дифференцирования давления p по плотности ρ для определения скорости звука по (1) можно использовать основное свойство парной корреляционной функции h(r), связывающее ее с изотермической сжимаемостью системы [2, 3]:
kT | ^Tn I = 1 + 4 nn \ h ( r ) r 2 dr (2)
I d p ) T
С учетом n = ρ / m из (1) и (2) получаем выражение для вычисления скорости звука
c
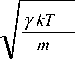
( ) - 1
•1 1 + 4 n n J h ( r ) r 2 dr I
I 0 )
где m – масса частицы, h(r)=g(r)-1 – парная корреляционная функция распределения, определяемая в ходе численного моделирования с помощью радиальной функции распределения g(r) :
g ( r ) =
1 dN 4 π ⋅ r 2 dr n .
На рис. 1 приведены усредненные по всем направлениям радиальные функции распределения атомов ксенона, полученные при постоянных параметрах состояния (T=300К, n*=1.1, P=2200 атм) и при скорости охлаждения 1,5·1014 К / мин с 300 до 100 K. Как видно, при постоянных параметрах состояния (сплошная линия) получается радиальная функция распределения жидкого ксенона, а при быстром охлаждении наблюдается (пунктирная линия) заметное расщепление второго максимума этой функции на два пика, что является признаком аморфизации (стеклования) системы [5].
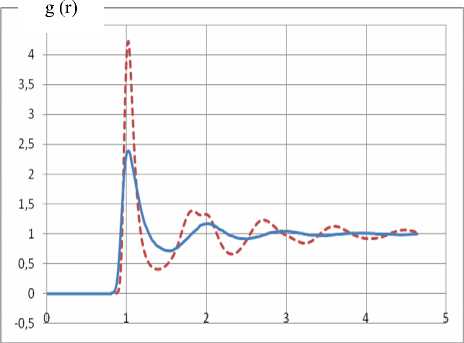
Рис. 1. Радиальные функции распределения ксенона, полученные методом МД при начальной приведенной плотности числа частиц n *=1,1 и конечной температуре T=100 K. r*=r/σ. Сплошная линия - медленное охлаждение, пунктир - быстрое охлаждение
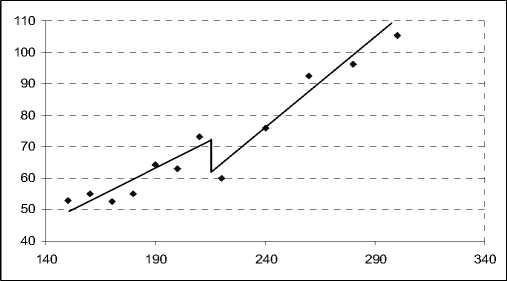
Рис.2. Зависимость скорости звука в ксеноне от температуры при постоянной плотности n*=1.1 и начальной плотности 2200 атм.
Переход из жидкого в аморфное стеклообразное состояние является ярко выраженным кинетическим явлением, зависящим от скорости охлаждения и скорости структурной перестройки кинетических единиц. Поэтому граница перехода определяется условиями проведения эксперимента [6, 7]. При быстром охлаждении молекулы не успевают перестроиться в кристаллическую структуру, в результате чего случайная структура жидкости оказывается «замороженной» и характеризуется очень большими, практически бесконечными временами релаксации, что фактически означает независимость функций распределения от времени. Это позволяет рассчитывать термодинамические свойства вещества в конденсированном состоянии, включая фазовые переходы.
На рис. 2 показаны результаты расчета скорости звука в ксеноне по формуле (3) при постоянной плотности. Скачок скорости звука около 225 К соответствует фазовому переходу флюид-жидкость при охлаждении с постоянной плотностью.
Как и должно быть [8, 9], скорость звука во флюиде ксенона (участок выше 225K) увеличивается с ростом температуры, а в жидком ксеноне (участок ниже 225K) также увеличивается, что связано с ростом давления при повышении температуры и постоянной плотности.
Таким образом, расчет скорости звука в ксеноне методом молекулярной динамики приводит к вполне разумным качественным результатам при различных параметрах состояния, включая области фазовых переходов. Предлагаемый подход применим не только в равновесных состояниях системы, но и в неравновесном стеклообразном состоянии.
