Расчет собственных частот и форм колебаний трубопроводов с помощью программного комплекса
Автор: Прокофьев А.Б.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Надёжность, динамика и диагностика машин
Статья в выпуске: 2 т.1, 1999 года.
Бесплатный доступ
Разработан программный комплекс для расчета собственных форм и частот колебаний трубопроводных систем. Приведена математическая модель, положенн ая в основу разработанного программного комплекса. Выполнено экспериментальное определение собственных частот трубопровода на двух упругих опорах с консольным концом и их сравнение с результатами расчета.
Короткий адрес: https://sciup.org/148197551
IDR: 148197551
Текст научной статьи Расчет собственных частот и форм колебаний трубопроводов с помощью программного комплекса
Институт акустики машин, г. Самара
Разработан программный комплекс для расчета собственных форм и частот колебаний трубопроводных систем. Приведена математическая модель, положенная в основу разработанного программного комплекса. Выполнено экспериментальное определение собственных частот трубопровода на двух упругих опорах с консольным концом и их сравнение с результатами расчета.
Одной из задач в решении проблемы снижения виброакустических нагрузок в гидромеханических системах энергетических установок различного назначения является задача определения собственных форм и частот колебаний трубопроводов. Ее решение позволяет определять возможность возникновения механических резонансных колебаний, места реализации максимальных значений вибропараметров, а также, в частности, является основой для расчета виброакусти-ческой активности трубопроводной системы под действием пульсирующего потока рабочей среды.
Во многих работах [1, 2, 3, 4] даются приближенные методы определения собственных частот и форм колебаний трубопроводов. Основным недостатком подобных методов, приводящим порой к значительным количественным погрешностям расчета, являются упрощения, принимаемые при учете краевых условий (геометрических и динамических условий, налагающих ограничения на свободу перемещения концов трубопровода, а также на изгибающий момент и поперечную силу). Основные варианты способов закрепления трубопроводов, рассматриваемые в этих работах, следующие:
-
1) свободный конец трубопровода;
-
2) жесткая заделка конца трубопровода;
-
3) конец трубопровода закреплен шарниром.
Во всех этих работах при расчете не учитывается жесткость (или податливость) опор крепления трубопровода. Это связано, по-ви-димому, с необходимостью проведения сложных и громоздких вычислений, реализация которых без применения вычислительной техники практически невозможна.
В данной работе предпринимается попытка расчета собственных форм и частот колебаний трубопровода с учетом жесткости его опор при помощи современной вычислительной техники (персональных компьютеров) и программных средств, специально разработанных для этой цели. Методика расчета базируется на методе Крылова. Определение собственных форм и частот колебаний трубопровода осуществляется интегрированием исходного дифференциального уравнения свободных поперечных колебаний прямого стержня [5]. Форма главного колебания (собственная форма), устанавливающая закон распределения максимальных (амплитудных) отклонений точек оси трубопровода от равновесного расположения, описывается общим интегралом:
y(x)=AS(kx)+BT(kx)+CU(kx)+DV(kx), (1) где y(x) - отклонения точек оси трубопровода от равновесного расположения;
A,B,C,D - произвольные постоянные, подобранные так, чтобы для функции y(x) выполнялись краевые условия, т.е. условия закрепления концов трубопровода;
S(kx),T(kx),U(kx),V(kx) - функции Крылова;
|
S ( kx ) = у ( chkx |
+ cos kx ) , |
|
T ( kx ) = у ( shkx |
+ sin kx ) , |
|
U ( kx ) = У ( chkx |
- cos kx ) , |
|
V ( kx ) = У ( shkx |
- sin kx ) , |
Таблица 1. Краевые условия
|
Краевое условие |
Обозначение |
Аналитическое выражение |
|
Конец трубопровода свободен |
у " = 0 у '" = 0 |
|
|
Жесткая заделка конца трубопровода |
^^^^^ |
у = 0 у ' = 0 |
|
Шарнирное закрепление конца трубопровода |
у = 0 у" = 0 |
|
|
Закрепление конца трубопровода в упругой опоре. |
^^^^^^^^^ |
у " = 0 Е1у ” = су |
( тт + m W>2
4 ò æñ k = Л , y (x ) = AS (kx) + BT (kx)+
EI ,
w c - собственная круговая частота; тт - погонная масса трубопровода; m - погонная масса рабочей жидкости, содержащейся в трубопроводе;
E - модуль упругости;
I - момент инерции поперечного сечения трубопровода.
Краевые условия выражаются соотношениями, представленными в таблице 1.
Одним из преимуществ использования функций Крылова и записи формы главного колебания в виде (1) является то, что можно сразу написать выражение общего интеграла, удовлетворяющего условиям на конце x = 0 и содержащего только две постоянные, которые определяются из условий на другом конце x = 1 (здесь 1 - длина трубопровода).
В случае наличия промежуточной опоры выражение (1) для записи формы главного колебания несколько модифицируется. Можно показать [5], что в этом случае собственная форма записывается в виде:
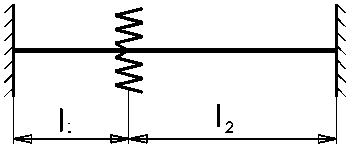
Рис. 1. Трубопровод с жесткой заделкой по концам и упругой промежуточной опорой
+ CU ( kx ) + DV ( kx ) при 0 < x < 1 1 y ( x ) = AS ( kx ) + BT ( kx ) +
+ CU ( kx ) + DV ( kx ) +
+
kRUV ( k ( x - ^
при 1 1 < x < 1 1 + 1 2
Значение величин 1 1 и 1 2 определяется из рассмотрения рис. 1.
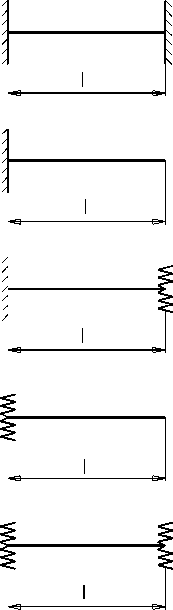
На рис.2 представлена классификация, охватывающая все возможные варианты крепления трубопровода на двух и трех опорах (в классификации не рассматривается случай шарнирного закрепления, так как случай идеального шарнира на практике не встречается, а лишь является упрощением опоры, обладающей высокой поперечной жесткостью и некоторой угловой жесткостью). Предлагаемая классификация положена в основу разработанного программного комплекса по расчету собственных частот и форм колебаний трубопровода. Алгоритм расчетной части программы продемонстрируем на двух примерах:
-
1) трубопровод на двух упруго закрепленных относительно поперечных перемещений концах;
-
2) трубопровод с жестко закрепленными концами и промежуточной упруго закрепленной опорой.
Краевые условия в этом случае:
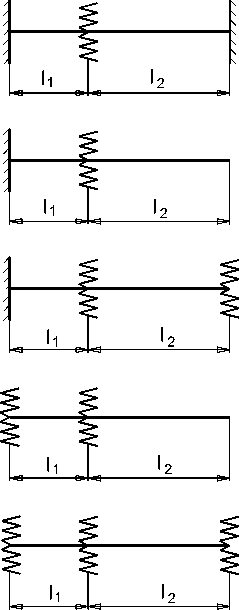
S ( 0 ) = 1, 1 T ( 0 ) = 0, U ( 0 ) = 0, V ( о ) = 0- .
Отсюда C=0 .
Тогда общий интеграл (1), удовлетворяющий для рассматриваемого случая краевому условию у ' *(о ) = 0 , имеет вид:
y(x)=AS(kx)+BT(kx)+DV(kx) (3).
Из второго краевого условия при x=0 , получаем:
k3EI(AT(0)+BU(0)+DS(0))=c1(AS(0)+BT(0)+DV(0)), или с учетом (2)
k3EID = c1A, откуда
A =
k3EI D c1
Рис. 2. Классификация схем
Тогда общий интеграл (1), удовлетворяющий условиям на конце x = 0 , имеет вид:
У ( 0 ) = у" ( l ) = 0, EIy" ( 0 ) = C i y ( 0 ), Ely” ( l ) = c , y ( l )
Подставим краевое условие у'' ( о ) = 0 в выражение (1). При этом необходимо дважды продифференцировать функции Крылова. Выражения последовательных производных по x от функций S(kx),T(kx),U(kx),V(kx) до третьего порядка включительно приведены в таблице 2. Получим:
AU(0)+BV(0)+CS(0)+DT(0) = 0
Значения функций Крылова при x=0 имеют значения:
j( x ) = BT ( kx ) + D
k EIS ( kx ) + V ( kx ) c1
Условия при x=l выражаются уравнениями:
( 33FJ x)
BV ( kl ) + D k---U ( kl ) + T ( kl ) = 0,
V c l 0
B ( k 3 EIU ( kl ) - c 2 T ( kl ) ) +
+ D
kE (k3 EIT ( kl ) - c 2 S ( kl ) ) + c 1
= 0.
+ k 3 EIS ( kl ) - c 2 V ( kl )
Исключив B и D, придем к уравнению частот, которое представим следующим об-
Таблица 2. Производные
|
Первая производная |
Вторая производная |
Третья производная |
|
|
S(kx) |
kV(kx) |
k2U(kx) |
k3T(kx) |
|
T(kx) |
kS(kx) |
k2V(kx) |
k3U(kx) |
|
U(kx) |
kT(kx) |
k2S(kx) |
k3V(kx) |
|
V(kx) |
kU(kx) |
k2T(kx) |
k3S(kx) |
Таблица 3. Уравнения частот и форм главных колебаний
k3 EI
Д ( kl ) = V ( kl ) c 1
+ k 3 EIS ( kl ) - c 2 V ( kl )
- (k3 EIU ( kl ) - cj ( kl ) ) •( k - EI- U ( kl ) + T ( kl ) ) = 0.
I c
Вычисление корней уравнения частот ведется численными методами. Для определения ориентировочных данных о расположении собственных частот системы можно пользоваться известными теоремами Рэлея [6].
а.) Если функция Рэлея растет вследствие прибавления к максимальной потенциальной энергии r квадратов вида
Xk (l i ) = ( q Ki l i + ... + qA У (k=1,2,…,r)
без изменения кинетической энергии, то частоты данной системы ww h и частоты измененной w h связаны неравенствами:
W < o h (h = x,2,...n), W h < W + r (h = 1,2,...n - r)
б.) Если функция Рэлея убывает вследствие прибавления к максимальной кинети-
( k 3 EIT ( kl ) - c 2 S ( kl ) ) +
ческой энергии r квадратов вида
Xk (li ) = (qKili + ... + qnln У (k=1,2,…,r), то частоты wwh исходной системы и частоты wh измененной удовлетворяют неравенствам:
W h < w h (h 1 , 2y' n), w h- r < w h (h = r + 1 ,—n )-
Таким образом, из уравнения частот определяются значения k. (i=1,2,3,...) , которые связаны со значениями собственных частот
выражениями
w i = k2 2
EI
mm + тж òæ
Из первого уравнения системы (4) нетрудно определить, что
1 Г k3EI V ( kl ) I c1
U ( kl ) + T ( kl ) I D .
Подставляя A и B, выраженные через D, в общий интеграл (3), получим следующую форму главного колебания (здесь и в дальнейшем постоянные множители опущены): yx ) = k 3 EI S ( kx ) - V^ kEI^O ) + ТШ ) ' + V ( kx )
Из изложенной выше методики наибо-
лее трудоемкая часть расчетов состоит в определении корней уравнения частот. Практически реализация этой части без применения вычислительной техники не представляется возможной. В таблице 3 приведены уравнения частот и форм главных колебаний для рассмотренных в классификации случаев закрепления трубопровода в двух опорах.
-
2) Краевые условия в этом случае (см. рис.1)
y(0) = y'(0) = y(l i + Ц) = У (Ц + Ц) = 0 Ely* (l i ) = cy (l i )
Подставим краевое условие y(0) = 0 в выражение (1). Получим
AS(0) + BT(0) + CU(0) + DV(0) = 0
Откуда с учетом (2) А=0 . Тогда общий интеграл (1), удовлетворяющий для рассматриваемого случая краевому условию y(0)=0, имеет вид:
y(x ) = BT(kx ) + CU(kx ) + DV(kx )
при 0 < x < li
y(x)=BT(kx)+CU(kx)+DVkx) + R V(k(x-1)) k3EI при 11 < x < 11 +l2
Из второго краевого условия при x=0 , получаем:
y" (0 ) = k2 [ BV(0 ) + CS(0 ) + DT(0 ) ] = 0
или с учетом (2) C=0 . Тогда общий интеграл (1), удовлетворяющий условиям на конце x=0 , имеет вид:
y(x ) = BT(kx ) + DV(kx )
при 0 < x < 1 1
y(x) = BT(kx) + DV(kx) + -3— V(k(x - li)) k EI при 11 < x < 11 +12
С учетом краевых условий при x = 1 1 + l2 получаем следующую систему уравнений:
CU(k(l , + l 2 )) + DV(k(l , + l 2 )) + R^- V(kl2) = 0 k3EI
CT(k(l 1 + 1 2 )) + DU(k(l 1 + 1 2 )) + -R- U(kl 2 ) = 0
k EI
К этим уравнениям, содержащим три неизвестных C, D, R, нужно добавить еще одно уравнение, именно, уравнение, получающееся из краевого условия на промежуточной опоре:
k3EI(CV(kl 1 ) + DS(kl1 )) = c(CU(kl 1 ) + DV(kl 1 )
Из (6) и (7) после небольших преобразований получим уравнение частот системы:
U(k(l , +U )
D = T(k(l , + 1 2 ))
k3EIV(kl1) - cU (kli)
V(k(l i + 1 2 ))
U(k(l i + 12» kiEIS(kl1) - cV (kl1)
V(kl 2 )
U(kU = 0
или
D =
a1
a2
a3
b1 d1
b 2 d 2
b 3 d 3
= 0
где a1 = U(k(l1 +12))
a 2 = T(k(l i + 1 2»
a3 = k3EIV(kl1) - cU (kl1)
b i = V(k(l i + 1 2 ))
b 2 = U(k(l i + 1 2 ))
b3 = k3EIS(kli) - cV (kli)
-
di = V(kl2)
d2 = U(kl2)
d3 = 0
Раскрывая определитель, найдем:
D = di(a2b3 - a3b2) - d2(aib3 - a3bi) = 0
Определив корни уравнения частот k. , по уравнению (5) нетрудно определить значения собственных частот системы. Из уравнений (6) и (7) выразим переменные C и R через D . Получим:
C = cV(kl i ) - k3EIS(kl i ) D k3EIV(kl 1 ) - cU(kl 1 )
R k 3 Eii
V^ki l )
eV ( kl 1 ) - k 3 EIS ( kl 1 ) k 3 EIV ( kl 1 ) - cU ( kl 1 )
D
_ x U ( k ( l i + 1 2)) + V ( k ( l i + 1 2))
Теперь мы можем записать уравнение форм главных колебаний:
Таблица 4. Уравнения частот и форм главных колебаний
|
1 |
D = d , (ab - ab ) - d 2 (ab; - ab , ) a , = U ( k ( l 1 + l 2 )) , a 2 = T ( k ( l, + l 2 )) , a 3 = kEiVkl , ) - cdkl , ) , b , = V ( k ( l , + l 2 )) , b 2 = U ( k ( l , + 1 2 )) , b 3 = k3ElSkl 1 ) - cV ( kl , ) , d , = V ( kl 2 ) , d 2 = U ( kl 2 ) j( x ) = - — U( kx ) + V ( kx ) npu0 < x < l , a 3 ,y ( x ) = - — U ( kx ) + V ( kx ) - — I- —a, + b, | v ( k ( x - 1, )) npul, < x < l, + 12 a; ' ' ' ' d, V <4 ‘) ‘ |
|
|
2 |
D = d i ( a2 b 3 - a3b2 ) - d2 ( aib3 - a3b1 ) a , = S ( k ( l , + l 2 )) , a 2 = V ( k ( l , + l 2 )) , a 3 = k3EIV ( kl i ) - сф , ) , b , = T ( k ( l , + l 2 )) , b2 = S ( k ( l , + 12 )) , b 3 = k ElSkl , ) - cVkl , ) , d i = T ( kl2 ) , d 2 = Ф2 ) j( x ) = -—U ( kx ) + V ( kx ) npu0 < x < l , a 3 _y( x ) = - — u ( kx ) + V ( kx ) — —I - —a 2 + a , | v ( k ( x - l , )) npul , < x < l , + 12 a 3 d2 V a 3 J |
|
|
3 |
D = d i ( a2 b 3 - a3b2 ) + d3 ( aib2 - a2 b i ) a , = S ( k ( l , + 12 )) , a 2 = k3ElV ( kl i ) - ciu ( kli ) , a 3 = k3EIv ( k ( li + 1 2 )) - c 2 u ( k ( l i + 1 2 )) , b i = U ( k ( l , + 12 )) , b 2 = kEiSSk ) - c , V ( kl , ) , b 3 = k3EIs ( k ( li + 1 2 )) - c 2 V ( k ( l , + 1 2 )) , d i = T ( kl 2 ) , d 3 = k3ElSkl 2 ) - c 2 V ( kl 2 ) j( x ) = -—u ( kx ) + V ( kx ) npu0 < x < l , a 2 _y ( x ) = - — U( kx ) + V ( kx ) ——I - —a, + b, | v ( k ( x - 1, )) npul, < x < l, + 12 a2 ' ' ' ' d, V a2 ‘ -j |
|
|
4 |
D = d , ( a 2 b 3 a , = V(k(l, + 1 2 )) , a 2 = U ( b , = k-EIU ( k ( l , + 1 2 )) + T ( k ( l , c 1 b 3 =[ k-EIT ( kl i ) + S ( kl , ) | k3EI - C 2 V c i 0 j( x ) = 3T ( kx ) + a3 c y ( x ) = - b 3- T ( kx ) + k^I s ( kx ) + V ( k a3 c1 |
- a 3 b 2 ) - d 2 ( a , b 3 - a 3 b , ) k ( l , + 1 2 )) , a 3 = kEid ^ kl , ) - c2T ( kl , ) , + l 2 )) , b 2 = k-EIT ( k ( l i + l 2 )) + S ( k ( l , + l 2 )) c 1 —s (kd, ) + V ( kl , ) | , d i = T ( kl2 ) , d 2 = S ( kl 2 ) V c i J S ( kx ) + V ( kx ) npu0 < x < l , 1 x ) -—I b, - a^d | v ( k ( x - 1, )) npu l, < x < l, + 12 d, V a3 ) ' " |
|
5 |
D = d i ( a 2 b 3
b 3 = kE^T ( k ( l i + l 2 )) + i -
d 3 = k3 j( x ) = 2T ( kx ) + a 2
|
- a3 b 2 ) + d3 ( aib2 - a2 b i ) ) - c 2 T ( kl , ) , a 3 = k3ElUvk ( l , + 12 )) - c 2 T ^k l , ) , 6 22 b2 =---- -T ( kl , ) + i - c 2 k EiSkl ) - C 2 V ( kl , ) c i V c i 0 k3EIS ( k ( li + 1 2 )) - c3 V ( k ( l , + 1 2 )) , d , = T ( kl 2 ) , EiSkl 2 ) - c 3 V(kl ) ) , S(kx ) + v(kx ) npu 0 < x < l , x ) -— I b, - ai— | v ( k ( x - 1, )) npul, < x < l, + 12 d , V a2 J |
Коды АЦП
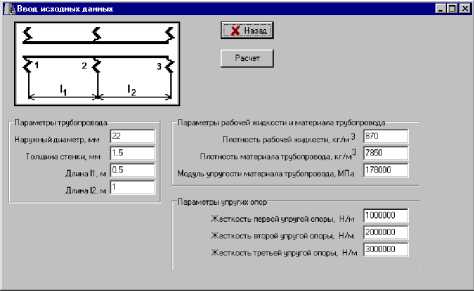
Рис. 3. Примеры экранных страниц программного комплекса
400.00
0.00
-400.00
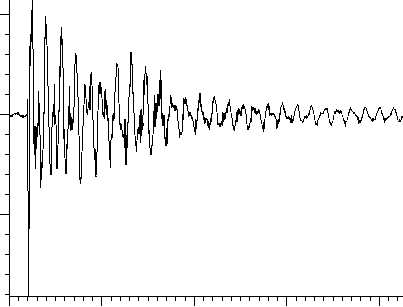
0.88 0.92 0.96 1.00 1.04 t, С
Рис. 5. Осциллограмма собственных колебаний трубопровода
У =
cV(kl , ) - k3EIS(kl , ) k3EIV(kl , ) - cU(kl , )
U(kx) + V(kx)
при 0 < x < l ,
У =
«V™ - kEISk l , ) u(kx) +^ - V(k(x - W k EIV(kl , ) - cU(kl , ) V(kl 2 )
cV(kl , ) - k3EIS(klI) k3EIV(kl , ) - cU(kl , )
U(k(l , + l2>) + V(k(l , + l2>)
при l , < x < l , + l2
В таблице 4 приведены уравнения частот и форм главных колебаний для всех, рассмотренных в классификации, случаев трубопроводов на трех опорах.
Описанные выше алгоритмы реализованы в программном комплексе, ориентированном на персональные компьютеры типа IBM PC и операционную систему Windows 95 или Windows 98. Программный код выполнен на языке C++ с применением интегрированной среды Borland C++Builder.
На рис. 3 представлены окно ввода исходных данных и окно вывода результатов расчета. Имеется возможность вывода результатов расчета в файл данных.
Для проверки достоверности принятых расчетных моделей и работоспособности
1 1 =580 мм
1 2 =208мм
Рис. 4. Схема исследуемого трубопровода программного комплекса наряду с машинным экспериментом был проведен эксперимент на реальном трубопроводе, схема которого представлена на рис. 4.
Экспериментальное исследование собственных частот трубопроводной системы осуществлялось методом простукивания /3/. Основными достоинствами этого известного метода применительно к трубопроводам является высокая производительность, оперативность и несложность применяемой аппаратуры. Он позволяет производить измерения непосредственно на собранной системе, с учетом всех особенностей монтажа, в том числе и с учетом реальных жёсткостей опор трубопровода. На рис. 5. представлена осциллограмма виброускорения, на которой явно видны затухающие колебания. В качестве датчика вибрации применялся преобразователь пьезоэлектрический виброизмери-тельный ДН-4М1 (масса этого датчика 13 г). Сигнал с датчика подавался в измеритель шума и вибраций типа ВШВ-003-М2. Аналоговый сигнал с измерителя шума и вибраций далее поступал в аналого-цифровой преобразователь L-264 фирмы L-card, г. Москва (точность АЦП- 12 бит). Цифровой сигнал с выхода АЦП с помощью программы Gemis Oscilloscope записывался на жесткий диск компьютера. Далее проводился спектральный анализ записанного сигнала.
В таблице 5 приведены экспериментальные и расчетные собственные частоты рассматриваемой трубопроводной системы. Же-
Таблица 5. Экспериментальные и расчётные собственные частоты
Из таблицы видна хорошая сходимость экспериментальных и расчетных значений, по крайней мере, для трех первых собственных частот. Как и следовало ожидать, погрешность определения собственной частоты расчет с увеличением номера этой частоты.
Приведенные данные позволяют судить об адекватности математической модели и возможности использования разработанного программного комплекса для решения задач определения собственных форм и частот колебаний трубопроводных систем.


