Расчет собственных частот транстропных пластин с учетом поперечного сдвига, деформаций поперечного обжатия и поперечного нормального напряжения

Постановка проблемы . Элементами разных строительных конструкций, частью механизмов приборов являются пластины. Поэтому их производство требует более глубокого изучения и повышения точности расчетов, с учетом удовлетворения долговечности и надежности в эксплуатации.

Анализ последних исследований и публикаций. В большинстве случаев авторами неклассических (уточненных) моделей напряженно-деформированного состояния пластин рассматриваются кинетические гипотезы для составляющих вектора перемещения, где тангенциальные составные меняются линейно (С.П. Тимошенко, Е. Рейсснер), относительно поперечной координаты или за законом кубической параболы (С.А. Амбарцумян, В.З. Власов, Х.М. Муштари, В.Г. Пискунов, А.О. Рассказов, О.Ф. Рябов, Р. Кристенсен и др.). Вместе с этим, влияние поперечных деформаций (за исключением В.Г. Пискунова) учитываются частично. Влиянию поперечного обжатия на высшие частоты колебаний пластинки посвящено значительно меньше работ.

Целью исследования есть построение нового варианта модели движения пластин с учетом поперечного сдвига, деформаций поперечного обжатия и поперечного нормального напряжения.

Основные результаты исследования. Для вывода уравнений движения и граничных условий в круглой пластине, используем развития перемещений пластинки U , V , W в направлении координатных осей в виде степенных рядов за поперечной координатой z , которые учитывают обобщенный закон Гука и удовлетворяют начальные условия на поверхностях, а также вариационный принцип Лагранжа для полной энергии системы [2, 5]:

На основании выше изложенного, получим уравнение движения через внутренние силы и моменты, а также граничные условия на границе пластинки:

DA w — 1 — sA +---— q~ — ml 1 — sh A)-------

—ms'

ph2д 4 w "4G" dtr ’

AO — k ²O — ^P ^-^ ; g д1²

д w

Здесь y r =

dw_ 41 dQ d r  5 r dO

1 dw4

---1, r dO5

3v"

2G / G 'V

w = w -

2.4 + X o

3 + Xo

9qh w +--2------

'  40 ( 3 + X o ) E''

h 2 U G i 4       ^h * (1 - “ ) E

8 = 83 v  , 8 = ,

¹    10(1 - v ) ( G'      J ²    20 ( 1 -v ²) E'

8 = 0.1 8+ v" , w = w + 8q^/D, k2 =—■—h”2, l  G,     у q        242!          2 G a =

V G

2 G

, m = 2 p h - маса единицы поверхности пластинки.

Полученные уравнения (2) учитывают дополнительно инерцию вращения поперечных сечений и влияние нормального напряжения a z . Если положить равными нулю параметры 8 и

A ’ , а также А = 1 - а А , то эти факторы в уравнениях (2) учитываться не будут.

Система дифференциальных уравнений свободных поперечных колебаний трансверсально-изотропной пластинки в случае q ₂ = 0 будет иметь вид:

д2 w(r,O, t)      , p d4 w(r,O, t)_

D А2 w (r, O, t) + m (1 - 8 А)-----;—- + m8---= 0,

1  1     dt2            4G

AQ- k ² Q = ^P ^-^ , G d t ²

уравнений (3) для

_A 1 Г д Г d} d f 1 d )" где ^A = - —I r — | ⁺ — I -— I .

r |_d r v d r J dO v r dO J_

Если записать решения системы свободных колебаний пластинки в виде

w ( r , O , t ) = w ( r ) cos n O cos ^ t ,

Q(r, O, t) = f (r) sin nO cos ^t, где ® - круговая частота собственных колебаний пластинки;

n = 0,1, 2, 3,...  - количество волн серединной плоскости в кольцевом направлении, то общее решение можно представить в

Д»-(r) = C J„ (air) + C2 Y, (air) + C31, (Pit) + C4 K, (P,r), где Jn, Y, In, K - функции Бесселя мнимого и действительного аргумента, C - постоянные, которые ищем из граничных условий.

Решения соответствующего характеристического уравнения:

ai =

в =

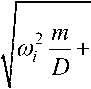
I 2 D J

- й®2

Частоты собственных колебаний пластинки:

® i

=a (1+61“1г5'

В случае сплошной пластинки радиуса R , надо принять

C ₂ = C ₄ = C ₆ = 0 и тогда:

Из граничных условий, когда пластина, шарнирно опертая по контуру r = R: w(R, 6, t) = 0, Mr = 0, Q6 = 0 , получаем трансцендентное уравнение:

(а2 + в )

0,4n2E ( h

« 0i

Jn-MP

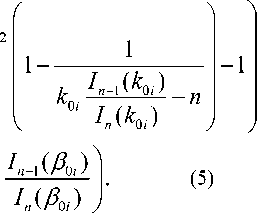
Здесь а0/ = Ra , в/ = Rp , kh = Rkj. Между корнями а а та в существует связь: в =  ।      = ■

На основании изложенных формул и уравнений найдены корни уравнения (5) и соответствующие им частоты, в зависимости от соотношений G/G' и толщины пластинки.

Если в уравнении (5) взять E/G' = 0 , V = 0 и произвести граничный переход когда К₀₁ ^ да , то получим трансцендентное уравнение классической теории тонких пластин:

I n - 1 ^{( а} 0 i ) ^J n ^{( a} 0i ) - I n ^{( a} 0i ) ^J n - 1 ^{( a} 0 i ) =

^{2 a} 0 i

In Kd Jn (a0i)

■

Выводы. Полученные уравнения полностью совпадают по форме с соответствующими уравнениями для пластин классической теории. Отличие только в коэффициентах, которые учитывают поперечный сдвиг и обжатие. Данные уравнения учитывают дополнительно инерцию вращения поперечных сечений и влияние нормального напряжения.

На основании численных результатов установлено, что на частоты собственных колебаний влияют величины поперечного сдвига и обжатия, а также толщина пластинки. Особенно большим это влияние может быть на высшие частоты. При увеличении толщины пластинки от h/ R = 0,05 до h/R = 0,2 все первые три частоты имеют стойкую тенденцию к занижению по сравнению с результатами классической теории тонких пластинок. В случае трансверсально-изотропных пластин явление резонанса может возникнуть гораздо быстрее, чем это предсказывается классической теорией Кирхгоффа-Лява, которая фактически не может определить первую частоту.

• 1.    Амбарцумян С.А. Теория анизотропных пластин. Прочность, устойчивость и колебания / С.А. Амбарцумян. – 2-е изд., перераб. и доп.– М.: Наука, 1987. – 360 с.

• 2.    Васильев В.В. Механика конструкций из композитных материалов / В.В. Васильев. – М.: Машиностроение, 1988. – 272 с.

• 3.    Гершунов Е.М. Расчет круглых и кольцевых пластинок на действие произвольной динамической загрузки / Е.М. Гершунов // Отделение математики, механики. Известия АН СССР. Механика и машиностроение. – 1964. – №6. – С. 89–95.

• 4.    Гринченко В.Т. Равновесие и установившиеся колебания упругих тел конечных размеров / В.Т. Гринченко. К.: Наукова думка, 1978. – 264 с.

• 5.    Лурье А.И. Пространственные задачи теории упругости / А.И. Лурье. – М.: Гостехиздат, 1955. – 491 с.

• 6.    Мелконян А.П. О колебаниях трансверсальноизотропных круглых пластинок / А.П. Мелконян, А.А. Хачатрян // Известия АН Армянской ССР. Механіка. – 1966. – Т. 19. – №3. – С. 26–34.

• 7.    Швабюк В.И. Учет эффекта сжимаемости нормали в контактных задачах для трансверсально-изотропных плит / В.И. Швабюк // Прикладная механика. – 1980. – Т. 16. – №9. – С. 71– 77.