Расчет спектра квантованного по уровням гармонического сигнала
Автор: Тяжев Анатолий Иванович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии радиосвязи, радиовещания и телевидения
Статья в выпуске: 2 т.16, 2018 года.
Бесплатный доступ
В статье приводится вывод формул для расчета спектра сигнала на выходе квантователя с разным числом уровней квантования по оси ординат при поступлении на его вход гармонического сигнала единичной амплитуды. В полученных формулах используются полиномы Чебышева второго рода с нормировкой, которая отличается от нормировки указанных полиномов, используемой в других источниках. В статье также приводятся формулы для расчета спектра сигнала, использующие полиномы Чебышева с данной нормировкой.
Квантованные сигналы, характеристики квантователей, спектры периодических квантованных сигналов, полиномы чебышева второго рода, нормировка полиномов чебышева
Короткий адрес: https://sciup.org/140255690
IDR: 140255690 | УДК: 621.396.98 | DOI: 10.18469/ikt.2018.16.2.09
Текст научной статьи Расчет спектра квантованного по уровням гармонического сигнала
Квантователи сигналов по уровню являются составной частью аналого-цифровых преобразователей (АЦП), от характеристик которых зависят качественные показатели устройств с цифровой обработкой сигналов [6]. Известны выражения, описывающие спектры квантованных гармонических сигналов для ряда частных случаев при ограниченном числе уровней квантования [7]. Цель статьи – получить выражения для расчета спектра квантованного по уровням гармонического сигнала с любым числом уровней и при любых порогах квантования.
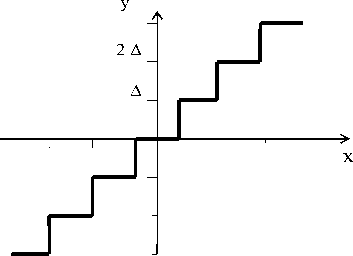
Рисунок 1. Нормированная характеристика квантователя с равномерными шагами квантования по осям х и у
На рисунках 1 и 2 приведены нормированные по обеим осям характеристики y = f ( x ) двух квантователей с равномерным и неравномерным по оси абсцисс шагом квантования, с равномерным по оси ординат шаге квантования Δ = 2/ s и произвольными по оси абсцисс порогами квантования хi , но симметричными относительно оси ординат, то есть хi = – х-i. . Нормировка характеристик квантователей по осям предполагает, что максимальные по модулю значения х и у равны единице.
у
2А -
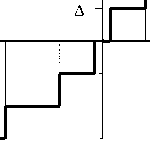
Рисунок 2. Нормированная характеристика квантователя с равномерным шагом квантования по оси у и неравномерными порогами квантования по оси х
Спектр сигнала на выходе бинарного квантователя при подаче на вход косинуса и синуса
Если на вход квантователя подать косинусоидальное колебание с единичной амплитудой x ( t ) = cos 2 πFt = cos φ , где φ = 2πFt , то при бинарном квантовании ( s = 2) сигнал у на выходе такого квантователя будет иметь форму меандра с размахом от –1 до 1. Спектр такого сигнала состоит из гармоник косинуса с частотами kF и амплитудами Аk,2 , определяемыми по формуле, полученной из разложения меандра в ряд Фурье [7]:
Д^ ,= —
\ vcosk(pd J coskydy— jcosA^(/^ = О 71 лП = (4/A'^)sin(^/2). Из этой формулы следует, что в спектре меандра присутствуют только нечетные гармоники входного сигнала, а четные гармоники отсутствуют, так как sin(kπ/2) = 0 при четных значениях k. Если на вход бинарного квантователя подать синусоидальное колебание с единичной амплитудой x(t) = sin(2πFt)= sin φ, то сигнал у на выходе квантователя также будет иметь форму меандра с размахом от –1 до 1, но сдвинутый по фазе на – π/2 относительно меандра при х(t) = cos φ. Спектр такого сигнала состоит из гармоник синуса с частотами kF и амплитудами Аk,2, определяемыми по формуле разложения меандра в ряд Фурье [7]: 1 О । к — [sinA'^x/^H— [sinA'#x/ л 71 о = (4/j^tt)sin2(j^tt/2). Отличие (2) от (1) состоит в том, что в зависимости от k знаки Аk,2 в (1) чередуются от –1 до 1, а в (2) знаки Аk,2 не зависят от k и всегда положительны. Спектр сигнала на выходе квантователя с тремя уровнями квантования при подаче на вход косинуса Рассчитаем спектр сигнала на выходе квантователя с тремя (s = 3) уровнями квантования –1, 0, 1 по оси ординат и двумя порогами квантования х1 и х-1 = –х1 по оси абсцисс при подаче на вход косинусоидального колебания с единичной амплитудой x(t) = cos φ. Отметим, что при уровне входного сигнала х по модулю меньше х1сигнал у на выходе квантователя с тремя (s = 3) уровнями квантования равен нулю. Разложив сигнал у на выходе такого квантователя в ряд Фурье, получим Л/3 = — 1сО8А+/9б/б/9--COSA'^67^ = 4 sin кл / 2 , =-----------cos кф,, кл (3) где Ai = л/2 - фХ , А2 = л/2 + (01, ф\ = arcsinxb Спектр сигнала на выходе квантователя с произвольным числом уровней квантования при подаче на вход косинуса Поступая аналогичным образом, при s = 4 по . 4 . кл/ ~ , х лучим Ак 4 =----sin — (1 + 2 cos кфх). ' Зкл 2 При s = 5 и s = 6 аналогичным образом ^kл sin — 2 (2 cos кфх + 2 cos кф2); Ак 6 =----sin — (1 + 2 cos кфх + 2 cos кф. ' Зкл 2 Здесь φ1= arcsin х1, φ2= arcsin х2, где х1; х2– пороги квантования квантователя по оси абсцисс при х > 0. Из полученных выражений следуют общие формулы для расчета амплитуд гармоник Аk,s квантованного по уровням косинусоидального сигнала при произвольном числе уровней квантования. При нечетном значении s: Ак $ =—” 2^2 cos^Vi, (4) s-1 где Ak,2 определяется согласно (1), m = (s – 1)/2, φi = arcsin хi ; а хi – это i-ый порог квантователя при х > 0. При четном значении s: 4.=^(1+2ЁСО8^)’ (5) 8 1 где Ak,2 определяется согласно (1), m = (s – 2)/2, φi = arcsin хi , а хi – это i-ый порог квантователя при х > 0. Расчет спектра сигнала на выходе квантователя с произвольным числом уровней квантования при подаче на вход косинуса через полиномы Чебышева второго рода Недостатком полученных выражений (4) и (5) является то, что в них вначале по значениям порогов квантователя хi по формуле φi = arcsin хi определяются значения аргументов косинуса, при которых происходят изменения уровня сигнала на выходе квантователя, а затем по этим значениям φi рассчитываются значения cos(kφi), входящие в (4) и (5). Такого сложного вычисления амплитуд гармоник Аk,s можно избежать, если применить полиномы Чебышева, для которых имеет место следующее представление [1]: cos(A'^,) = cos(A' arcsin ф^ = = cos(W2) Тк<х^ + sin(^/2) У^х^. Здесь Tk(xi) – полиномы Чебышева первого рода, Vk(xi) – полиномы Чебышева второго рода с нормировкой Ko(x) = 0, Ki(x) = (1 -х2)1/2; F3(x) = 2х(1 -х2)1/2; Полиномы более высокого порядка вычисляются через полиномы низких порядков по рекуррентной формуле [1]: ^ + 1(х) = 2л-^(х)-К/>_1(х). Подставим (6) в выражения (4) и (5) и получим формулы для расчета амплитуд гармоник Аk,s через полиномы Чебышева второго рода с приведенной в [1] нормировкой. При нечетном s: 8sin2кл/2 кл(з -1) У№), /=1 где m = (s - 1)/2. Аналогичным образом при четном s: , 4(зткл/2)Г1 , . кл^ЦТ7. ^ = < n [l + 2sm—^ИДх,)], (8) кл($ -1) 2 у где m = (s – 2)/2. В формулах (7) и (8) полиномы Чебышева первого рода отсутствуют, так как при подстановке (6) в (4) и (5) сомножителем при Tk(xi) является произведение cos(kπ/2) sin(kπ/2), которое при любых целых значениях k равно нулю. Отметим, что в [2-5] полиномы Чебышева второго рода представлены в следующем виде: £/0(х) = 1, U\(x) = 2x, Ui(x) = 4.x2 - 1 и т.д. Полиномы Vk(x) и Uk(x) вычисляются по формулам [2-5]: Uk1(x) = 2x U^ - Uk_\(x); ^(x)=^_!(x)-(1-X2)1/2. Подставив это выражение в (7) и (8), получим формулы для расчета амплитуд гармоник Аk,s через полиномы Чебышева Uk(xi). Особенности расчета спектра при равномерном и неравномерном шагах квантования по оси абсцисс Практический интерес представляет случай, когда характеристика квантователя имеет равномерный по оси х шаг квантования (см. рис. 1). В этом случае пороги квантования хi определяются по формулам: Xj = (2/ - l)/s при нечетном s; xf = 1i/s при четном s, где i =1; 2; 3 … – номер порога квантования. Для этого случая справедливы следующие предельные соотношения: А1,∞= lim A1,s = 1 при s → ∞; Аk,∞= lim Ak,s = 0 при s → ∞, k > 1. Из этих соотношений следует очевидный вывод, что квантователь с равномерными по осям х и у шагами квантования и с бесконечно большим числом уровней квантования (s → ∞) не изменяет спектр входного сигнала. В цифровых системах связи применяют квантователи с логарифмической зависимостью y = f(x), описываемой выражениями [8]: у =ln(l + //x) прИ g < x< ] . (9) ln(l + /I) у = —при -1 < x< 0, (10) ln(l + Ц) где μ – параметр, определяющий степень сжатия динамического диапазона входного сигнала. Получим выражение для расчета порогов квантования хi квантователя, характеристика которого описывается выражениями (9) и (10). При равномерном по оси у шаге квантования имеем Из (11) получим выражение для расчета порогов квантования х : i Xj = — expf ln(l + //) -1). (12) // V~1 ) Подставив эти значения в выражения (7) или (8), рассчитаем спектр квантованного гармонического сигнала на выходе квантователя с логарифмической характеристикой v ^ M. Аналогичным образом можно получить выражения для расчета порогов квантования хi при других зависимостях y=j^ [9-10]. Заключение Полученные формулы позволяют рассчитать спектр квантованного гармонического сигнала на выходе квантователя с любым числом порогов квантования по оси абсцисс и с любой характеристикой у =ЛД симметричной относительно оси ординат. Полученные формулы дают инструмент для исследования шумовых характеристик квантователей, а также для оптимизации этих характеристик по точностным и шумовым показателям.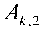
Список литературы Расчет спектра квантованного по уровням гармонического сигнала
- Янке Е., Эмде Ф., Леш Ф. Специальные функции. М.: Наука, 1968. - 344 с.
- Бахвалов Н.С. Численные методы. М.: Наука, 1975. - 256 с.
- Васильев Ф.П. Методы решения экстремальных задач. М.: Наука, 1981. - 288 с.
- Воеводин В.В. Численные методы алгебры. Теория и алгоритмы. М.: Наука, 1966. - 324 с.
- Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977. - 412 с.
- Иванова В.Г., Тяжев А.И. Цифровая обработка сигналов и сигнальные процессоры. Самара: Изд-во ПГУТИ-ОФОРТ, 2008. - 264 с.
- Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Радио и связь, 1986. - 184 с.
- Аппаратура уплотнения ИКМ-12М для сельской связи. Под ред. М.У. Поляка. М.: Связь, 1976. - 160 с.
- Тяжев А.И. Выходные устройства приемников с цифровой обработкой сигналов. Самара: Самарский университет, 1992. - 276 с.
- Тяжев А.И. Операция перестановки и ее применение для исследования радиотехнических устройств и систем // Физика волновых процессов и радиотехнические системы. Т.17, №2, 2014. - С. 59-63.


