Расчет статического деформирования осесимметричных оболочек вращения по дифференциальной модели

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2024PNRPU MECHANICS BULLETIN

Развитие строительных, авиационных, космических, судостроительных отраслей неразрывно связано с использованием тонкостенных конструкций. Наука об оболочках относительно молода: она появилась в XIX в. и стала бурно развиваться в XX–XXI столетиях по пути построения практических методов расчета. Традиционно учёными строились аналитические и приближенные решения для частных случаев геометрических форм, вариантов граничных условий, видов нагрузки, различных моделей материалов. Обзор подходов, методов решения и моделей теории пластин и оболочек приведен в работе [1]. Существенный вклад в исследование деформирования пластин и оболочек был сделан учеными благодаря развитию метода конечных элементов (МКЭ), который является универсальным и постоянно совершенствующимся инструментом в сочетании с современными возможностями вычислительной техники. В большой части инженерной и научной среды сложилось убеждение, что современные CAE-пакеты прикладных программ на основе МКЭ, такие как ANSYS, Femap, Abaqus, MSC.Marc и много других, удовлетворили все потребности как инструменты в исследовании напряженно-деформированного состояния сплошных сред. С этим сложно не согласиться, универсальность и относительная простота программной реализации МКЭ сделала его, пожалуй, самым популярным численным подходом к решению задач механики, в том числе для расчета деформированного состояния оболочек. Тем не менее отдельными учёными предпринимаются шаги по созданию и развитию альтернативных МКЭ-подходов, нацеленных как на решение отдельных задач, так и на создание универсальных подходов.

Интересным и перспективным направлением в развитии альтернативных подходов к расчету оболочечных конструкций представляется применение бессеточных методов перидинамики [2; 3]. В работе [4] применяется метод граничных элементов для расчета оболочечных конструкций, результаты сравниваются с расчетом методом конечных разностей (МКР). В монографии [5] изложен вариационно-разностный подход к расчету конструкций, приведен глубокий обзор работ по уточненным теориям оболочек. В статье [6] изложен метод неявных конечных разностей (МНКР), который позволяет, исходя из формулировки краевой задачи в перемещениях и напряжениях как независимых между собой основных величинах разрешающей системы уравнений, определять напряжения с более высокой точностью, чем МКЭ в форме метода перемещений. В работе [8] для решения задачи устойчивости цилиндрической оболочки под действием неравномерной нагрузки используется метод на основе сплайн-интерполяции. В статье [7] обсуждается и анализируется применение вариационно- разностного метода к расчету линейных и нелинейных задач деформирования тонких и толстых оболочек из композитных и изотропных материалов. В работах [9– 12] используется метод дифференциальных квадратур для аппроксимации производных некоторых дифференциальных уравнений механики и краевых условий, что позволяет свести их решение краевой задачи к решению системы линейных алгебраических уравнений относительно узловых значений разрешающих функций. В [13] приведен численный анализ устойчивости явной разностной схемы высокого порядка для расчета симметричных оболочек вращения под действием импульсных нагрузок. В работах [14; 15] рассматривается деформирование мягкой оболочки из высокоэластичного материала, для расчета применяется метод дифференцирования по параметру, позволяющий свести решение нелинейной краевой задачи к совокупности квазилинейной краевой и нелинейной начальной задач и применить метод начальных параметров решения линейных краевых задач. В работе [16] используется по сути метод пристрелки для решения двухточечной краевой задачи для мембраны как осесимметричной оболочки вращения, проводится анализ устойчивости и построение форм равновесия до и после точек бифуркаций. В статье [17] применяется МКР для расчета оболочки в форме эллиптического параболоида с шарнирно-неподвижным опиранием. В работе [18] МКР применяется для расчета напряженно-деформированного состояния композитной оболочки вращения. В статье [19] рассматривается численное решение МКР уравнений классической теории оболочек для описания напряженно-деформированного состояния сильфона U-образного компенсатора при нагрузке внутренним давлением. В [20] МКР используется для расчета прямоугольной плиты на упругом основании, произведена верификация с результатами расчетов, выполненных с помощью двойных тригонометрических рядов. В статье [21] с помощью МКР проводится анализ устойчивости пластин и оболочек в условиях ползучести для элементов конструкций из материалов, обладающих свойством старения, находящихся под действием длительных нагрузок. В работах [22–25] рассматриваются подходы к расчету взаимодействия оболочечных конструкций с жидкостью.

Настоящее исследование является логическим продолжением и развитием статьи [26] с обобщением уравнений на геометрическую нелинейность, произвольную параметризацию меридиана, учет изменения толщины и поперечного сдвига при деформировании. Для получения численного решения применен алгоритм [27; 28] на основе метода конечных разностей, обладающий лучшей сходимостью, по сравнению с методом пристрелки, используемым в работе [26], а также имеющий возможность получать непосредственную оценку достигнутой точности численного решения.

1. Общие уравнения оболочек в глобальных координатах

Для стройности повествования приведем полные выкладки «от общего к частному» для получения разрешающей системы дифференциальных уравнений.

В трёхмерном пространстве рассмотрим криволинейную поверхность оболочки, которая разделяется координатными линиями (рис. 1, а ), на поверхности возьмем бесконечно малый элемент, образуемый линиями s ₁ , 5 2 , 5 1 + ds_i, s2 + ds 2 , в точке O этого элемента поставим локальную систему координат с тремя единичными векторами e_i, e₂, e₃ (рис. 1, b ).

Уравнение поверхности задаётся радиус-вектором:

r ( s 1 , s 2 ) = x_i ( s_p s 2 ) i_i + x 2 ( s _i, s 2 ) i 2 +

+ x 3 ( s i , s 2

—                                     —

) i 3 = x k ( s i , ^s 2 ) i k ,

где ik – базисные векторы глобальной системы координат; s1 , s2 – криволинейные координаты рассматривае- мой поверхности, по повторяющимся индексам ведется суммирование от 1 до 3.

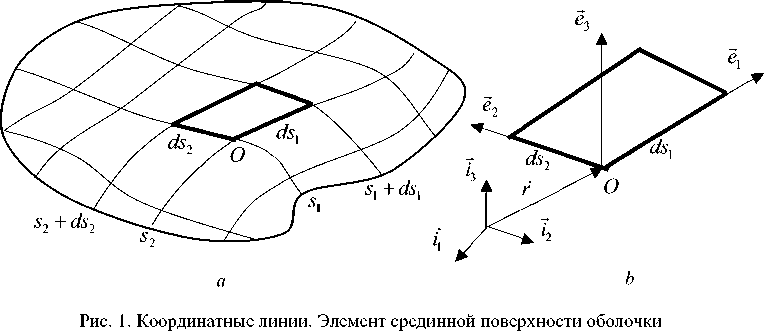
Fig. 1. Coordinate lines. Element of the midsurface of the shell

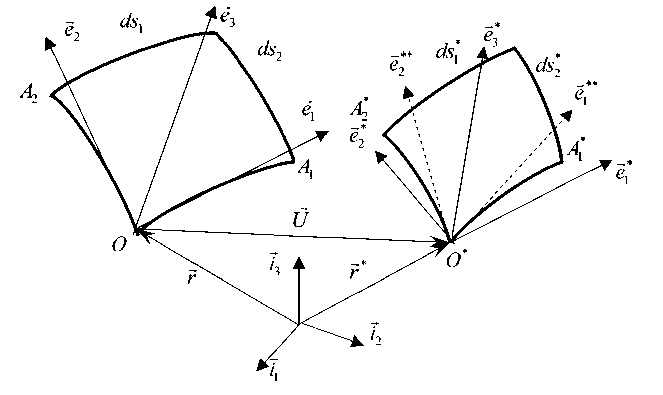
Рис. 2. Перемещение и деформирование малого элемента оболочки

Fig. 2. Displacement and deformation of a small shell element

Векторы локальной системы координат выражаются следующим образом:

— d — — d r — — — el — — , e2 — —   , e — ei X e2 .            (2)

a 5 1          a s ₂

С практической стороны удобно задавать начальную ориентацию с помощью матрицы поворота (матрицы начальной геометрии):

—* e ₁

^— e ₂

— e2

P 21

P 31

P 22

Р з2

P 23

Р зз

— i1

— i2

— i3

^ ei ^— P kik .

Деформация малого элемента (рис. 2) состоит из:

– перемещения параллельно самому себе как жесткого целого и поворота относительно точки O ^* ,

– изменения длин его сторон,

– изменения угла между сторонами.

Поворот малого элемента определим следующим образом:

ds * - ds,        ds * - ds,

61 — —1----1, 62 — —2----2 - относительные удлине- ds1                ds2

ния сторон малого элемента вдоль направлений s ₁ и s ₂ соответственно.

При деформировании векторы локального базиса ^— 1 , e ₂ переходят в e * , e ₂ * . С учетом (3) и (4) повернутые орты будут иметь следующие выражения: ^{—         —}

—, —P^—P k X _k k i k .               (6)

— *      — *

При наличии сдвига ортогональность e ₁ и e ₂ нарушается, и они переходят в ^— 1** , e ₂ ** . Обозначим угол сдвига %, тогда:

— **    — *           — *          — **    — *          — *

e 1 — e 1 cos х + e 2 sin x , e 2 — e 1 sin x + e 2 cos x ,

или

—**      —*           (cos X ek — akjej , где a — I •

( sin x

sin X cos X

^X 11

^X 21

^X 31

^X 12

^X 22

^X 32

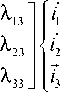
^ ~ i;—x kA ,

Из (2) и (3) можно получить:

——                                       —— dr — e1 ds1 — P1 kikds1, dr — e2ds2 — P2kikds2,      (8)

.     , 1 - cos to                    sin to 1 - cos to

Xii — 1--— (toj+tok),X ij—     ®k +2— to x j * to            to2

. sin to 1 - cos to,

Xi —-- tok. +--5— to to. , i — 1,2,3; j — 2,3,1; k — 3,1,2;

ik                      ki toto

тогда с учетом (6) и (7)

dr" ^{— —} * ds * ^— ( 1 ⁺ 6 1 ) « 1 j p jk ^X kk i k ^ds 1 , dr* ^{— —} 2** ds * ^— ( 1 ⁺ 6 2 ) « 2 j P jk ^X kk i k ^ds 2 , ^{j —} 1,2.

где to _k - проекции вектора конечного поворота (вектора Эйлера) на оси глобальной системы координат.

В результате перемещения параллельно самому себе как жесткого целого точка O займет новое положение O*, длины отрезков ds1 — OAj , ds2 — OA2| изменятся и ста- нут равными O A1 — ds1 , O A2 — ds2. Обозначим

—

Поскольку U — r * - r , то

—

I UU ^— [ ( 1 +61 ) « 1 j p jk ^x kk ^- P 1 k ] ^— k , —

| U — [ ( 1 + 6 2 ) « 2 j P jk X kk -P 2 k ] ^— k .         (10)

d s 2

Уравнения (10) описывают кинематику деформирования срединной поверхности оболочки. Они связывают поворот элемента оболочки, растяжение его сторон и изменение угла между ними с перемещениями элемента.

Несмотря на то, что в основе рассматриваемой математической модели лежит гипотеза Кирхгофа - Лява, подразумевающая малую толщину оболочки и сохранение ортогональности нормалей к срединной поверхности при деформировании, кинематические соотношения (10) можно легко модифицировать для приближенного учёта сдвиговых деформаций, которые вносят ощутимый вклад в изменение кривизны при деформировании толстых оболочек и пластин. Для этого будем рассматривать конечное состояние как суперпозицию деформированных состояний: 1) от изгиба, растяжения, сдвига в плоскости (по гипотезе Кирхгофа - Лява), и 2) сдвига поперек срединной поверхности, что соответствует теории Тимошенко. Таким образом, перемещение за счет сдвиговой деформации вдоль нормали к деформированной поверхности можно записать следующим образом:

— d—5=5 ds;=-ql -з* ds;=-з* ds;= кGh       кGh

—-           —*

T ,^ k X knin

к Gh * , k X k, к Gh *

*

М3 p ^pn nn 1

*

M3 p ^pnn   1

T -                  - *        - *

,    XуРзkРзpXpnindsi = 51 J.dS , где G - модуль сдвига, h* - толщина деформированной оболочки, к - корректирующий коэффициент сдвига прямоугольного сечения, T = T/',-, T2 = T2,1, - векторы внутренних погонных сил на площадках, ортогональных координатным линиям. Аналогично в другом направлении перемещение за счет сдвига будет иметь следующее выражение:

V -     *      7 2,                   - *         - *

dr₂ = ⁵ 2 d 2 =      . ^X kj Р з k Р з p ^X pAd 2 = ⁵ 2 n i n ds 2 . ⁽¹²⁾

кGh коэффициент сдвига п2 /12 < к < 1. Сравнение теоретических значений корректирующих коэффициентов сдвига с экспериментальными приведены в работе [з5].

В итоге кинематические соотношения (10) с учетом поперечного сдвига (11) и (12) запишутся так:

—*

U = [ ( 1 + 6 - ( «„P jk X kn + 5 1 n ) -р , n ] ^- n ,

^ = [ ( 1 + 6 2 ) ( a 2 j P jk X kn + 5 2 n ) -P 2 n ] ^- n .     (1 з)

Вычислим кривизны оболочки в направлении нормали к ней в двух сечениях для недеформированного и деформированного состояний:

k =--- e, , k =---- e , k =--- e₂ , k, =---- e₂ . (14)

1                1" 1            * 1,2                2*2 "x * 2 V / дSj          дSj            дs 2          дs 2

Рассмотрим равновесие элемента оболочки под действием внешней распределенной нагрузки и моментов. По граням элемента прикладываются внутренние погонные усилия и моменты, полученные в результате осреднений напряжений по толщине оболочки (рис. з). Направление погонной силы относительно нормали к грани, в которой она действует, может быть в общем случае произвольным (возможны нормальные, поперечные и касательные усилия).

Дифференциалы параметров поверхности представим в виде ds 1 = A 1 d а 1 , ds ₂ = A ₂ d а ₂ . В этом представлении можно считать а 1 , а ₂ безразмерными параметрами на поверхности.

Для деформированной оболочки имеем ds * = A * d а 1 , ds 2 = A * d а ₂. Уравнение равновесия сил, записанные для деформированного состояния, имеют вид:

1 d( A2* T)     1 д( A* T2) -. . \---- + . . \----- + q = 0

A 1 A ₂ да 1      A 1 A ₂ да ₂

Корректирующий коэффициент сдвига [29-з1] учитывает неравномерность распределения касательных напряжений по толщине оболочки. В середине прошлого столетия для этого коэффициента Миндлин [з2] предложил значение к = п ² /12 , что мало отличается от значения, полученного Рейсснером: к = 5/6 [зз]. Каупер вы-

1 ^д ( ^A 2* ^M 1 )      1    ^д ( ^A 1* ^M 2 )

A * A ₂ *    да ,       A 1* A ₂ *    да ₂

+

1 д г

A 1* да .

—•

1 д-*   -

+ -1 -д— X T2 + Т- = 0,

A ₂ да ₂

числил коэффициент коррекции как к =

—---- [з4].

Жилиным было получено значение к = —-— [зз], и сде-6-V лано предположение, что реальный корректирующий

где T = T_yi / , T ₂ = T _{2 j}i _y - векторы внутренних погонных —* —* —* —*

сил; M 1 = M 1 , i . , M ₂ = M_2ji_y - векторы внутренних моментов; q = q , ! , - вектор внешней распределенной нагрузки; m = -,./,. - вектор внешнего распределенного

момента.

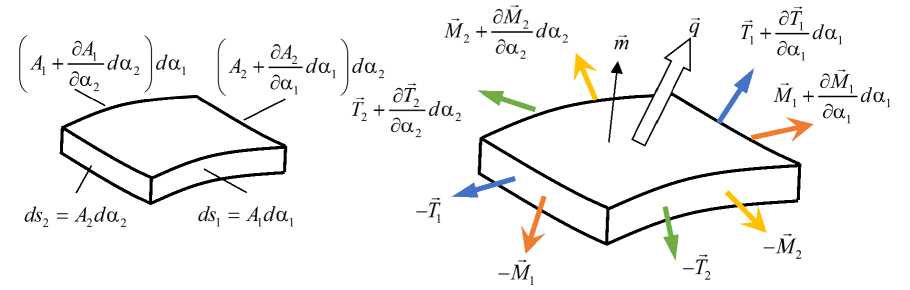
Рис. 3. Равновесие элемента оболочки

Fig. 3. Equilibrium of the shell element

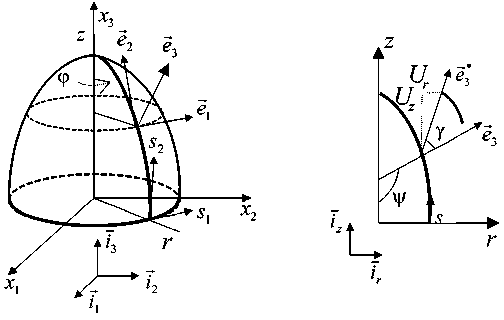
Рис. 4. Геометрия и деформация оболочки вращения

Fig. 4. Geometry and deformation of the shell of rotation

Для замыкания системы уравнений необходимо добавить связь между параметрами деформации и напряжениями и граничные условия. Запишем физические соотношения, полученные В.В. Новожиловым [36] для изотропного материала:

растяжение: е,=—( N -V N ) , е₂=—— ( N -v N ) , (17) 1 _Eh 122 _Eh 21

сдвиг:

X =

2 (1 + v)

Eh

5 =

2 (1 + v)

Eh

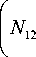
H

R 2

2 (1 + v)

Eh

^N 21

H

^^^^^^e

R 1

12                     12

изгиб: ^K 1 = Eh^ ( M 1 ^-V M 2 ) , ^K 2 = Eh^ ( M 2 ^-v M 1 ) , ⁽¹⁹⁾

Юнга, v - коэффициент Пуассона, e 1 , e ₂ - параметры продольной деформации, % - параметр деформации сдвига, К 1 , к ₂ - параметры изменения кривизны срединной поверхности, т - параметр деформации кручения.

Необходимо отметить, что закон зависимости деформаций от напряжений (17)–(20) может быть заменен на любой другой при необходимости, это не приведет к принципиальному изменению предлагаемого подхода к расчету деформирования оболочек. Кроме того, в уравнения могут быть добавлены силы инерции и рассмотрена задача динамического деформирования, но это выходит за рамки данной статьи и будет опубликовано отдельно.

2. Вывод определяющих уравнений для осесимметричной оболочки

кручение:

12HiVl „ T                                    ,

Eh ³

где N 1 = T 1 e * , N ₂ = T ₂ e ₂ * - продольные силы, 5 = T 1 e 2* = T 2 e * - сдвиговое усилие, M 1 = M 1 e * ,

При осесимметричном деформировании оболочки вращения (рис. 4) координатная сетка на оболочке остается ортогональной, то есть параметр сдвига X = 0 . Введем в рассмотрение цилиндрическую систему координат с ортами

M 2 = M 2 * — изгибающие моменты, H = M 1 e * = M ₂ — * -крутящий момент, h – толщина оболочки, E – модуль

i r = cos ф i 1 + sin ф i ₂, i ^ =

- sin ф i 1 + cos ф i ₂, i z = i ₃. (21)

Радиус-вектор срединной поверхности будет иметь следующий вид:

*                     *

r ( s, ф) = r ( s ) —_r + z ( s ) —_z ,                (22)

где r ( s ), z ( s ) – параметрические уравнения меридиана оболочки.

В качестве параметров поверхности возьмем s ₁ = r ф , s ₂ = s . Выпишем векторы локального базиса:

— = - sin ф —1 + cos ф —2 = —ф, e2 = Г s cos ф - + r s sin ф —2 + z, si3 = r sl+ z, sL (23) e3 = z,s cosф —1 + z,s sinф —2 - rs —3 = z,sir - rs —z, где символ в нижнем индексе после запятой означает дифференцирование по этой переменной.

Таким образом, матрица (3) для осесимметричной оболочки будет иметь вид:

P =

- sin ф r_s cos ф

z _s cos ф

cos ф 0 r sin ф z, , s , s z , sin ф - r

, s , s

Выпишем кривизны недеформированной срединной поверхности:

,   д e^- ki = T" e = дs

₁                              ¹                           _z (25)

—(-zs sinф —1 + zs cosф —2)(-sinф — + cosф —2) = ——, d e -    /          -       . - k2 = V"e2 = (zss cosф —1 + z.« sin ф— 2 - rss —3 )X ds 2

X ( r_s cos ф — 1 + r_s sin ф — ₂ + z , _s — ₃ ) = z , _ss r_s - r_ssz , _s .

Вектор поворота (5) в случае осесимметричного деформирования (см. рис. 4) имеет следующий вид:

o = -Y- =-yPik— = Ysinф —1 -уcosф —2,(27)

Таким образом: o ₁ = Y sin ф , o ₂ = -Y cos ф , to " = 0, |to| = Y. Элементы матрицы поворота для преобразования (4) примут вид:

Х_п = 1 - (1 - cos y ) cos² ф , X ₂₂ = 1 - (1 - cos y ) sin² ф , X ₃₃ = cos y , X ₁₂ =- (1 - cos Y )sin ф cos ф , X ₂₃ = sin y sin ф , X ₃₁ =- sin y cos ф , ⁽²⁸⁾ X ₁₃ = sin y cos ф , X ₂₁ = - (1 - cos Y )sin ф cos ф , X ₃₂ =- sin y sin ф .

Векторы погонных внутренних усилий и моментов в силу осевой симметрии деформирования имеют вид:

T = Т 1 ф г,, T 2 = т 2 т 2z — z , M ^- 1 = M 1 s e = M 1 st,s — + M 1 s z , s — z , M 2 = M 2 ф — ф .

Кривизны координатных линий на деформированной поверхности с учетом (6), (24) и (28) запишутся следующим образом:

, d ^- ( - .         1      d ^- ( - .

ki = —г e =^---г — e ds1       r (1 + e1) дф

= ———7 (z s cos Y+ r sin Y r(1 + 61 )v ’’

.. дe3* -,        1     дe( -, k2 = Г e2 =3------7

д s ₂        ( 1 + 6 ₂ ) д s

= (T+6-j⁽ *"-^r ■ - ^r- z ■ ⁺' > •

Вычислим изменение кривизн при деформировании:

.                1

A k 1 = k 1 - k 1 =—---- -( z s cosY⁺ r s ^sinY )— -, ⁽³²⁾

r (1 + 6) ’’

^{A k} 2 = ^k ’ ^{- k} 2 = ( 1 + ¹ 6 2' ) ( z ■ ss r s - r ss z ■ s ⁺ Y , s ) - ( ^z , ss r: s - r ss z , s ) .⁽³³⁾

Необходимо отметить что в выражения для изменения кривизн (32) и (33) входят начальные кривизны. Начальная кривизна меридиана k ₂ = z_ssr_s - r_ssz_s содержит вторые производные функций r ( s ) и z ( s ) , что может усложнить формирование исходных данных при наличии скачков кривизн. Обычно в таких случаях производят стыковку отдельных решений на каждом участке, где кривизна непрерывна и нет изломов. Программная реализация метода конечных разностей, применяемая в данной работе для решения краевой задачи, позволяет проводить стыковку решений в автоматическом режиме без участия расчетчика.

При малых продольных деформациях (удлинениях) выражения для приращения кривизн примут следующий вид

A k ₁ = - [ z , _s ( cos y- 1 ) + r s _s sin Y ] , A k ₂ =y , _s ,    (34)

то есть если деформации предполагаются малыми по смыслу задачи, то задание начальной кривизны не обязательно.

Вектор перемещений в случае осесимметричного деформирования выглядят следующим образом:

U = U_r ^- r + U z — z = U r cos ф - + U r sin ф — 2 + U_z ^- ₃. (35)

Преобразуем выражения для производных перемещений:

д U 1 д U 1_rr -    -

=       = U r —ф = 61 —ф , дs1 r дф r отсюда следует выражение для окружной деформации (удлинения):

6 1 = ¹ U r •                      (36)

r

Из соотношения (13) с учетом (28) и (12) получим:

*                *

U" = UT = E C ^{1 + 6} 2 )( d r ⁺ d z ⁶ ) - r s ^{] —} r ⁺ d s 2 ds

+ [(1 + 62 )( dz - d,.6)-Z s ] *., где dT, - dT,

6= z 2'J 2z , dr =(rs cosY-z,$ sinY), к Gh               ’          ’ dz = (rs sin y+ z s cos y) ■

Таким образом получены выражения для изменения кривизн (32) и (33) выражение для удлинения в окружном направлении (36) дифференциальные уравнения для перемещений (37). Получим уравнения равновесия и физические соотношения с учетом изменения объема при больших перемещениях.

До сих пор (выше) использовалась естественная параметризация функций – s ₁ s ₂ s за исключением уравнений равновесия (15) и (16) где введены безразмерные параметры на поверхности - a 1 , a ₂ и параметры Ламе A ₁, A ₂. На практике удобно пользоваться произвольной безразмерной параметризацией. Для случая осесимметричной оболочки введем безразмерный параметр длины меридиана 5 , то есть s = s ( 5 ) ■ Определим параметры Ламе следующими соотношениями:

ds dsx = Axda, = rdф, ds2 = A2da2 =—d5,    (39)

d 5

то есть параметры Ламе    A1 = r, A 2 = s 5,   и da1 = dф, d a2 = d5 ■

Вычислим производные, входящие в уравнения равновесия (15), (16) по безразмерным параметрам поверхности:

d [A2 (1 + 62) 71 ] = d [ A2(1 + 62)Т1ф — ] = da1

dT.i—

= A2(1 + 62)-^ = - A2(1 + 62T —r, d ф d [ A (1 + 61) 72 ] = d [ r (1 + 61) 72 ] = da 2

_ d ^[ r ( 1 ^{+ 6} 1 ) ^T 2 r ] * d ^[ r ( 1 ^{+ 6} 1 ) ^T 2 z ] *

d 5        —r + d 5

d [ A2 (1+ 62) M 1 ] da, d (M ^r i— + M^zi)

= A2 (1 + 62)                        = A2 (1 + 62) M 1 srs—ф, d ф d [ A (1+ 61) AM 2 ] = d [ r (1-г) M 2ф —ф ] = d [ r (1+ 61) M 2ф ] *

da2               d 5                d 5

Таким образом, уравнения равновесия сил в проекциях на оси цилиндрической системы координат i_r , i_z имеют следующий вид:

d [ r ( 1 + 6 . ) T 2 r ]

-------"ZZ--A2 (1 + 62)Т1ф + rA2 (1 + 61 )(1 + 62 ) qr = 0, d5                                              (40)

d [ r ( 1 + 6 1 ) T 2 ]

——d^——+rA 2 (1+61 )(1+62) qz = 0, где — = qrir + qziz - внешняя нагрузка. Уравнение равновесия в проекции на ось —ф удовлетворяется тождественно.

Уравнение равновесия моментов в проекции на ось — _ф :

d [ r (1 + 6, ) M ₂ ]

^{[ (} d ₅      * ^] + A ( 1 + 6 2 ) M 1 , r , +

+ rA ₂ ( 1 + 6 1 )( 1 + 6 ₂ ) x                     (41)

X[ T _{2 r} ( r_s sin Y+ z_s cos y ) - T _{2 z} ( r_s cos Y- z_s sin y ) ] = 0.

Физические соотношения (17)–(20) для осесимметричной оболочки примут следующий вид:

*

N 1 = T ₁ ф = -г ( 6 1 +V6 2 ) ,          (42)

1 -V

N 2 = T _{2 r} ( r_s cos Y- z _s sin y ) +

+ ^T 2 z ( r s ^sin Y+ ^z , s ^cos y ) = Eh -y ( ⁶ 2 ^+v6 1 ) ,

1 -V

Eh ^*3

^M 1 = ^M 1 s =           ( ^A k 1 ^{+VA k} 2 ) ,

12 ( 1 -V ² )

Eh ^*3

^M 2 = ^{- M} 2 ф = —т:--- 2y ( ^{A k} 2 ^{+VA k} 1 ) , 12 ( 1 -V )

где h ^* – толщина деформированной оболочки (при коэффициенте Пуассона V >  0 при растяжении происходит утонение, а при сжатии - утолщение); 6 1 , 6 ₂ - меры продольных деформаций.

В настоящее время тензор логарифмической деформации является одной из наиболее популярных мер деформации тела при решении геометрически нелинейных задач [37], логарифмические деформации выражаются через удлинение следующим образом:

6 1 = ln ( 1 + 6 1 ) , 6₂ = ln ( 1+ 6₂ ) . (46)

Необходимо отметить, что при малых деформациях или при геометрически линейной постановке задачи удлинения и меры деформации равны: 6 1 = 6 1 , 6 ₂ = 6 ₂. Это следует в том числе из формул (46).

Определим изменение толщины при деформировании через изменение объема. До деформации элементарный объем

V = р • h • ds* • ds *, после деформирования объём можно выразить так:

V * = p • h * • ds** • ds * = p • h • fh •(I + e* )-(1 + e* )• ds* • ds *, где новую толщину представим в виде произведения старой толщины и некоторой функции, описывающей изменение толщины, подлежащей определению: h = h • fh. Имеет место следующее отношение:

V* _P-h• fh •(* + e*)•(* + e*)• ds* • ds*V                 p • h • ds* • ds*= fh •(* + e*)•(* + e*), с другой стороны, известно [38–40]:

*

— = (*+e* )(* + e2 )(* + 63), следовательно, fh = 1 + e3.

Запишем обобщённый закон Гука:

e* = E[o* -v(g2 +03)J, e* = E[°* -v(o +O3)J,E3 =  [o3-v(°* +o*)J ,

E так как рассматриваются тонкие оболочки, положим 03 v(e* +e*)

=0, тогда e3 =---------, и с учетом (46) в итоге имеем следующее выражение для функции изменения толщины:

M * _s = thf h ( A k * + vA k * ) ,             (5*)

M * ₉=- t f ³ ( A k * +vA k * ) ,          (5*)

из (50) определим меру деформации в меридиональном направлении:

^s , 5 f h

f h = ^exP

v v-*

В практических целях важно привести уравнения к безразмерному виду. Введем в рассмотрение безразмерные величины следующим образом:

s = s , h = h , r = r , z = z , U = U , T = ⁽* 2 ) T , I I I I I Eh t

M ,

Eh ²t*

где t - характерный геометрический размер оболочки (например: длина меридиана, радиус). Кроме того, перейдем к параметризации функций с помощью 5 .

Физические соотношения (42)–(45) с учётом (48) перепишутся следующим образом:

T*Ф = fh (e* +ve*),

[T*r (r5 cos Y-z 5 sin y) + T*z (r5 sin Y+z 5 cos y)1 = s^ [      "          A !                    ,s /j (50)

= fh (e* +ve*),

x [ T * r ( r ^ cos у- z 5 sin y ) + T * z ( r ^ sin y+ z 5 cos y ) J -ve * .

Здесь необходимо отметить, что в выражение (53) входит (47), что образует нелинейное уравнение относительно меры деформации e * . В программной реализации это уравнение решается методом простых итераций.

Упростим и перепишем уравнения равновесия (40) с учетом (48) и (39):

dT 2 r d 5

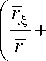
e*-5   If +

( * + e * ) J * r

+

s i(*+£*) r ( * +e , ) "

-         (*-v* )

- s , 5 ⁽ * ^+e* )^r" q-Eh

dT*^ = -fr^+T^^bfIT, - s* (*+e2)h*^^*h d5      ( r (* + e*)J *z ’5V     *^ Eh

d5      t r (* + e*)J *Ф

r _E {* + E₂) - 4(— *4 m 1 ^r (* ^+e * )

T (*+ e*) h

T * _r ( r^ sin у+ z 5 cos y ) -

- T * _z ( r h; cos Y- z , 5 sin y )

q_z ,

Из физического соотношения (5*) выразим y _s , при больших продольных деформациях и выражений для изменения кривизн (32), (33) получим:

Y , s =- ( * ^{+ e} * ) M44 ^-V ( * ^{+ e} * ) ^A k * ^+e * ( z ss r s ^{t h}f h

где A k * =

z , s [^cosY-(¹ + E 1) ] + ^r s sⁱⁿ Y

(*+ e*) r

r ss ^z ,s ) , ⁽⁵⁴⁾

при малых продольных деформациях из выражений для кривизн (34), получим

Y,s =

M * _Ф

t hf h³

где A k * = —[ z_s ( cos Y- * ) + r_s sin y J .

Таким образом, определив y _s по формуле (54) или (55), изменение кривизны A k * будет определено по формуле (33) или (34) соответственно, тогда M _{1 s} может быть определен из физического соотношения (51).

В итоге с учетом (48) и переходом к параметризации по 5 окончательно имеем разрешающую систему 6 геометрически нелинейных дифференциальных уравнений первого порядка относительно 6 функций – U r , U z , Y, T 2 _r , T 2z , M 2 _Ф , описывающих напряженно-деформированное состояние осесимметричной оболочки при больших продольных деформациях, перемещениях и поворотах, что будет иметь следующий вид:

– кинематические соотношения:

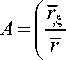
^e 1-⁵ __I _e  -1 ^ГХу

( 1 + 6 1 ) J ’ ^{6 1, 5} = I r^{2 Ur}

⁶ 1 = ^{1 U} r , r

T 2 r d_r + T 2 z d_z

²       s , 5 ^f h ( ⁶ 2 )

_

1) dU T “ ( 1 ^{+ e} 2 ) ( d r ⁺ d z ⁰ ) ^_ ^ ’

²⁾ "" d ^ “ ( 1 ^{+ 6} 2 ) ( d z ^_ d r ⁰ ) ^_ z , 5 ;

– уравнение упругости при больших продольных деформациях:

3) d Y = _ ^{( 1 +}_⁶ 2 ) s _A m ) d 5        hf h      2 ^Ф

^{_ v ( 1 +e} 2 ) s л^А k i ⁺ Sr ( ^z , 55 Г 5 ^_ Г 55 ^z ^ ) - s , 5

где

А k ₂ =

А k1 =     ,1     . ( z,5 [cos Y_(i + 61 )] + Г5 sin y), s ,5r (1 + 61)

? 5s 5 ^{_ 6} 2 ⁽ z 55 ^r,   ^Г 55 z .J .

^{( 1 + 6} 2 ) s ,3

;

– уравнение упругости при малых продольных деформациях:

³⁾ d ? ^{= _} A" ^M 2 ф ^{_ v} s , 5 ^{А k} 1 , ^{d 5}     hf h

1                                                    ?.E где Аk1 = ^4z5(cos?_ 1) + г5 sinY1, Аk2 =— ; (58)

^s , 5 r                                    ^{J              s} , 5

– уравнения равновесия:

di -   S? -             ( 1 _v ² )

• 4)    _/; = _ AT 2 г + 4 bt^ s 5 ( 1 +6 2        ' q r ,

d 5          r                 Eh dT -            (1 _v2)

• 5)    T = _ AT 2 z _ S , 5 (1 + 6 2 )^-^ q z ,     (59)

d 5                    E h

• 6)    ' M / = _ AM _{2 ф} _ ^r4 BM 1 s _ ¹²(1 +6 2) ( T 2 Д _ T 2 z - r ) , (60) d 5                 r h '              '

  – дополнительные выражения и обозначения:

d_r = ( Г , 5 cos ?_ z , 5 sin ? ) , d_z = ( Г⁷^ sin ?+ z , 5 cos y ) ,

₀= E ( d z ^T 2 r _ d r ^T 2z )

К G ( 1 ^_v 2 ) s , 5 ^fh ’

¹ dUT- 1 B rd 5 J

6 2 = exp ( 6 2 ) _ 1,

(1 + 62 )(1 + 61) ’

^v6 1 , ^fh ( ⁶ 2 ) = exP -^( ⁶ 1 ⁺⁶ 2 ) , v_ 1

6 1 = In ( 1 + 6 1 ) ,                      (61)

T 1 _Ф = f h ( 6 1 +v6 2 ) , M 1 s = hf h ³ ( А k 1 + vA k 2 ) .

Необходимо отметить, что имеется два варианта учета изменения кривизн: при больших продольных деформациях (57) и при малых (58). При тестировании уравнений вычисление изменений кривизны по формуле (58) дали лучшее приближение к решениям, получаемым в ANSYS.

Линеаризуем систему уравнений (56)–(60) относительно деформаций, поворотов, перемещений, усилий и моментов, получим геометрически линейную систему уравнений осесимметричной оболочки:

dU                dU

1)       = ^r 5⁶ 2 ^{_ z} , 5 ^{Y+ z} , 5 ⁰ , ²⁾       = ^z , 5 ⁶ 2 ^{+ Г} 5 ? ^_ Г 5 ⁰ ,

3) d ?=_ Д. M d 5     hf h

hf h ³

2 Ф

^r 5 ^_ v^Y , r

4) dT ²- = ( v- 1 ) ^Г^ T 2 r +v z , ⁵ T 2 z + d 5           r r

⁺ (1 ^_v 2 ) ^^e.

5) ^dT 2 ^z =_ ^r , ⁵ t ’ d 5       r ^{2 z}

dM 2 _Ф d 5

_

( 1 _v ²

5             q r

Eh

s

^{, 5} Eh

q z ^,

r

= ^{( v_} 1 ) "Y ^M 2 ф ^_ r

( 1 _v ² ) 4 ^h ?_ ¹² ( ^T 2 r z , 5 _ T 2 zrY , ^x ' r s^ h

где         6 1 = 4 U_r ,

r

E ( z , 5 T 2 r ^_ i ;5 T 2 z )

0 =-------;--------;------ •

К G (1 _v2) s, 5

62 =    (T 2 гГ 5 + T 2 zz 5) _ v61, s ,5          ’

Необходимо отметить, что полученная система линейных дифференциальных уравнений (62) отличается от системы, полученной в работе [26], наличием слагаемых от поперечного сдвига (угол 0), а также множителей И ^ , которые появились при введении произвольной параметризации функций. В работе [26] рассматривается

частный случай системы (62), когда s ^ = 1, что соответствует введению параметризации £ = s / £ .

• 3.    Программная реализация и тестовые расчеты

Полученные уравнения (56)–(62) совместно с краевыми условиями, наложенными на функции в начале и конце меридиана, представляют собой краевую задачу. Для решения краевой задачи был использован алгоритм [27; 28]. Полученные системы нелинейных и линейных уравнений внедрены в код программного комплекса DARSYS [41]. Для аппроксимации производных используются центральные разности и применяется алгоритм отложенной коррекции [27], повышающий точность решения.

Для тестирования уравнений были рассмотрены несколько простейших задач осесимметричного деформирования оболочек вращения. В качестве эталона для сравнения принимались результаты расчета в пакете ANSYS. Для этого разработаны макросы на языке APDL, позволяющие проводить параметрические расчеты при варьировании типа конечного элемента, нагрузки и степени дискретизации модели. В табл. 1–4 приведен набор макросов для расчета составной оболочки. В табл. 1 приведен текст главного макроса, из которого вариативно вызывается конфигурационный файл с конкретной геометрией оболочки, краевыми условиями, типом расчета.

Таблица 1

Макрос ядра для решения тестовых задач на языке APDL

Table 1

Core macro for solving test problems in the APDL

FINISH /CLEAR,START /UNITS,SI /nerr,0,,,,0 /uis,msgpop,3 START = 5 FINAL = 100 *do,E_TYPE,1,3 LEVEL=1 GEOMETRY='UGL1' *Do,VARIN,START,FINAL,1 PARSAV, ALL, Temp, txt /CLEAR,NOSTART PARRES, CHANGE, Temp, txt /PREP7 *ABBR,RELOAD,/INPUT,core,for *USE,GEOMETRY *if,E_TYPE,EQ,1,then ET,1,SHELL181 SECTYPE,,SHELL SECDATA,h fileadd='_181' *elseif,E_TYPE,EQ,2,then ET,1,SHELL43 R,1,h,h,h,h fileadd='_43' *elseif,E_TYPE,EQ,3,then ET,1,SHELL93 R,1,h,h,h,h fileadd='_93' *endif MP,EX,1,2E7 MP,PRXY,1,0.3 MP,DENS,1,7850 AMESH,ALL *if,CLAMPED,eq,1,then NSEL,S,LOC,Y,0 D,ALL,ALL,0 *else

NSEL,S,LOC,Y,0 D,ALL,UY,0 D,ALL,ROTX,0 D,ALL,ROTZ,0 *endif NSEL,S,LOC,X,0 D,ALL,UX,0 D,ALL,ROTY,0 D,ALL,ROTZ,0 NSEL,S,LOC,Z,0 D,ALL,UZ,0 D,ALL,ROTX,0 D,ALL,ROTY,0 ALLSEL,ALL SFA,ALL,,PRES,PRESSURE /SOLU ANTYPE,STATIC NLGEOM,NONLIN SOLVE * if,NONLIN,ne,0,then * GET, isConverged, ACTIVE, 0, SOLU, CNVG *else isConverged=1 *endif *if,isConverged,eq,1,then /POST1 PLDISP,1 n_num=NODE(X0,Y0,0) *GET,Summ,NODE,n_num,U,SUM *cfopen,%filename%%fileadd%,prn,,APPEND * vwrite,VAROUT,Summ %I %G *cfclos *else LEVEL=LEVEL+1 *endif *enddo *USE,'PrintForm.for' *enddo

Таблица 2

Макрос построения геометрии составной оболочки UGL0

Table 2

Macro for initializing the geometry of a combined shell UGL0

Alpha = ACOS(-1)/6 s=sin(Alpha) c=cos(Alpha) L = 0.3 H_ = 0.8 R = 0.5 K,1,0,0,0 K,2,0,0.01,0 K,3,0.5,0,0

K,4,R,H_,0 K,5,(R-L*s),(H_+L*c) L,3,4 L,4,5 AROTAT,1,2,,,,,1,2,90,NN ESIZE,(H_+L)/(NN-1) X0=(R-L*s) Y0=(H_+L*c)

Таблица 3

Макрос управления при варьировании дискретизации составной оболочки UGL1

Table 3

Macro for varying the number of divisions of a combined shell UGL1

filename='UGL1' NN=VARIN h=0.02 *USE,'UGL0'

PRESSURE=1*1e5 VAROUT=VARIN NONLIN=1 CLAMPED=1

Таблица 4

Макрос управления при варьировании нагрузки составной оболочки UGL2

Table 4

Macro for varying the loading of a combined shell UGL2

filename='UGL2' NN=50 h=0.02 *USE,'UGL0' !NROPT,FULL,,ON *if,VARIN,eq,START,then PRESSURE=1e4 P0=PRESSURE *else

*if,isConverged,ne,0,then P0=PRESSURE *endif PRESSURE=P0+5e3/LEVEL *endif VAROUT=PRESSURE NONLIN=1 CLAMPED=1

• 4.    Цилиндрическая оболочка

Рассмотрим задачу о деформировании цилиндрической оболочки под действием внутреннего распределённого давления P (рис. 5). Радиус R = 0,5 м, толщина h = 0,02 м, высота H = 0,7 м, модуль упругости материала E = 2 -10⁷ Па, коэффициент Пуассона v = 0,3. Меридиан зададим следующим образом:

r ( ^ ) = R , z ( ^М- H , ( 0 <^< 1 ) ,       (63)

краевые условия:

при ^ = 0: T 2r = T_z = M _2ф = 0;

при ^ = 1: а) T 2 _г = U z = M 2 _ф = 0 , б) U r = U_z = у = 0 . (64)

На рис. 6 приведены зависимости полного перемещения верхней точки меридиана от числа разбиений, а также деформированные конфигурации, рассчитанные с помощью скрипта APDL (табл. 1–3) в ANSYS и по формулам (56)–(61) в DARSYS при значении давления P = 1,1 -105 Па при свободном опирании (см. рис. 6) и при защемлении (рис. 7).

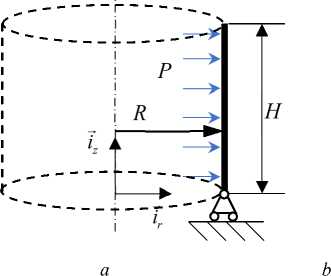
Рис. 5. Цилиндрическая оболочка. Расчетная схема: а – свободная; b – защемленная

Fig. 5. Cylindrical shell. Calculation scheme: a – free; b – pinched

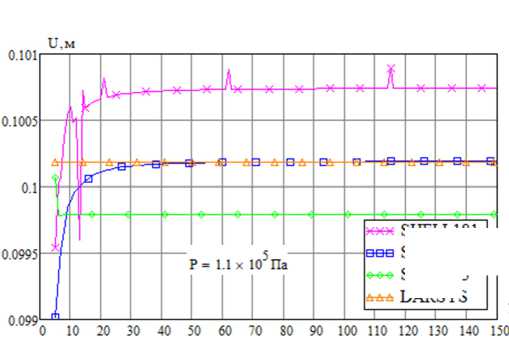
Рис. 6. Сходимость перемещения при варьировании числа разбиений и деформированная конфигурация свободной цилиндрической оболочки

SHELL 181

SHELL43

SHELL93

DARSYS

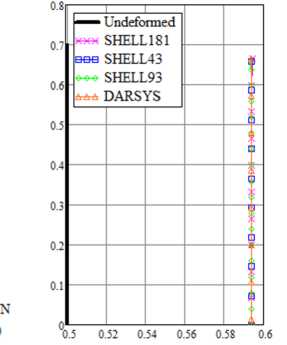
Fig. 6. Convergence of displacement with varying number of divisions and deformed configuration of a free cylindrical shell

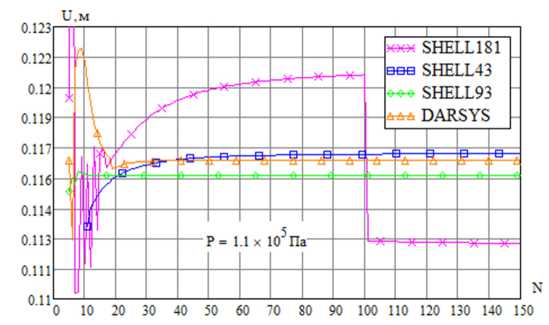
Рис. 7. Сходимость перемещения при варьировании числа разбиений и деформированная конфигурация защемленной цилиндрической оболочки

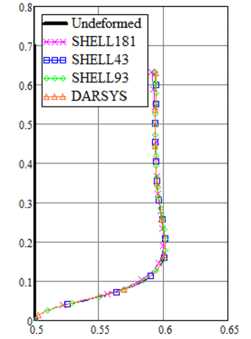
Fig. 7. Convergence of displacement with varying number of divisions and deformed configuration of the clamped cylindrical shell

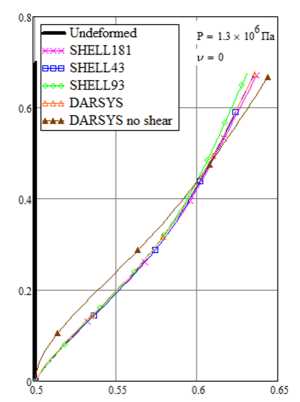
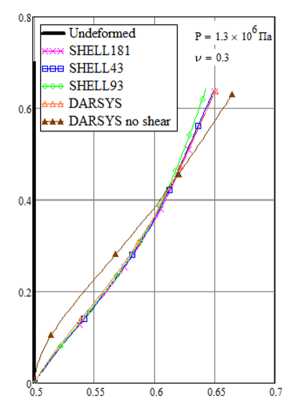
Рис. 8. Влияние учета сдвига при деформировании толстой цилиндрической оболочки

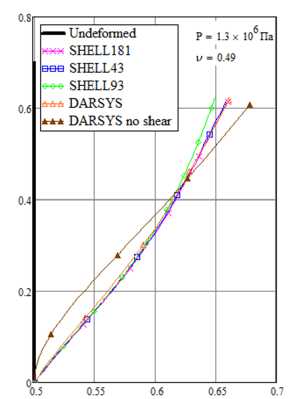
Fig. 8. The effect of shear on the deformed configuration of a thick cylindrical shell

При относительно малых толщинах оболочки влияние сдвиговых деформаций, учтенных формулой (38), мало. Для тестирования работоспособности полученных формул проведем расчет защемленной цилиндрической оболочки с увеличенной в 10 раз толщиной - h = 0,2 м с учетом сдвига и без него. На рис. 8 приведены рассчитанные конфигурации меридиана при давлении P = 1,3 -10 6 Па и разных коэффициентах Пуассона: V = 0; 0,3; 0,49. Из рис. 8 видно, что учет сдвига по разработанным формулам вносит существенный вклад для толстой оболочки и достаточно хорошо согласуется с расчетами в ANSYS. Необходимо отметить, что наилучшую сходимость результатов с ANSYS показали расчеты с коэффициентом коррекции сдвига к = п ² /12 .

На рис. 9 приведены зависимости перемещения верхней точки меридиана в зависимости от давления, рассчитанного разными КЭ ANSYS и в DARSYS по разработанным формулам. Из данных рис. 9 видно, что результаты хорошо согласуются между собой.

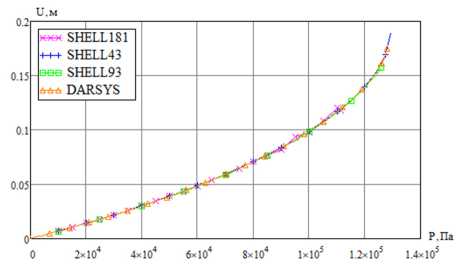
Рис. 9. Зависимость перемещения от давления защемленной цилиндрической оболочки

Fig. 9. Pressure dependence of displacement of the clamped cylindrical shell

Необходимо отметить, что нелинейность графиков на рис. 9 обусловлена не только и не столько геометрической нелинейностью решаемых уравнений, сколько уменьшением толщины и увеличением площади действия внутреннего давления при деформировании.

Сопоставления с ANSYS для линейных уравнений (62) успешно проведены в процессе их разработки, но результаты здесь не представлены.

• 5.    Сферическая оболочка

Рассмотрим задачу о деформировании сферической оболочки радиуса R = 0,5 м под действием внутреннего давления Р . Толщина h = 0,02 м, материал взят из предыдущего примера.

В качестве безразмерного параметра длины удобно выбрать угол между радиус-вектором и осью i_r : 0 < ^ < п / 2, тогда меридиан можно описать так:

• r ( ^ ) = R cos ( ^ ) + 8, z ( ^ ) = R sin ( ^ ) , (65)

где 5 = 10 ¹² <<  R - константа для разрешения численной неопределенности в верхней точке. Краевые условия:

при ^ = 0 : T, r = U_z =Y= 0 ;

при ^ = п /2 : U r = T_2z = y= 0 .         (66)

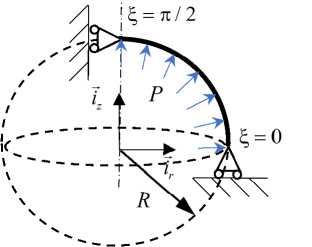
Рис. 10. Сферическая оболочка. Расчетная схема

Fig. 10. Spherical shell. Calculation scheme

На рис. 11 приведены зависимости полного перемещения точек меридиана от числа разбиений (перемещения всех точек равны), рассчитанные с помощью скрипта APDL в ANSYS и по формулам (56)–(61) в DARSYS при значении давления P = 4 - 10 ⁵ Па. На рис. 12 приведены рассчитанные зависимости перемещения сферической оболочки от давления. Из рисунков видно, что результаты хорошо согласуются.

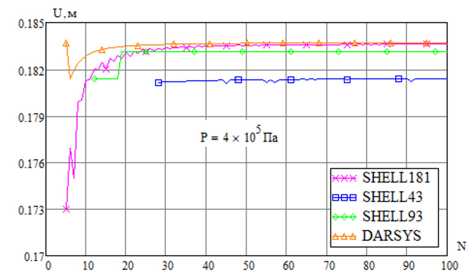
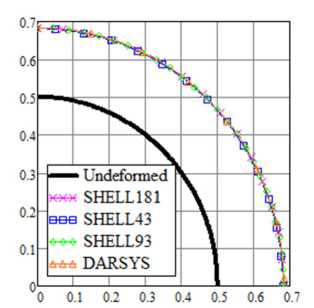
Рис. 11. Сходимость перемещения при варьировании числа разбиений сферической оболочки

Fig. 11. Convergence of displacement when varying the number of divisions of a spherical shell

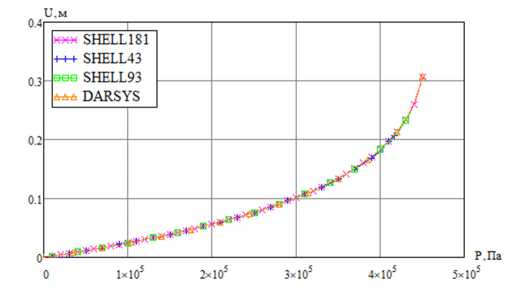
Рис. 12. Зависимость перемещения точки сферической оболочки от давления

перемещения эллиптической оболочки от давления. Из данных рисунков видно, что результаты хорошо согласуются.

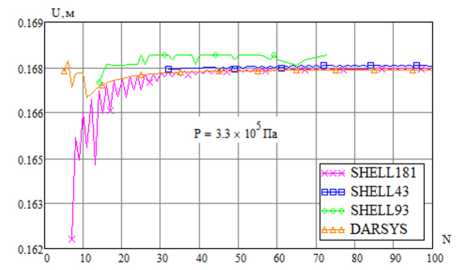
Fig. 12. Pressure dependence of displacement of the spherical shell

• 6.    Эллиптическая оболочка

Рассмотрим задачу о деформировании эллиптической оболочки с полуосями а = 0,4 м, b = 2 а под действием внутреннего давления P (рис. 13). Толщина и материал взяты из предыдущих примеров.

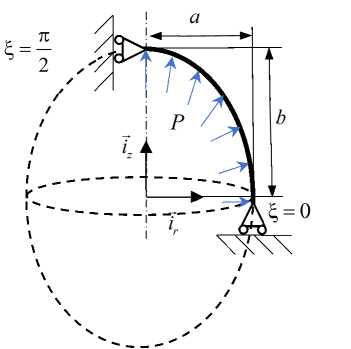
Рис. 13. Эллиптическая оболочка. Расчетная схема

Fig. 13. Elliptical shell. Calculation scheme

В качестве безразмерного параметра длины выбран угол между радиус-вектором и осью i r : 0 <^<п / 2, тогда меридиан можно описать так:

r ( ^ ) = a cos ( ^ ) + 5, z ( ^ ) = b sin ( ^ ) , (67)

где 5 = 10 ^{- 12} <<  R - малая константа для разрешения неопределенности в полюсе. Краевые условия совпадают с условиями для сферы (66).

На рис. 14 приведены зависимости полного перемещения точки меридиана, лежащей на малой полуоси i_r ( ^ = 0) от числа разбиений, рассчитанные с помощью скрипта APDL в ANSYS и по формулам (56)–(61) в DARSYS при значении давления P = 3,3 -10 5 Па. На рис. 15 приведены рассчитанные зависимости

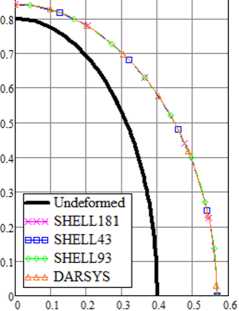
Рис. 14. Сходимость перемещения при варьировании числа разбиений эллиптической оболочки и деформированная конфигурация

Fig. 14. Convergence of displacement with a varying number of divisions of elliptic shell

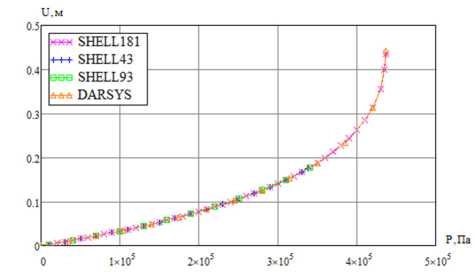
Рис. 15. Зависимость перемещения точки экватора эллиптической оболочки от давления

Fig. 15. Pressure dependence of the displacement of the equator point of the elliptical shell

Необходимо отметить, что предлагаемые уравнения геометрически линейного и нелинейного деформирования, полученные для произвольной параметризации меридиана в отличие от линейных уравнений, полученных в [26], где для задания геометрии эллиптической оболочки пришлось бы привлекать громоздкие формулы связи между длиной дуги и угла, в формулах (56)–(62)

параметризация очень проста в использовании. Кроме того, применение метода конечных разностей в конечном счете приводит к решению СЛАУ с матрицами, которые не содержат параметр ^ в явном виде, следовательно, формулирование исходных данных не требует обязательной записи аналитических формул для меридиана, и они могут формироваться поэлементно, аналогично формированию исходных данных для применения метода конечных элементов.

• 7.    Коническая оболочка

Рассмотрим задачу о деформировании конической оболочки под действием внутреннего распределённого давления P , радиус окружности дна R = 0,5 м, угол конуса ф = п /6 (рис. 16), толщина и параметры материала взяты из предыдущих примеров. Точки меридиана опишем следующими формулами:

• r ( ^ ) = R ^ + 5, z ( ^ ) = R M- , о<^< 1,   (68)

tan ф где 5 = 10-12 << R - малая константа для разрешения неопределенности в вершине конуса. Краевые условия:

при ^ = 0 : Т_г, = U_r = у = 0 ;

при ^ = 1: U r = U_z = у = 0 .           (69)

Здесь необходимо отметить, что обезразмеривание величин в (48), в частности перемещений и длин, можно проводить к единице длины, и не обязательно использовать реальные геометрические параметры, связанные с оболочкой. Поэтому здесь и в других примерах для описания меридиана используются размерные величины длин, а получаемые результаты при выборе разных параметров обезразмеривания длин неразличимы между собой.

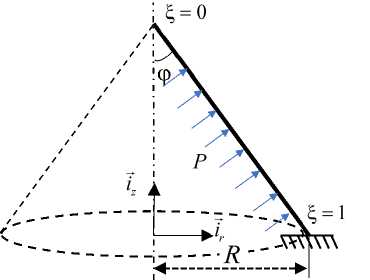
Рис. 16. Коническая оболочка. Расчетная схема

• Fig. 16.    Conical shell. Calculation scheme

На рис. 17 приведены зависимости полного перемещения вершины конуса ( ^ = 0) от числа разбиений, рассчитанные с помощью скрипта APDL в ANSYS и по формулам (56)–(61) в DARSYS при значении давления P = 3,5 • 10⁵ Па. На рис. 18 приведены рассчитанные зависимости перемещения от давления. Из рисунков видно, что результаты хорошо согласуются.

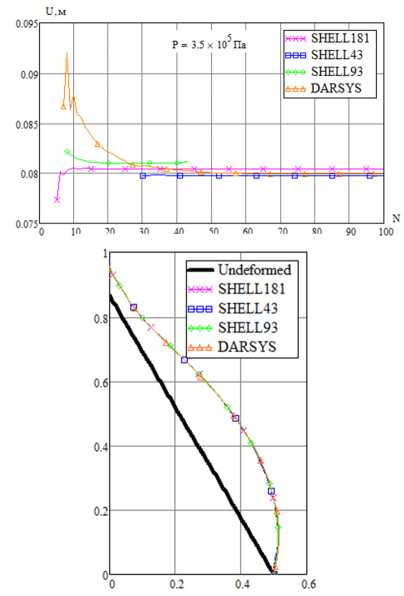
Рис. 17. Сходимость перемещения при варьировании числа разбиений конической оболочки и деформированная конфигурация меридиана

• Fig. 17.    Convergence of displacement when varying the number of divisions of the conical shell and deformed meridian configuration

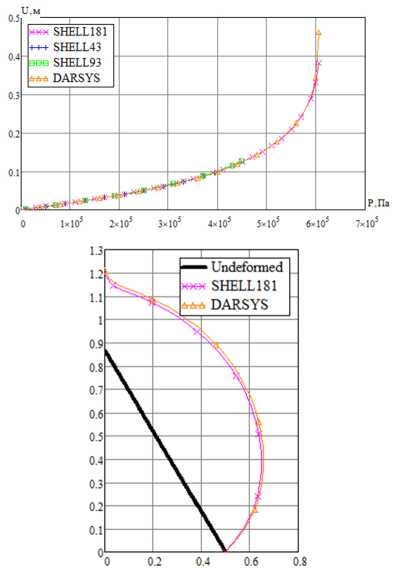
Рис. 18. Зависимость перемещения вершины конической оболочки от давления и деформированная конфигурация при давлении P =6e5 Па

• Fig. 18.    Pressure dependence of conical shell top displacement and deformed configuration at pressure P =6e5 Pa

  8. Составная оболочка

  
  

  Рассмотрим задачу о деформировании составной оболочки под действием внутреннего распределённого давления P , радиус цилиндра R = 0,5 м, высота цилиндра H = 0,8 м, длина образующей конуса L = 0,3 м, ф = п / 6 , толщина и материал взяты из предыдущих примеров. Координаты точек меридиана удобно задать двумя участками на интервале 0 < Ч <  2 следующим образом:

  
  
  

  1.1

  0.9

  0.S

  0.7

  0.6

  0.5

  0.4

  0.3

  0.2

  0.1

  
  

  r ( Ч ) =

  
  

  J R - L sin ( ф )( 1 — Ч ) , 0 <Ч< 1, [ R , 1 <Ч< 2,

  
  

  [ H + L ^cos ( ф )( 1— ^Ч ) ^{, 0}<^Ч< ¹

  z ( Ч ) = 1

  [ H ( 2-ч ) , 1 <Ч< 2.

  
  
  
  

  Краевые условия:

  при ч = 0: T 2 _г = T 2 z = M 2 ф = 0;

  
  

  при Ч = 2: U_r = U_z =у = 0.          (71)

  
  

  Условия стыковки в DARSYS реализованы в автоматическом режиме (достаточно указать точки, в которых есть разрывы функций исходных данных), однако разработанные уравнения могут решаться без стыковки, но это приводит к пилообразному изменению (в пределах погрешности вычислений) рассчитываемого перемещения точки при плавном изменении дискретизации.

  
  
  

  %.1   0.2 0.3   0.4 0.5   0.6   0.7

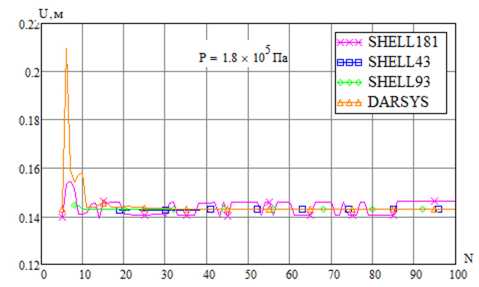
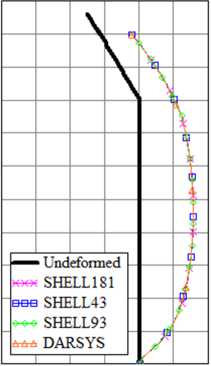
  Рис. 20. Сходимость перемещения при варьировании числа разбиений составной оболочки и соответствующая деформированная конфигурация

  
  
  

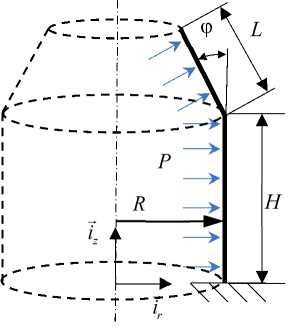
  Рис. 19. Составная оболочка. Расчетная схема

  Fig. 19. Combined shell. Calculation scheme

  
  

• Fig. 20.    Displacement convergence when varying the number of divisions of the combined shell and the corresponding deformed configuration

  

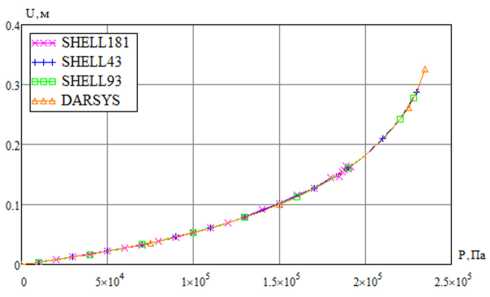
  Рис. 21. Зависимость перемещения верхней точки меридиана составной оболочки от давления

  
  

На рис. 20 приведены зависимости полного перемещения верхней точки меридиана составной оболочки ( Ч = 0) от числа разбиений, рассчитанные с помощью скрипта APDL в ANSYS и по формулам (56)–(61) в DARSYS при значении давления P = 1.8 - 10⁵ Па . На рис. 21 показаны рассчитанные зависимости перемещения той же точки от давления. Из рисунков видно, что результаты хорошо согласуются.

• Fig. 21.    Pressure dependence of the displacement of the upper meridian point of the combined shell

Заключение

В работе представлен вывод разрешающей системы геометрически нелинейных дифференциальных уравнений статического деформирования осесим- метричной оболочки вращения на основе общих уравнений оболочки произвольной формы, записанных в глобальных координатах. Полученные уравнения учитывают большие продольные деформации, поперечных сдвиг, изменение толщины при деформировании, произвольную геометрическую форму меридиана. Уравнения внедрены в собственный программный комплекс по расчету механики стержневых систем – DARSYS, в котором реализован алгоритм численного