Расчет структурных и термохимических констант низших оксидов алюминия

Разработанная ранее математическая модель расчета эффективных ионных радиусов [1] позволила создать их систему [2], согласующуюся с рентгеновскими измерениями параметров кристаллических решеток бинарных и сложных соединений. Модель позволяет определять эффективные радиусы простых и сложных ионов, нейтральных аддендов, структурных фрагментов, параметров кристаллических решеток соединений, формирующихся в кубической сингонии. Адекватность модели экспериментальным (справочным) данным подтверждена согласием с параметрами решеток многочисленных сложных соединений - нормальных и обращенных оксидных, сульфидных, смешанных шпинелей типа 2-3 и 2-4, перовскитов типа 2-4, комплексных аммиакатов с простыми и сложными анионами, комплексов типа K2PtCl6 - всего 164 вещества [3-12].

В модели принято и обосновано деление сложных веществ на фрагменты. В частности, оксидные шпинели типа 2-3 представляются в виде Ме²⁺[Ме³⁺₂О₄] для нормальных и Ме³⁺[Ме²⁺Ме³⁺О₄] - для обращенных. Это дает возможность, используя известные значения радиуса иона А1³⁺ и параметры решетки шпинели А1₃О₄, по предложенной методике рассчитать радиус иона А1²⁺. Для получения достоверных результатов расчета необходимо использовать надежные данные о параметре решетки шпинели.

В литературе [13, 14] для шпинели А1₃О₄, полученной восстановлением смеси А1 + А1₂О₃ углеродом, приводятся значения параметра d = 7,93 и d= 7,915. В то же время путем восстановления корунда монооксидом углерода и последующей конденсации газообразных продуктов восстановления нами получено достаточное количество кристаллического конденсата для проведения разнообразных исследований [15, 16]. В составе конденсата выделены и надежно идентифицированы низшие оксиды алюминия А1₂О, АЮ и А1₃О₄, а также оксиды переменного состава. В частности, анализ изотропных кристаллов с коэффициентом преломления N= 1,7300 ±0,0005 показал, что это шпинель (структурный тип MgAl₂O₄ - Fd3m-8) состава А1₃О₄. По последним 5 линиям рентгенограммы рассчитан параметр кристаллической решетки шпинели d= 8,0827 ±0,0029. Учитывая, что для восстановления был использован газ, а конденсация из газовой фазы позволяет получать наиболее чистые вещества, считаем эти данные более точными и в расчетах использовали величину d (А1₃О₄) = 8,0827 ±0,0029. ________________________ Серия «Металлургия», выпуск 6

В расчетах линейные размеры (d, г_р г,) выражаются в ангстремах (10“⁸см), термические характеристики ^рН, АД й) - в кДж.

Согласно [5, 12] межструктурное расстояние гр (расстояние между центрами фрагментов) шпинели определяется по формуле гР= ad,                 (1)

где а - геометрическая константа, которая включает в себя структурные константы, характерные для октаэдрической (1/4) и тетраэдриче-ской(8/3л/з ) структур.

Поэтому r„ =a-d =---■= d = 0,3849 d.

р 4 3V3

Принимая d= 8,0827±0,0029, получаем

Гр = ad= 0,3849(8,0827±0,0029) = =3,11103±0,00112.

С другой стороны, согласно модели [6]

, Ъд!2* 2А12+ ■Г[А12О4]2-

- Га,2+ +                 2        ’

,ОА12+ ‘ГА12+ Z[A12O4]2^

причем для нормальной шпинели минимальный радиус комплексного иона [А13+2О4]2~ равен 2,17897 [5, 12]. Дебаевский радиус экранирования наружного иона Ме2+ в шпинели г^, r^ = roznS -3>/2 =17,581767-3V2 =74,59312.

Подставляя в уравнение (2) численные значения г, „ ₂- , г„,,₂₊ , г„ и решая его относительно [А1₂О₄] DM ¹

г 2+, получим

74,59312 тА12+ -2,17897

3,11103 = г,2+ +----------^----------,

"   74,59312-^-4,74791

откуда г 2+ = 0,72110 ±0,00112.

Таким образом, исходя из уточненного параметра кристаллической решетки нормальной шпинели d (А1₃О₄) = 8,0827 ± 0,0029 радиус иона ^2+= 0,72110 ±0,00112.

Радиус А1²⁺ может быть рассчитан также, исходя из параметра решетки монооксида АЮ. В [17] приведен параметр кубической решетки АЮ d= 5,67. Согласно [11, 12] радиус катиона А1²⁺ в оксиде с кубической решеткой можно определить из уравнения

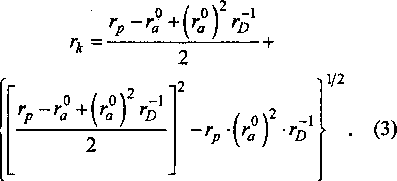
Здесь r^ - минимальный радиус аниона О²'= 1,35806 [1,2,12].

Структурная константа а для АЮ включает в

,                            -               8

себя тетраэдрическую константу —•=, что позво-3V3

ляет предположить формирование оксида в структурном типе ZnS (сфалерит). В этом случае струк турная константа а = —=--= 0,375; дебаев ский радиус экранирования

- о R _ ^rD -^DZaS "     ‘     ~

= 17,581767-272—^ = 76,56241, зТз а гр = a -d = 0,375-5,67 = 2,12625.

После подстановки в уравнение (3) численных величин и решения его относительно г_к получим г ₂₊⁼ 0,72127.

Таким образом, определенная из разных исходных данных величина г ₂+ хорошо согласуется - разница составляет 0,00017 или 0,02%, однако предпочтение следует отдать значению, полученному из параметра решетки шпинели как более надежно определенной исходной величины. По этому значению г _г+ и используя уравнение (2) можно скорректировать параметр решетки АЮ.

1()+.....О^НО-?^!.^

р           0,72110-76,56241-1,844327

Отсюда параметр решетки АЮ d=2,12610 / 0,375 = 5,66960.

Зная величину радиуса А12+ и определив размер аниона [А12+А13+О4]3' из выражения

_ (^Двн ^Ьн)" ^ср "^а

можно рассчитать [5,6] параметр решетки обращенной шпинели А13+[А12+А13+О4].

Радиус иона А13+ равен 0,58917 [12]. Для внутренней сферы [А12+А13+О4] [5, 6,12]:

г„ =-‘к,2₊ +Л_|3+) =—-(0,72110 + 0,58917) = 0,65514.

СР 2 '             ' 2

Заряд комплексного иона

Zcp=l-(2 + 3) = 2,5;

поэтому

^вн = ^_ZnS~(3+73)-T^5= 98,66047.

Для наружного катиона ^=^•3-2(73-1) = 77,22448.

Подставляя в уравнение (4) численные значения ^ф . ^ви» Гон и г° определим г_{[д]2+д]3+О4]}з-

Г[А12+А13+о4]3- =0’ 65514 +

(98,66047-77,22448)-0,65514-1,35806 = 21g52 (98,66047 - 77,22448) -0,65514-1.358062 ’’

Межструктурное расстояние г_р согласно уравнению (2)

■'rA]2+A13+o4f-

Гр = ?А13+ +         1^2

^2^3^ J-=0,58917+2^22^^

77,22448-0,58917-2,218522

Отсюда d= г_р/а = 3,07679 / 0,3849 = 7,99374.

Полученный для обращенной шпинели А1₃О₄ параметр d= 7,99374 также больше приводимого в литературе (<7 = 7,93 и <7=7,915 [17]). Это, возможно, свидетельствует о том, что в шпинели, полученной восстановлением смеси А1 + А1₂О₃ углеродом, присутствовали примеси, сходные по структуре, но с меньшими параметрами решетки, например АЮ.

Результаты расчета геометрических констант кристаллических структур позволяют определить энтальпию образования кристаллических оксидов А/7° и энтальпию их кристаллических решеток &рН. В работе [12] изложена методика расчета, подтвержденная экспериментальными (справочными) данными для 98 соединений (галиды, оксиды, халькогениды, нитраты металлов различных зарядов и кристаллических структур). Согласно этой модели энтальпия образования кристаллических решеток ^рН

A^(MenAm) = АЯ0 + АЯ^. (6)

Здесь А/7₀ - энтальпия нулевого уровня, от которого идет отсчет. Величина Айо постоянна для данного типа кристаллической структуры, зарядов частиц и их электронного строения. \Н_Ю - энтальпия взаимодействия, которая учитывает взаимодействие частиц, их заряд, строение и структуру кристаллической решетки.

Примем, что отсчет ведется от простейших атомов водорода. Тогда

№₀=N_a— -ю-Чо'³-/^).

«о где Na = 6,022045-1023 моль'1 - число Авогадро, е = 4,803242-10'10 CGSE (г1/2см3/2с'’), Ю'8 и 10'3 -численные коэффициенты перевода единиц в систему СИ, а0 = 0,52912-1О'8 см - боровский радиус атома водорода,/^ - функция структуры и заря- да, которая включает в себя структурную константу ^2.........-- и произведение ZK2- Z2, "Z.K и Za- величина зарядов катиона и аниона соответственно.

После подстановки численных значений получим АН₀ = 114,174.

Энтальпия взаимодействия

АНЮ = Na---А^ КЧ-10”8 • КГ3 ■ /2 (Z), где гр = ad - межъядерное расстояние, а - геометрическая константа, d - параметр кристаллической решетки, Ам - число Моделунга, КЧ - координационное число (КЧ= 6),f2(Z) - функция структуры и зарядов, которая включает в себя структурную константу ^(V3+ 1^ и произведение ZK ZQ.

После подстановки численных величин для одно-одно зарядного соединения получим

АЛ = 114Д74-/1® + ¹⁰⁸⁷’⁴¹²⁵. А_м - /₂(Z). (7) ^ГР                 .

В то же время по определению

ЛрН°(МеЛт) = п- A^fMe^) + т- Д//⁰^”^-,) -

-Д^ГМе^кр).           (8)

Уравнения (7) и (8) можно использовать для расчета различных величин. Используем их для определения А/^АЮкр).

Как уже отмечалось, АЮ кристаллизуется по типу ZnS (сфалерит). Следовательно, приведенное число Моделунга для этой структуры Л_м = 1,63806 [18]; г_р = 2,12625. Уравнение (7) в этом случае принимает форму:

ДХ(АЮ) = 114,174-3-

-J087^.1)63^

г                                   г р                                р

После подстановки это дает

ДХ(АЮ)= =811,9032 + 3350,9642 = 4162,8674.

Известно, что ДуН°(А1²⁺_г) = 2728,683 ±4,184 [19]; aX(O²\) = 1069,128 ±0,116 [12]. После подстановки в уравнение (8) численных величин АЛ°(Ме_пА_ш), Д₂Д°(Ме'”⁺_г) и АЛ°(А”~_Г) получаем

Д/ЛАЮкр) = 2728,683 + 1069,128 - 4162,867 = = -365,056.

Возможен и другой метод расчета энтальпии образования кристаллических соединений [20]. При разработке этой модели расчета стандартной энтальпии образования оксидов из работ [21-23] заимствована идея ее зависимости от удельной (на единицу величины заряда ядра) энтальпии Л и от состава, а из оправдавших себя моделей расчета теплоемкости и энтропии [24-25] - идеи о делении поля «состав-свойство» на области твердых растворов, о введении понятия кристаллообразующего компонента и объемной структурной постоянной К.

В модели принимается, что на каждый ядер-ный заряд кристаллического вещества приходится одинаковая энтальпия. Поэтому удельная энтальпия является эффективной величиной и определяется как

-АЛ Ь =—±—

Zz

где ZZ - сумма ядерных зарядов (порядковых номеров элементов) с учетом состава оксида. Это уравнение используется для расчета h анализируемых веществ.

Зависимость h от состава х (х - мольная доля кислорода, приходящаяся на 1 моль металла) можно отобразить линейным уравнением [20]:

h = a + KK4x. (11)

Все поле диаграммы состав - свойство разбивается на области твердых растворов, в которых выделяются кристаллообразующие компоненты. В первой области твердых растворов кристаллообразующим всегда является металл. Поскольку для металла А// =0, то для любой системы зависимость h =f(x) начинается с нуля. В других областях твердых растворов кристаллообразующим может быть принят любой устойчивый оксид, для которого известны состав, структура, энтальпия образования. Поскольку в каждой области К имеет разное численное значение, определяемое сочетанием структурных констант и координационных чисел сопрягаемых на границе областей решеток, то координаты самих границ определяются совместным решением уравнений (11) для соответствующих областей.

В работах [24-25] показано, что в системе Al-О существуют две области твердых растворов, на границе которых находится монооксид алюминия АЮ. Это подтверждается и результатами анализа кристаллических структур оксидов алюминия. Алюминий кристаллизуется в структуре ГЦК (типа Си), А12О - антифлюорит (анти-СаГ2), АЮ имеет кубическую структуру (типа ZnS), А13О4 -типичная 2-3 шпинель (типа MgAl2O4), А12О3 имеет ромбическую (типа а-А12О3 - корунд) или ГПУ упаковку. Граница должна проходить при перестройке структур ZnS в более сложные упаковки, то есть по АЮ.

Анализ зависимостей h-x целесообразно начать со второй области твердых растворов, так как ее внешней границей является хорошо изученный корунд. В работе [25] показано, что в объемную структурную постоянную К входят структурные константы к ГЦК, тетраэдрической и примитивной структур.

В рассматриваемом случае

= —+1 (V6-1) =2,7048.

I 2 ) Х

Координационное число рассматриваемой структуры КЧ= 12. Поэтому во второй области твердых растворов (прих = 1...1,5) уравнение (11) принимает вид:

й₂ = а₂+К₂- 12-х = а₂⁺ 32,4576-х.

Учитывая, что h(Al2O3) = 33,5138 ± 0,0251, из последнего уравнения следует, что а2 = - 15,1726 ±0,0251. И тогда окончательно уравнение (11) можно записать в виде й2=-15,1726+32,4576-х.       (12)

Результаты расчетов по этому уравнению приведены в табл. 1 и на рисунке.

Определение энтальпии АЮ по уравнению (12) позволяет представить уравнение (11) в области твердых растворов х = 0... 1,0 в виде уравнения й, = 17,285-х.               (13)

Отсюда /^(АЮкр) = - 362,985.

Таким образом, двумя независимыми методами расчета получены практически одинаковые значения энтальпии образования монооксида АЮ: - 362,985 кДж/моль и - 362,606 кДж/моль. Поэтому можно принять АуН°(АЮч,) = - 362,796.

Зная А//°(АЮЧ,), можно определить Ар7/0(АЮкр) по уравнению (8), которое в этом случае принимает вид:

A^CAIO,,) = АХ(А1²⁺г) +А₂Д⁰(О²"_г) - А^АЮкр).

После подстановки численных значений получим

А^АЮкр) = 2728,683+1069,128+362,796= 4160,796.

Хорошее согласие величины Ауй°(А1О1ф), полученной из независимых моделей, позволяет рассчитать гДАЮ^,) и сДАЮкр), решая совместно уравнения (8) и (9):

АрЯ°(А1Ожр) = 817,151 + 7108,6202 / г_р откуда г_р = 2,12613 и d = 5,66968. Отличие рассчитанного параметра кристаллической решетки АЮ от приведенного в [17] составляет 0,00032.

Расчет радиуса А1²⁺ по уравнению (3) с использованием уточненной величины т_р дает г ₂₊ = 0,72114. Исходя из вычисленных независимыми способами трех значений г ₂₊ 0,72110; 0,72127 и 0,72114, можно считать, что ^2+ = =0,72117+0,00011; а «/(АЮ^) = 5,66976+0,00011. Численные значения А//°(АЮ,р), ^(АЮ^) и г ₂₊ можно использовать в качестве справочных, поскольку они взаимно согласованы.

Таблица 1

Стандартные энтальпии образования кристаллических оксидов алюминия (кДж/моль)

Вещество	Структура	Известные значения	EZ	Результаты расчета
				h
А1	ГЦК(Си)	0 по определению	13	0	0
А12О АЮо.5	Анти-СаЕ2	Отсутствуют	34	8,6425	293,845
АЮ	ZnS (сфалерит)	364 [26]    .	21	17,285	362,985
А13О4 АЮ1.333	2-3 шпинель (MgAl2O4)	Отсутствуют	71	28,1042	1995,398
А12О3 аю15	ГПУ (корунд)	1675,692+1,255 [19]	50	33,5138	1675,690

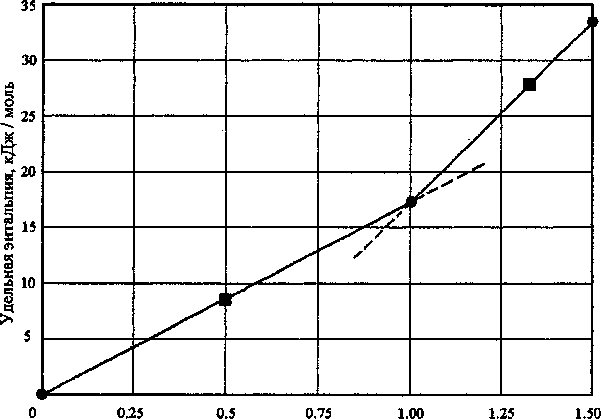
Доля кислорода на один ион металла

Удельная энтальпия h образования кристаллических оксидов алюминия:

• - справочные данные, ■ - результаты расчета

Таблица 2

Результаты расчета ионных радиусов (г) и параметров (d) кристаллических решеток (А), энтальпии образования оксидов и их кристаллических решеток (кДж/моль)

Вещество	r,d	-A/7(Mez+r), -ДДА1ОХЧ>) (справочные данные)	-ДДА1ОХКр)	-^pH
А1	1,43175 [12]		—	—
АГ	0,93036+0,00126 ур.(З) 0,93014+0,00396 ур.(З)	911,991+4,184 [19]	—	—
А12+	0,72110+0,00012,ур.(2) 0,72127, ур. (3) 0,72114, ур.(З)	2728,683+4,184 [19]		—
А13+	0,58917+0,00001 [12]	5473,387+4,184 [19]		—
А12О	4,9894+0,00784 ур(1) 4.9798 ур.(1) 4,98 [14]	Отсутствуют	293,845 ур.(14)	3185,955+4,184 УР-(9) 3191,2309 УР-(17)
АЮ	5,66960+0,00090 ур.(4) 5,67[17]	364 [26]	365,056 ур.(9) 362,985 ур.(14)	4161,811+4,300 [26] 4160,796 Ур(9 и 13) 4162,867 ур.(10)
А13О4	8,08264 +0,00019 7,93 [13] 7,915[14]	Отсутствуют	1995,398 2004,884 УР-(9)	19947,367 ±4,532 ур.(14) 19956,853 УР.(7)
А12О3		1675,692+0,209 [19]	1675,692	15829,850 ±8,816

Полученная величина г ₂₊ позволяет уточнить параметр кристаллической решетки А1₃О₄. Решение по уравнению (2) дает d = 8,08264; что практически совпадает с экспериментальным значением, но существенно сужает доверительный интервал, доводя его до ±0,00019 вместо ±0,00029.

Помимо этого, величины г 2+ и дХ(А13о4ч>) позволяют уточнить и величину энтальпии образования решетки шпинели АрЯ°(А13О4). Исходя из уравнения (8) можно записать аХ(а13о4)=ду/^А!2^) + за/Ла^,) + +4Ау^(О2~г)-Ду/УА^О^) (14) или после подстановки численных значений Д^(А13О4) = 2728,683 + 2-5473,387 + 4 1069,128 --Ау/°(А13О4кр) = 17951,969 - Ау/°(А1зО4ч,).

Из уравнения (12) А//°(А13О4 „) = - 1995,398 (см. табл. 1).

Тогда

ДУ7°(А13О4) = 17951,969 - (-1995,398) = 19947,367.

С другой стороны, энтальпию образования решетки шпинели А13О4 [А12+(А13+2О2"4)] можно определить, используя уравнение (7). В соответствии с моделью [12] объемная структурная посто янная К шпинели 2-3 складывается из координационного числа КЧ= 6, структурных констант ZnS

V3         г kx =—,NaCl к2 =n2, и примитивной к3 = 1. Она численно равна К = (^ + 1)(А2 - ly’-l/S-THT = =6,91920. Тогда по уравнению (8)

аХ(А1зО₄)= 114,174-9-4 +

₊ 1087,4125-1,63 806- 4        ₌

3,11103

=4110,264 + 15846,599 = 19956,853.

Расхождение величин Ау/°(А13О4), полученных по уравнениям (14) и (7), составляет менее 0,05%, что свидетельствует об их достаточно высокой надежности.

Из значения А^ получаем Ду7°(А13О4кр) = =17951,969 - 19956,853 = -2004,884. Полученная величина Ду/°(А13О4 ^ отличается от рассчитанной по другой методике величины АуТ°(А13О4 кр) менее чем на 0,5%.

Используем изложенную методику и для расчета геометрических и термохимических констант оксида А12О. Оксид А12О кристаллизуется с образованием решетки типа антифлюорит и парамет- ром d = 4,98 [17]. Отсюда межъядерное расстоя ние гр = a-d =

V2

— -4,98 = 2,34759. Дебаевский ра диус экранирования для структуры флюорита

15,418081-3,0792 = 47,475377

После подстановки соответствующих численных величин в уравнение 3 получаем г + = 0,93036. Если принять, что параметр (А12О) экспериментально определен с точностью ±0,0025, то г + = = 0,93036 ±0,00126.

Межъядерное расстояние л-^А^О) может быть рассчитано и по уравнениям модели энтальпии кристаллической решетки ЕрН [12]. По уравнению (8) рассчитаем Дрй°(А1₂О)

ДрД°(А12О) = 2Д/7°(А1+Г) + Д^°(О2-Г) - Д/7°(А12О .р) или после подстановки численных значений из [19, 12,26]

ДХ(А12О) = 2-911,991 + 1068,128 + 293,845 = = 3185,954.

Уравнение (7) с учетом Ам(СаЕ₂) = 1,259695 и fj® = 2 • 2 - 2 V2 = 1,171573 принимает форму

Д^= 114,174-1-4 + 1087,412^2596^ ,_1Д71573= ^гр

= 456,696 + 6419,3207/^.      (16)

Отсюда с учетом доверительных интервалов определения компонентов для Дрй°(А12О) Д = ±4,300 получаем гДА12О) = 2,35204 ±0,00370. Следовательно, в соответствии с уравнением (1) d(Al2O) = 4,9894 ±0,00784, а из уравнения (3) г^ = 0,93014 ±0,00396.

Из двух значений = 0,93036 ±0,00126 и г^ = 0,93014±0,00396, полученных независимыми расчетами, получаем г^ = 0,93025 ±0,00043. Используя эту величину, из уравнения (2) получим г_р(А1₂О) = 2,3475, следовательно, t/(Al₂O) = 4,9798.

Эти данные позволяют уточнить ЕрН (А1₂О);

ЕрН (А1₂О) = 456,696 + 6419,3207 / 2,3475 = =3191,2309.

Отличие от ДрЯ (А12О), полученной из Д// компонентов, менее 0,2%.

Выводы

• 1.    Использование уравнений математических моделей расчета эффективных ионных радиусов и энтальпии кристаллической решетки позволили уточнить и согласовать между собой рентгеновские и термохимические данные кристаллического оксида А1₂О, рассчитать эффективный радиус катиона АГ.

• 2.    Вычисления по разработанным ранее моделям расчета эффективных ионных радиусов, энтальпии кристаллической решетки и ■ стандарт

• 3.    Совпадение результатов расчета одних и тех же характеристик по разным методикам и из различных исходных данных свидетельствует об их надежности и достоверности.

ной энтальпии образования кристаллических соединений позволили определить эти характеристики оксидов алюминия А12О, АЮ и А13О4. Полученные данные взаимно согласованы.