Расчет сваи на действие вертикальной и горизонтальной сил

к.т.н.

В районах Севера строительство часто ведется на территориях, имеющих песчаную подсыпку. Здание опирается на сваи из металлических труб и для сохранения мерзлоты понимается над поверхностью подсыпки на некоторую высоту открытого продуваемого подполья. В расчетной схеме для сваи может быть принято: нижним концом она защемляется в вечномерзлом грунте, а верхним - в ростверке здания. Свая проходит подсыпку, мощность слоя которой может достигать 7,0 м и продуваемое подполье (1-1,5 м). Большая длина делает ее гибкой; важное значение приобретает определение сопротивление сваи горизонтальным перемещениям при одновременном действии вертикальной и горизонтальной сил. Решение, приведенное в СНиП [1], предназначено для свай посто- янного сечения и при определении горизонтальных перемещений действие вертикальной силы не учитывает.

В работе [2] приводится решение задачи про-дольно-поперечного изгиба стержня методом конечных разностей. Геометрическая нелинейность учитывается при записи дифференциальной зависимости между внутренними силовыми факторами

5 = -^--A,-tga , где Q, М, N - поперечная сила, изгибающий момент и продольная сила в сечении стержня; а -угол наклона упругой линии к продольной оси х.

В качестве основных неизвестных приняты прогибы стержня Г, в точках j = 1,2,... п, нанесенных на стержне с некоторым шагом И. Условие равновесия участка стержня, выделенного в окрестности рядовой точки /, имеет вид

£ а_ц V, = F,h\j = i-2,i-l,i,i + lJ + 2 . где ay - коэффициенты, зависящие от изгибных жесткостей стержня, которые для каждой точки j могут иметь свое значение, и продольной сжимающей силы N; F, - внешняя поперечная сила, приложенная в точке z.

Для проверки алгоритма был решен ряд задач по определению усилий в опорных связях от еди-

Дано решение о продольно-поперечном изгибе стержня, который защемлен верхним и нижним концами и нижней своей частью погружен в песчаную подсыпку. Работа выполнена в связи с проектированием свайных фундаментов для объектов, возводимых в условиях вечной мерзлоты.

ничных кинематических воздействий при различных значениях продольной сжимающей силы. При шаге точек, равном 1/20 длины стержня, отклонения от точных значений [3], не превысили 1%. Хорошие результаты получились также при сравнении с точными решениями [4]. Решались также примеры на определение критической силы для центрально сжатого стержня. Описанный метод, видимо, может быть применен к расчету сваи.

В работе [5] рассматривается деформирование балки, опирающейся на грунтовое основание и воспринимающей вертикальную нагрузку Осадки основания определяются методом эквивалентного слоя, предложенным Н.А. Цитовичем, который, по мнению авторов, может быть применен и к основанию, неоднородному в плане. Равномерно распределенная вертикальная нагрузка, действующая на поверхности основани, определяется формулой

5 = pm_vh₃, где р - интенсивность нагрузки; ш„ - коэффициент сжимаемости грунта; h₃ - мощность эквивалентного слоя.

Если загруженная площадь имеет вид прямо- угольника, то

И_Э = ЬА_Ю,                  (1)

где b - ширина прямоугольника; А_щ - коэффициент эквивалентного слоя.

Величины А_м могут быть взяты из [6, табл. 11.4] в зависимости от соотношения сторон прямоугольника и коэффициента поперечной деформации грунта v₀.

Для системы «балка-основание» приняты следующие предпосылки: балка деформируется по закону гука; справедлива гипотеза плоских сечений Бернулли; вертикальные перемещения балки и поверхности основания тождественны; действие касательных сил на подошву не учитывается.

Задача решается методом конечных разностей. В качестве основных неизвестны принимаются вертикальные перемещения балки и поверхности основания в точках, намеченных с шагом h по длине балки. Для каждой точки i рассматривается ряд загруженных площадей прямоугольной формы с центром в точке г. Ширина всех площадей одинакова и равна ширине балки, длина / = А, Зй, 5/1,..., т.е. / = (1 + 2ти)й, т = 0, 1,2, .... Мощности эквивалентного слоя, соответствующие каждой из этих длин, обозначаются через h_m (по значению т). Осадку, возникающую в точке / от нагрузки, распределенной по площади длиной h в

Экспериментальные исследования

окрестности точки i+m (рис. 1), можно определить по формуле

Si,i+m " ^ФР1+т^ФФг ~ ^m-1),         (2)

где p_i+m- интенсивность нагрузки в точке z+m. Когда основание слоисто по глубине, формула (1) записывается в виде

Р^тЛ2^

Таблица

Пока затель гиб костиt Сила F, мН Перемещение, см Моменты, мНм Реактивные давления, мН/м' 2 4,0 1,108 1,108 7,884 8,462 0,293 0,266 10 3,0 1,116 1,155 3,942 4,222 0,340 0,322 где тч, hj - коэффициент сжимаемости и мощность у-го слоя; Zj - расстояние от середины у-го слоя до низа сжимаемой толщи, в качестве которой берется 2Лэ.

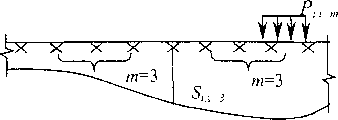
Рис. 1. К определению осадок основания

При этом важно, чтобы суммарная мощность слоев в выражении (3) была равна сжимаемой толще, которую предлагается определять усреднено по формуле

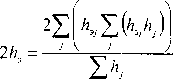
где h_3J - мощность эквивалентного слоя, определенная по характеристикаму-го слоя.

Когда основание неоднородно по площади, формула (2) заменяется усредненной формулой

/        -   f+]            — z+m-l i+m с +2с   +... + 2с   + с

_ 01,1*т

2т в которой s,,+m'         осадки- определяемые по формуле (2) при характеристиках грунта, взятых в точках 1, z+1, ....

Для проверки алгоритма расчитывались балки на однородном основании с модулем упругости Дуб О МПа и коэффициентом поперечной деформации vo=O,3. Сравнение производилось с решением для балки на упругом полупространстве по М.И. Горбунову-Посадову [7]. В частности были расчитаны две балки одинаковой длины 18 модальное и ширины 2 модальное, нагруженные со-средоточеной силой F в середине, имеющиепока-лЕ0а3Ь затели гибкости г - ~   27”, равные 2 и 10 (а -

2(1-v0 )£/ полудлина, 6 - полуширина балки). Получилось хорошее совпадение эпюр перемещений, изгибающих моментов и реактивных давлений со стороны основания. В таблице приводятся значения этих величин для середины балки: в числителе -по Горбунову-Посадову, в знаменателе - по описанному алгоритму.

На основе описанных алгоритмов выполняются расчеты свай на совместное действие вертикальной и горизонтальной сил. Расчетная схема показана на рис. 2.

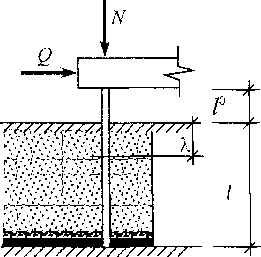
Рис. 2. Расчетная схема сваи: /о - высота подполья; /- мощность слоя подсыпки