Расчет температурно-силовых характеристик в зоне абразивной обработки резиновых покрытий

этом линии L 2 и L 3 соединены частью окружности L 4 с радиусом, равным радиусу скругления режущей кромки на абразивном зерне. Область R представляет собой фрагмент резинового покрытия, находящийся в области контакта с абразивным зерном.

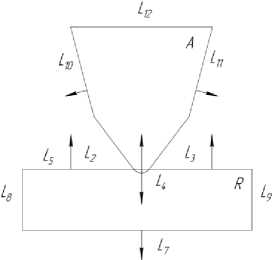
Рис. 1. Расчетная схема для определения распределения температуры в зоне абразивной обработки

Предполагается, что в процессе вращательного движения абразивного круга при механической обработке покрытия в зоне контакта происходит циклическое возникновение теплового потока, продолжительность действия которого определяется временем контакта зерна с резиновым покрытием t r , после чего зерно выходит из зоны контакта и находится вне зоны воздействия теплового потока до момента окончания i -го цикла t ц i перед очередным контактом зерна и покрытия. Уравнение нестационарной теплопроводности для абразивного зерна и резинового покрытия имеют вид:

5 ² T ( x , у , t ) 5 ² T ( x , у , t ) _      5 T ( x , у , t )

5x2            бу2          'Р'     5 t t > 0; (x, у )е A;

5 ² T ₂ ( x , у , t )    5 ² T ₂ ( x , у , t )           5 T ₂ ( x , у , t )

5 x ²              5 у ²            2 Р 2       5 1     ’

t > 0; (x, y )g R, где T1, Т2 – температура (здесь и далее индекс «1» означает принадлежность к абразивному зерну, индекс «2» к резиновому покрытию), с1, с2 – теплоемкость, с1=930 Дж/(кг·К), с2=1900 Дж/(кг·К); ρ1, ρ2 – плотность, ρ1=3,9·103 кг/м3, ρ2=1,2·103 кг/м3.

Задача определения температурного поля в зоне контакта при абразивной обработке решалась в двумерной постановке, при этом было принято, что размеры областей A, R в направлении z равны единице. Граничные условия, отражающие выделение теплового потока q на линии контакта абразивного зерна с покрытием вследствие трения, имеют вид:

K 1

^д T 1 ( x , y , t )

-------l

a T 1 ( x , y , t ) a ,;      l’j

+ h 1 [ T 1 ( x , y , t ) - T c ] = 0;

t > 0; ( x , y ) g L ₂ , L 3 , L 0 ,L _n, L ₁₂ ;

Гд T ( x , y , t ) ,      d T ( x , y , t ) , 1 , г /      \ i

^K 2      d x      I xLj ⁺      I ,       ^ly^Lj ⁺ h 2 [ ^T 2 ⁽ x , y , t ^{) - T}c ] = ^0;

t >  0; ( x , y ) g L ₅, L ₆;

Гд T(x , y , t)         д T(x , y , t)      1

^K 2 [ ^{2 (} Эх   ) • ^l xL 7 +    ^{2 (} dy    ) • ^l ,L 7 J + h 3 [ ^T 2 ( x ’ У ’ t ) - ^T c 1 = ⁰ ;

t >  0; ( x , y ) g L ₇;

K 1

K 2

K 1

K 2

d T ( x , y , t )

дx д T2 ( x, у , t ) дx

" ^lx 1 ⁺

• ^l x 2 ⁺

a T ( x , y , t )

л         • l y ¹

дy a T2 (x, y, t)

д         • ly 1

a y

+ q = 0;

+ q = 0;

t _щ < t <  t ц + t r ( 1 <  i <  N ) ;

( x , y ) g L₄;

^{д T} 1 ( x , y , t )        a T 1 ( x , y , t )

^          x 1^

дxд д T2 (x, y, t)       д T2 (x, y, t)

•+ x 2 дx

y 1

' y 2

= 0;

= 0;

t _щ + t r <  t <  t цу + 1 ) ;

( x , y ) g L ₄,

где l x 1 , l y 1 – направляющие косинусы нормалей к линии L 4 , направленные внутрь области А ; l x 2 , l y 2 – направляющие косинусы нормалей к линии L 4 , направленных внутрь области R ; t ц i – время начала i -го цикла контакта абразива с резиновым покрытием, t r – время контакта в каждом цикле ( t r = const).

Тепловой поток q , выделенный в результате трения зерна и покрытия на площадке единичной ширины, след которой представлен линией L 4 , характеризуется следующим выражением:

q = τ v (7)

где τ – максимальное значение контактных напряжений от сил трения на линии L 4 , определяемое из соответствующей контактной задачи теории упругости при заданном усилии прижатия абразивного круга, τ=1,77 МПа; v – окружная скорость абразивного круга, v =4,52 м/с. Время взаимодействия зерна с покрытием составляет t r =0,0083 сек; время одного оборота абразивного круга t ц = t ц i +1 – t ц i (1≤ i ≤ N )=0,125 сек. Условия теплообмена с окружающей средой на границе областей A и R :

где l xLj , l yLj – направляющие косинусы внешней нормали к линии L j , h 1 , h 2 , h 3 – коэффициенты теплоотдачи, h 1 = h 2 =130 Вт/(м∙К), h 3 =30 Вт/(м∙К).

При решении задачи принимается, что теплообмен на линиях L 8 , L 9 отсутствует.

д T2 (x, y, z)        д T2 (x, y, z)     _ дx       xLj^     ду       yLj;

t > 0; ( x , y ) g L , L

Начальная температура рассматриваемых областей составляет T 0 =20⁰С:

Т 1 ( ^x , У ^,0 ) = ^T 0     ( ^x , У )^g a              (12)

T ₂ ( x , y ,0 ) = T_o      ( x , y ) g R

Задача, описываемая выражениями (1)(12), решалась методом конечных элементов с использованием программно-вычислительного комплекса ANSYS. Результатом вычислений является определение контактных напряжений τ от сил трения при взаимодействии абразивного зерна с покрытием при условии, что рабочая температура абразивного зерна не должна превышать 100-1200С. Результаты расчета температуры на границе зерна и покрытия при найденном значении τ в процессе абразивной обработки приведены на рис. 2, 3.

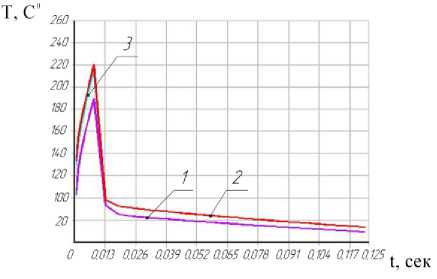
Рис. 2. Зависимость температуры на границе зерна и покрытия от времени при абразивной обработке покрытия:

1 – график температуры зерна вблизи границы зерна и резины, 2 – график температуры на границе зерна и резины, 3 – график температуры резины вблизи границы зерна и резины

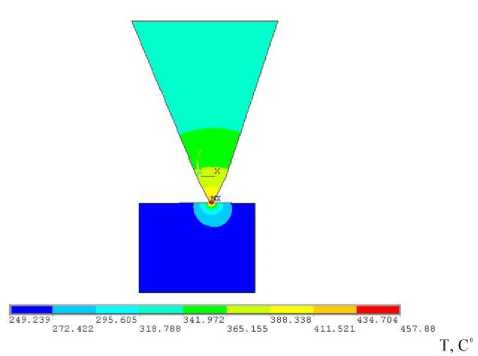
Рис. 3. Распределение температуры в зерне и поверхностном слое покрытия при t=5,47 сек

Вывод: полученные результаты позволяют оптимизировать режимы обработки при заданной скорости вращения абразивного круга посредством изменения усилия его прижатия к обрабатываемому покрытию.