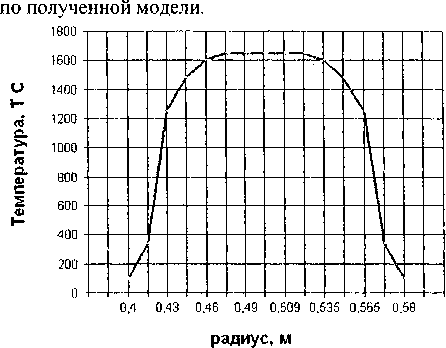
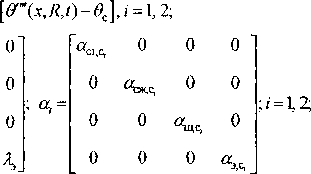Расчет температурных полей в полых слитках при электрошлаковом переплаве

Одним из перспективных направлений производства труб большого диаметра для особо ответственных трубопроводов является изготовление их из полых слитков путем раскатки. Полые слитки из нержавеющих и плоходеформируемых сталей производятся электрошлаковой технологией в специальных печах с двумя кристаллизаторами (внешним и внутренним). При раскатке таких слитков очень важно, чтобы стенка полого слитка была однородной структуры, не содержала дефектов в виде расслоений, наплывов и т.д. Поэтому при наплавлении слитка методом электрошлаково-го переплава (ЭШП) требуется строго выдерживать комплекс технологических параметров - ток переплава, глубину ванны, температуру охлаждающего теплоносителя и др. Поэтому для оперативного управления процессом наплавления слитка, оптимизации в данной работе рассматривается задача по разработке математической модели теплофизических процессов печи ЭШП с двумя кристаллизаторами. В работах [1] и [2] рассмотрена подобная задача, но с одним кристаллизатором.

Печь ЭШП с внутренним и внешним водоохлаждаемыми кристаллизаторами схематично изображены на рис. 1. В коаксиальном зазоре между кристаллизаторами наплавляется слиток. Расходуемые электроды (восемь штук) равномерно распределены в коаксиальном пространстве печи. Диаметры кристаллизаторов внешнего и внутреннего, соответственно равны 580 мм и 400 мм. Качество металла в слитках вторичного переплава во многом определяется направленной кристаллизацией, управление которой представляется возможным путем изменения теплофизических условий.

Рис. 1. Схема печи ЭШП для получения полого слитка в разрезе

Математическое моделирование теплофизических процессов и рассматривается в данной работе.

Печь со сплошным слитком была симметрична относительно оси А, поэтому было три дифференциальных уравнения в системе, описывающих связь между соответственно: вода, стенка и /-й слой, где / = 1, 2, 3,4; 1 - слой слитка твердого, 2 -слитка жидкого, 3 - шлака, 4 - электрода. Печь с полым слитком симметрична относительно оси В, поэтому система состоит из пяти дифференциальных уравнений энергии, описывающих связь между средами соответственно: вода внешнего слоя (в0, стенка(С1), z-й слой, стенка(с2) и вода внутреннего слоя (в2).

При выводе уравнений приняты допущения: теплофизические параметры воды, стенки кристаллизатора, электрода, слитка не зависят от температуры, отсутствует диссипация энергии. Теплообмен аппарата ЭШП с внешней средой отсутствует. Ввиду цилиндрической формы печи ЭШП рассматривается осесимметричная задача.

Итак, с учетом принятых допущений, уравнения энергии для области D_x = {х, Г. 0 <  х < z, 0 <  t < /^} запишем в виде:

— В, К -Л +КС|       ) + а— cbBi \ В1 С1 / СЬСТ\ ст С1 / С1 ^.2

^+ист^=кпс(ес X-Х X-xV

^ ст ^ ст,С|х С1 ст/ ст,с2 \ с2 ст/ аХ   (1 аеп аХ)

Эх       (г drdr )

~ ^=2,02 (УВ2 ~ ^2 ) + ^С2,СТ (^СТ “ УС2 ) + «с2^

80В1 XА

ХГ Х^ ^^В2-^С2 ^^С2 " ⁰⁸²) ⁺ ^ 1?"'

Di = {х, t: z <х< р, t > 0}:

2& 7 А 7 А ⁸ X —^-=к „ (0 -0_С \+к_с „Х-е_с +п.—s 01 ^СЬ^В1 \ ^В1 ^С1 / ^СЬ^СТ\ ^{ст С}1 / ^С1 ^2

^L + t?          (0 -0 U di Sy             ci с 10_ — 0С ) + я —5—I-             1;

• ^{2    v 2} ' Эх              or Эг )

• 80.        7 А 7 А ^дХ

• 80.    ао. ,       , аХ

g_t “ ^=2,=2 (^=2 ~ ^₂) ⁺ X.™ X* ~ ^2 ) ^{+ а}=_г XX’

~ ^и=2      “ Х.=2 (^У=2 “ ^В₂ ) + ^aB₂ -.2 ■

D₃ = {x, t: p < x <  d, t> 0}:

3OB 99,          /         \

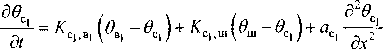
= ^,ш (уш - eC|)+кСъШ (уш - УС2)+ at ох 1 х                       х ’

+а 5Х+Й + ох          or or )

—^- = К_{С в} (ft -ft Jft-ft | + а_с —

Ql ^с2.^в2\ ^в2 ^с2 /     ^с2-™\ ^{ш с}2 / ^с2 ^^2 ’

Э0Вз 90в/ X

----±О_В --- ” ⁼ К. , (ft -ft ) + 22

I St 82 Эх B2> Л 222

8X

Ds, —{x, f. d0}: dft 69.         ,        .6

di ⁸¹ Эх ^{81 c}‘ ^{812    81} 5x² '

dft / x / x ^Ч —— = K. „ (ft -ft )+Kc 3 ft-ft ) + ac —4 gf C1.B1 \ B1 cl/ cl.3\ 3 cl/ C1 ^2 ’ gt 3 gx э-с1 \ С1 э/ 3’C2\ =2    3/ аЧ (\Э9Ч дгбД +д ----3 4- Q--i +----3 .

• ³    Эх² ^r dr Эг² )

• —^ = K_C „ (ft -ft ) + ^_c M-6_C ) + ц. —4; g[ ^C2=^B2\ ^B2 ^c2 /     ^c2’³\ ^{3 c}2 / ^B2 g^T ’

Начальные условия:

0 (х,г,0) = ф (x,r), ф =^_B]>%₂,%_i,p_C2,

r_t2; Z(O,r) = Z_o, Z_o = [0,0,0,Z(r)f;

A(O,r) = Ao, Ao=[O,O,O,A(r)f, на подвижной границе фазового перехода слиток твердый - слиток жидкий ричх = /_ [eCT 0 - о, /)]х - лсж [есж (z+о.г)^, на подвижной границе шлак - электрод /7,4, =/-ЧЧН3 + А-М], ~ЧеЧ + А + ,и .

Условия на границах областей D,:

ft(0,r,0) = rro;

Z Г Г                                    "1^

9(0,г,1) = у(гДхр =^_Bi,y/_B2,y/_Ci,y/_C2,iy_CTJ ;

0‘4i,r,t) = 0; 4, [^(Ол,/)], = a_n,_Ci [9_a(0,r,t) - в,, ], i = 1,2;

ycr(z-0,r,/) = 6'CBt(z + 0,r,/) = rnjl;

6СЖ(Р,М) = ТШ;

y;(x,r„/) = [0], ^(x,r2,0 = [0], ft = [0CT,9„,^,e3f;

6"

6_m(P ^{+ &}- Oft.O = 6₃(p + A + 0,r,0 = r_m; Q = iX;

op. (У_{з +} 273)⁴-(5_{с +} 273)⁴. a_jP1

• PAT. 03-9c           J p,c,S,

В уравнениях приняты обозначения:

индексы вь в2, С], с2, ст, сж, ш, э у соответствующих параметров относятся к воде, стенкам, слитку твёрдой фазы, слитку жидкой фазы, шлаковой ванне, электроду; / = 1, у = ст; / = 2, ; = сж;

i = 3, j = ш; / = 4, j = э ;

• У_В1 > 9_Ч - 9^ , в_С1, 9_СТ, 0_СЖ , 9_Ш, 9₃ - соответствующие температуры сред, °C;

р,, с„ X;, а, - соответственно плотность, кг/м³; удельная теплоёмкость, Дж/(кгтрад); теплопроводность, Вт/(м-град); температуропроводность z-й среды, м²/с;

а_у, р„ Si - соответственно коэффициент теплоотдачи между /-й и j-й средой, Вт/(м²трад); периметр раздела, м; площадь поперечного сечения z-й среды, м²;

Г, - скорость движения z-й среды, м/с;

• х, г, 1, г, К,р - соответственно текущие координаты по длине, м; радиусу аппарата, м; время, с; координата подвижной границы в слитке, м; координата подвижной границы в электроде и граница между электродом и жидкой ванной, м;

Т™ Т_ш - соответственно температуры плавления и шлаковой ванны, °C;

q - теплота кристаллизации, Дж/кг;

Ф,, у,, - известные распределения температур по соответствующим координатам;

m - номер коаксиального слоя для слитка;

<т - коэффициент лучеиспускания.

Термодинамические соотношения, замыкающие эту систему, такие, как зависимость коэффициента теплоотдачи от режима течения воды, коэффициента излучения и др., взяты из экспериментальных данных, полученных разными авторами.

Системы уравнений (1)—(4) решены численными методами с использованием метода конечных разностей.

На рис. 2 приведены некоторые результаты расчетов температурного поля в шлаковой ванне

Рис. 2. Распределение температуры в коаксиальном зазоре для шлаковой ванны при ц=0,4 и г2=0,58 для времени f = 2,5 ч по радиусу

Суров А.Н., Потапов В.И., Бугаев М.С.

Решение систем (1)-(4) позволяет определять температуру в процессе ЭШП в любой точке аппарата и в каждый момент времени.

Полученная в работе математическая модель тепловой работы печи ЭШП может быть основой разработки системы управления вторичным переплавом с целью экономии электроэнергии и повышения качества металла.