Расчет теплофизических свойств кристаллов инертных газов по упругим константам

Полуэмпирические методы, рассматривая разного рода модели взаимодействия между атомами в кристаллической решетке, и используя понятия ион и диполь, позволяют увидеть физическую картину формирования конкретных акустических и оптических мод. При такого рода подходах становятся более физически прозрачными, в частности, механизмы сегнетоэлектрической неустойчивости и электрон-фононного взаимодействия.

В работах [5 – 8] в адиабатическом приближении была построена динамическая модель для ОЦК и ГЦК кристаллических решеток, использующая силы межатомного взаимодействия, имеющие Ван-дер-Ваальсовскую природу. Разработанные математические методы позволили произвести расчеты дисперсионных кривых, фононных спектров, температурных зависимостей теплоемкости и среднеквадратичных смещений для ряда элементов 1 – 5 групп таблицы Д.И. Менделеева, без подгоночных параметров. Исходными данными для этого служили значения упругих констант, атомная масса и параметр решетки соответствующего вещества. При этом обнаружилось достаточно хорошее соответствие экспериментальным данным.

Реализация построенной модели применительно к инертным газам предполагает наличие данных по упругим константам. В работе [9] такие данные получены путем использования комбинированного потенциала Леннарда-Джонса. На основе этих данных в работе [10] произведены расчеты дисперсионных кривых, фононного спектра, температурной зависимости теплоемкости и среднеквадратичных смещений атомов для кристалла инертного газа Ar. В статье [11] приводится зависимость экспериментальных значений модулей Бирча от давления в интервале 0–8 ГПа для Kr, что позволяет по известным формулам найти значения упругих констант. В работе [4] проводилось исследование сжатых кристаллов инертных газов Ar, Ne, Kr, Xe в модели Толпыго, явно учитывающей деформацию электронных оболочек. На основе проведенных расчетов фононных мод для определенных точек зоны Бриллюэна были построены дисперсионные кривые для всех указанных инертных газов при сжатии AV/V0 — 0,7 . Это позволяет по значениям дисперсионных кривых на границе зоны Бриллюэна вычислить упругие константы для Ar, Ne, Kr, Xe при указанном сжатии.

В настоящей работе, исходя из полученных данных по упругим константам для КИГ, рассчитаны дисперсионные кривые и кривые температурных зависимостей теплоемкости для Ar, Ne, Kr, Xe при сжатии A V/V o — 0,7 . При этом обнаружилось хорошее согласие с соответствующими данными, приведенными в работах [1, 3, 4]. Для КИГ Kr рассчитаны дисперсионные кривые при давлении 4 ГПа, а также температурные зависимости теплоемкости в интервале давлений 0–8 ГПа.

1. УРАВНЕНИЕ ДИНАМИКИ ГЦК РЕШЕТКИ

Рассмотрим моноатомную ГЦК кристаллическую решетку и обозначим через д - массу остова каждого ее атома, через q – его заряд, и пусть р — q ² / 4ле ₀ .

Представляя кристалл, имеющим форму куба, зададим в пространстве систему кристаллографических координат Oxyz с единичными векторами е x , е y , e z координатных осей, направленными вдоль соответствующих ребер куба так, чтобы положение каждого узла D — D ijk решетки могло быть задано по формуле:

^ODjk ^— ^С i e x ⁺ j e y ^{+ k e} z ) , (1) где i, j, k G N — {1,2,...,2 n} . Обозначим через д подмножество в n ³ , образованное всеми такими наборами ( i, j, k ) , для которых формула (1) определяет узел решетки. Тогда

Д — {( i, j, k ) G N ³ S сумма i + j + k нечетная }.

Для каждого ^ — ( i , j , k ) E Д обозначим через A ^ атом решетки, положение равновесия которого находится в узле D ; , а через и ^ - смещение остова атома а ; из положения равновесия в некоторый момент времени t . Обозначим, далее, через S 1 ( f ) - множество индексов из Д , нумерующих ближайшие соседние к а ; атомы решетки.

Рассмотрим атом Аг - соседний с атомом Аг. Перемещение остовов атомов а; и а;' относительно друг друга вызывает изменение степени перекрытия орбиталей их внешних электронных оболочек, в результате чего у этих атомов наводятся противоположно направленные дипольные моменты. Пусть е^' - единичный направляющий вектор вектора Df D f-, а w f — Uf — Uf - вектор относительного перемещения остовов атомов А f и А f. Обозначим через r f- — е ff- < е f-, w ^f > - радиальную, а через т f — w^ — r f - тангенциальную состав— — w ff. Тангенциальная ляющие вектора w

составляющая т w может быть разложена на два 1            2                               1

слагаемых т f и т f , где вектор т f направлен вдоль одной из координатных осей, а вектор т¹ ^ ортогонален векторам r f- и т ff . Будем считать, что плечо дипольного момента, p г у , наведенного в атоме А со стороны атома А выражается формулой

1                 2

Р f ' ^К 1 r ^r f ' ^{+ К} 1t ^т f ' ^{+ К} 2t ^т § f ,      ⁽²⁾

где к r , К t , К t - числовые параметры, постоянные для данного кристалла.

Плечо p^ полного дипольного момента, наведенного в атоме А , вычисляется путем суммирования по всем соседним атомам:

^p § ^— Z ^p %

5' G S 1 ( f )

Как было показано в работах [5, 8], в состоянии термодинамического равновесия уравнение движения остова атома принимает вид

Р    Р X д 5——-p ——- Z p f а        а fG S1( f)

где а - поляризуемость атома.

Положим 7 1 _r — Рк 1 _r / а , <7 1 t — Рк 1 t / а , 7 2 _t — вк 2 t / а . Учитывая свойство центральной симметрии кристалла, сумму в правой части уравнения (4) можно представить в виде

Z p f’= Z ⁽ p f '⁺ p ff ) f G S 1 ( f )        f G S 1 ( f )

где G S ₁ ( ) - мультииндекс, нумерующий атом, симметричный к атому А f относительно атома А , а S ₁ ( ) - множество мультииндексов, нумерующих какую-либо полусферу п ервой координационной сферы. Множество S 1 ( f ) естественным образ о м распа д ается на три составляющих: S 1 x ( f ) , S 1 y ( f ) , S 1 z ( f ) , например, первая из которых, нумерует атомы, лежащие в плоскости (100), ортогональной оси Оx . С учетом формул (2), (5) и введенных обозначений уравнение (4) может быть записано так

Hu!; — Z 17 r —°2-1) < ef( wf'+ w«') > ef'+ 711(W5, x + wfx ) ex fG S1 x f)’

^{+ 7} 2 1 ⁽⁽ w ff , y ^{+ w} ; f , y ) ^e y ^{+ (} w ff , z ^{+ w} ; f , z ) ^e z ^{)] +}

+ Z 17 r — °21) < ef(wf'+ wf) > ef'+ 711(Wfr, y + Wfy ) ey + fg S1 y (a’

^{+ 7} 2 1 ⁽⁽ w ff , x ^{+ W} ff , x ) e x ^{+( W} f z ⁺ wfyzz ) e z ^{)] +}

⁺ Z [ ⁽ ° 1 r ^— ° 2 1 ) <  ^e f ⁽ w f ⁺ w f ) >  e f '^{+ 7} 11 ⁽ w f z ⁺ W f- z ) e z ⁺ f G S 1 z f )

^{+ 7} 2 1 ⁽⁽ W f x ^{+ W} f x ) e x ⁺⁽ W f y ^{+ W} f y, ) e y ^)]

Решая уравнение (6) в континуальном приближении приходим к равенствам [8]:

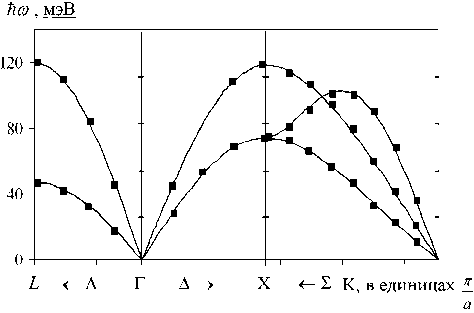
Рис. 1. Кривые дисперсии фононов в Ar при сжатии A V/V q - 0,7

° 1r = -( С „ + С ₁₂ + С 44 ) ,

° 1 1 = -(2 С 44 - С 11 ) ,

° 2 t ^- 4^{( С} 11   ^С 12   ^С44 ) .                (7)

В общем случае, как показано в [8], уравнение (6) сводится к однородной системе:

axgx + bzgy + bygz - МЮ2gx , bzgx + aygy + bxgz - МЮ2gy ,         (8)

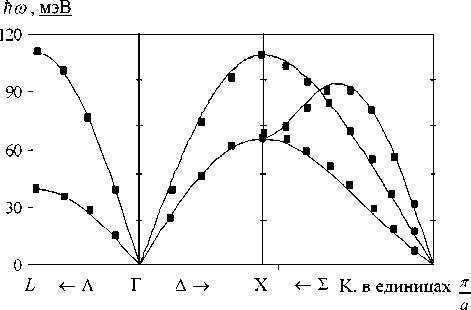
Рис. 2. Кривые дисперсии фононов в Ne при сжатии A V/V q - 0,7

b y g x ⁺ b x g y ⁺ a z g z ^- М ^{Ю 2} g z , позволяющей по волновому вектору

2л .

K - —(kx e + ky e + kz e) xx yy zz na из первой зоны Бриллюэна определить частоту Ю и направления вектора поляризации g - gx ex + gy ey + gz ez каждой из трех колебательных мод. Показано, что коэффициенты динамической матрицы выражаются формулами: ax - 4°1 (1 - c(ky )c(kz )) + 2(°1 r + °21 )(2 - c(kx )c(kz ) - c(kx )c(ky ):, bx - 2(°1 r - °21 )5(ky )5(kz ) ,

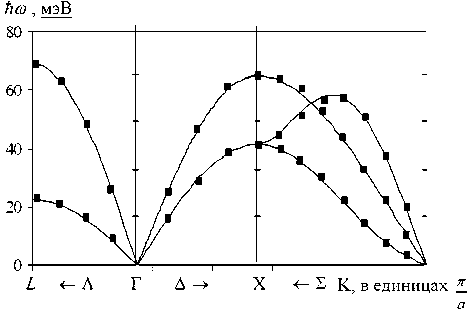
Рис. 3. Кривые дисперсии фононов в Kr при сжатии A V/V q - 0,7

где c ( k ) - cos ^ k , 5 ( k ) - sin ^ k . nn

В настоящей работе в результате решения системы (8) и ее характеристического уравнения для всех допустимых значений волнового вектора с учетом равенств (7), построены дисперсионные кривые для основных кристаллографических направлений и рассчитаны температурные зависимости теплоемкости КИГ: Ar, Ne, Kr, Xe. Дисперсионные кривые и температурные зависимости теплоемкости для указанных КИГ приводятся в сравнении с данными работ [1, 3 – 4] при сжатии A V/V q - 0,7 .

Ниже на рисунках 1 – 6 приведены дисперсионные кривые и температурные зависимости теплоемкости, рассчитанные в рамках предложенной модели для КИГ: Ar, Ne, Kr, Xe при сжатии A V/V q - 0,7 в сравнении с данными работ [4], [1, 3] соответственно (данные других авторов нанесены точками). Как можно видеть, и те, и другие кривые имеют хорошее согласие. На рис. 7 – 8 приводятся дисперсионные кривые для КИГ Kr при давлении 4 ГПа, а также температурные зависимости теплоемкости в интервале давлений 0– 8 ГПа, рассчитанные на основе экспериментальных данных для модулей Бирча [11].

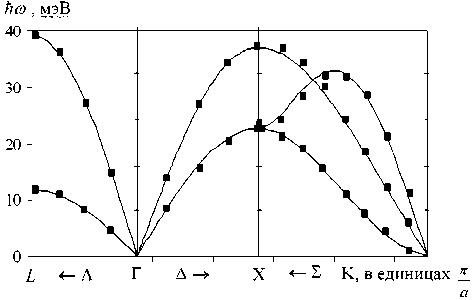
Рис. 4. Кривые дисперсии фононов в Xe при сжатии A V/V q - 0,7

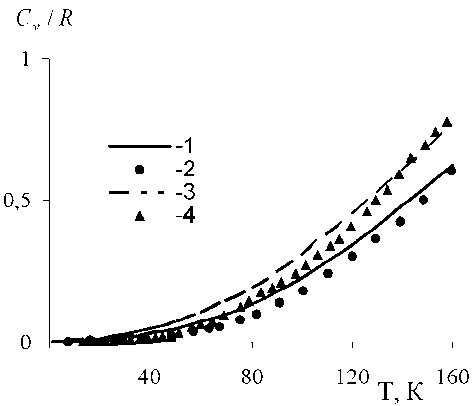
Рис. 5. Температурная зависимость теплоемкости при сжатии A V/V o = 0,7 :

1 – наши расчеты для Ar; 2 – расчет [1] для Ar; 3 – наши расчеты для Ne; 4 – расчет [1] для Ne

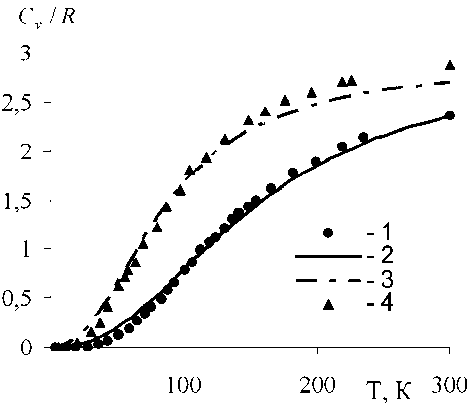
Рис. 6. Температурная зависимость теплоемкости при сжатии A V/V o = 0,7 :

1 – расчет [3] для Kr; 2 – наши расчеты для Kr; 3 – наши расчеты для Xe; 4 –расчет [3] для Xe

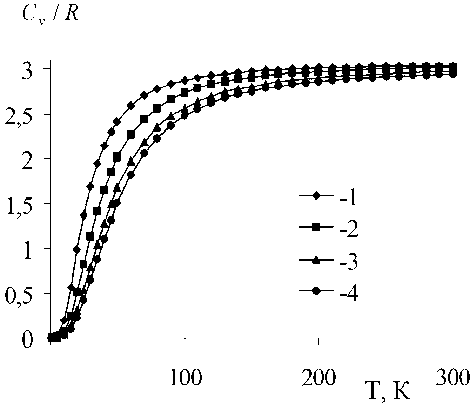
Рис. 8. Кривые дисперсии фононов в Kr при p = 4 ГПа

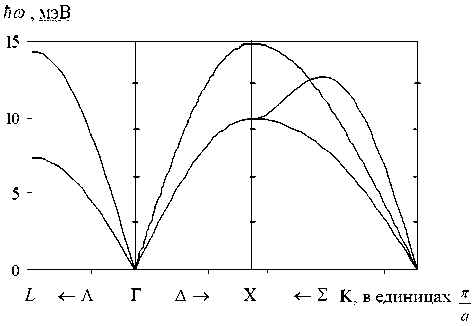
Рис. 7. Температурная зависимость теплоемкости для Kr:

1 - при p = 2 ГПа ; 2 - при p = 4 ГПа ; 3 - при p = 6 ГПа ; 4 - при p = 8 ГПа