Расчет трехмерных композитных балок сложной формы с применением двухсеточных конечных элементов

(рис. 1). Балка представлена шестигранными ДвКЭ v ea (рис. 2), e = 1,...,24 .

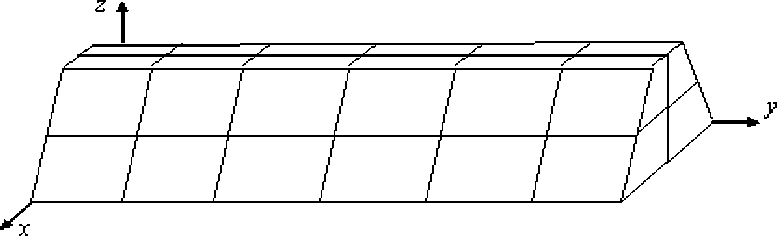
Рис. 1. Балка сложной формы

Основные положения процедуры построения ДвКЭ рассмотрим на примере построения шестигранного ДвКЭ V _e ^a , показанного на рисунке 2.

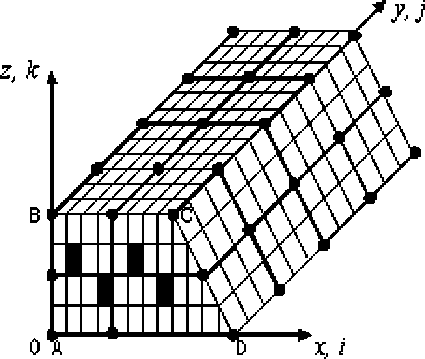
Рис. 2. Шестигранный ДвКЭ V _e ^a

Для построения ДвКЭ V _e ^a используем две вложенные сетки: мелкую и крупную. Мелкая сетка h _e ^a порождена базовым разбиением ДвКЭ V _e ^a , которое учитывает его неоднородную структуру и состоит из конечных элементов 1-го порядка формы куба (шестигранника, треугольной прямой призмы [1, 6]). На мелкой сетке определяем крупную сетку H_e ^a , для узлов которой вводим целочисленную систему координат ijk . Причем оси i , j , k совпадают соответственно с осями Ox ,

Oy , Oz декартовой системы координат Oxyz ДвКЭ V _e ^a . На рисунке 2 показана мелкая сетка базового разбиения ДвКЭ V _e ^a , узлы крупной сетки H_e ^a отмечены точками, сечения волокон закрашены, общее число узлов крупной сетки н е равно 40, i = 1,...,5 , j = 1,...,5 , k = 1,...3 . Отметим, что узлы крупной сетки H_e ^a в плоскостях, параллельных плоскости Oxz , образуют четырехугольный конечный элемент (КЭ) ABCD второго порядка (рис. 2), который имеет 8 узлов. На рисунке 2 узлы отмечены точками. Интерполяционный полином P_a ( x , z ) для КЭ ABCD имеет вид 2.         2.         2.          2

P_a ( x , z) = a i + a 2 x + a 3 z + a 4 xz + a 5 x + a 6 z + a 7 x z + a 8 xz , где a i - постоянные, i = 1,...8 .

При построении базисных функций ф р ( x , y , z ) ДвКЭ V ^ используем полиномы Лагранжа L p ( y ) и базовые функции N p ( x , z ) , которые построены по алгоритмам МКЭ для двумерного интерполяционного полинома P_a ( x , z ) . Общее число базисных функций ф р равно 40 (т. е. в = 1,...,40 ).

Базисную функцию ф р для узла в (крупной сетки н е ДвКЭ У a ) представляем в следующем виде:

ф р ^{( x} , У , ^z ) = N р ^{( x} , ^z ) L p ⁽ У ) ,                                      ⁽¹⁾

где р = 1,...,40 .

Отметим, что вместо полиномов Лагранжа L p ( у ) можно использовать базисные функции N ⁿ n ( у ) , отвечающие интерполяционному полиному P_n ( у ) n -го порядка. Для ДвКЭ У a имеем n = 4 , т.е. полином P ₄( у ) имеет вид

^P 4⁽ У ) = ^b 1 ⁺ b 2 У + b 3 У ^{2 +} b 4 У ^{3 + b}5 У ⁴ , где b i - постоянные, i = 1,...,5 .

Функции перемещений u_a , v_a , w_a ДвКЭ V _e ^a (построенные на крупной сетке H_e ^a ) представим в виде

40                4040

ua = 2ФР uP - va = 2 ФР vp - wa = 2 Фр wp -

Р=1              р=1

где ф р , и р , у р , w p - базисная функция и значения функций перемещений u_a , v_a , w_a р -го узла крупной сетки н е , р = 1,...,40 .

Пусть q a = { u 1 ,..., и ₄₀, v 1 ,..., v ₄₀, w 1 ,..., w ₄₀} T есть вектор узловых перемещений крупной сетки H_e ^a , т.е. q _e ^a – вектор узловых перемещений ДвКЭ V _e ^a . На базовом разбиении ДвКЭ V _e ^a строим функционал П e полной потенциальной энергии. Причем П £ = П e ( q h ) , где q h вектор узловых перемещений базового разбиения ДвКЭ V _e ^a . С помощью (2) вектор узловых перемещений q _e ^h (т. е. вектор узловых перемещений мелкой сетки h _e ^a ) выражаем через вектор q _e ^a узловых перемещений ДвКЭ У a . В результате имеем П e = П e ( q ^a a ) . Из условия д n e ( q ^a _e )/ d q a = 0 получаем формулы для вычисления матрицы жесткости и вектора узловых сил ДвКЭ V _e ^a .

Достоинства ДвКЭ в композитных балках состоят в следующем:

• -    описывают трехмерное напряженное состояние;

• -    учитывают неоднородную (микронеоднородную) структуру;

• -    учитывают сложную форму и сложный характер крепления балок;

• -    порождают дискретные модели малой размерности.

Реализация МКЭ для двухсеточных дискретных моделей трехмерных композитных балок требует меньше объема памяти ЭВМ и временных затрат, чем для базовых дискретных моделей.

Приведен пример расчета по МКЭ балки волокнистой структуры, имеющей поперечное сечение сложной формы. Анализ расчетов балки показывает высокую эффективность применения предлагаемых ДвКЭ.

• 1.    Процедура построения двухсеточных конечных элементов сложной формы. Основные положения процедуры покажем на примере построения композитного ДвКЭ v e сложной формы, который расположен в декартовой системе координат Oxyz (рис. 3). ДвКЭ v e есть прямоугольный параллелепипед размерами 18 h х 24 h х 18 h , имеющий отверстие сложной формы. Считаем, что между компонентами неоднородной структуры ДвКЭ v e связи идеальны, а функции перемещений, напряжений и деформаций этих компонентов удовлетворяют закону Гука и соотношениям Коши, отвечающим трехмерной задаче теории упругости [5], т.е. во всей области ДвКЭ V _e ^b реализуется трехмерное напряженное состояние. ДвКЭ V ^ армирован непрерывными волокнами, параллельнными оси Oy . Область ДвКЭ V ^ представляем базовым разбиением, состоящим из однородных односеточных КЭ V h 1-го порядка формы куба со стороной h [1], j = 1,..., M ; где M - общее число КЭ V h . На рисунке 3 показано базовое разбиение ДвКЭ v e на КЭ V h в плоскости Oxz , сечения волокон (размерами h х h ) закрашены. Базовое разбиение ДвКЭ V ^ учитывает его неоднородную структуру и порождает мелкую узловую сетку V i^h . На мелкой сетке V ih определяем крупную сетку Н % . На рисунке 3 узлы сетки Н^, отмечены точками. Общее число узлов крупной сетки H b равно 60. Крупная сетка V iH вложена в сетку Н ь формы прямоугольного параллелепипеда размерности n 1 х n ₂ х П 3 , которая расположена в целочисленной системе координат i , j , k ; i = 1,..., n 1 , j = 1,..., n ₂ , k = 1,..., n з (рис. 4), n 1 = 4 , n 2 = 5 , n 3 = 4 , узлы сетки H^b _e отмечены точками. Заметим, что не все узлы сетки Н ь являются узлами крупной сетки H eb .

  

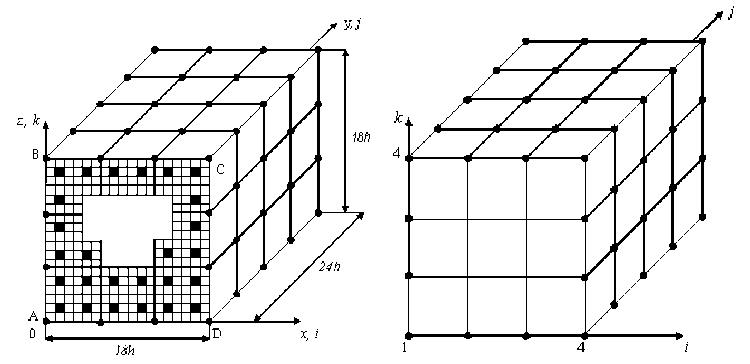
  Рис. 3. ДвКЭ V _e ^b сложной формы

  
  

• 2.          2.          2.            2.            3.              3.            3.            3

Рис. 4. Сетка H_b

При построении базисных функций перемещений / jk ( x, y , z ) ДвКЭ v e используем полиномы Лагранжа L j ( у ) и двумерный интерполяционный полином P b (x, z ) . Общее число базисных функций / jk равно 60. Отметим, что узлы крупной сетки Н % в плоскостях, параллельных плоскости Oxz , образуют прямоугольный КЭ ABCD 3-го порядка (см. рис. 3), который имеет 12 узлов (узлы отмечены точками). Интерполяционный полином P b (x , z ) для КЭ ABCD (см. рис. 3) имеет вид

P b ( x , z) = a j + a 2 x + a 3 z + a 4 xz + a 5 x + a 6 z + a ₇ x z + a g xz + a 9 xz + a io zx + a ji x + a ^2 z , где a i - постоянные, i = 1,...,12 .

Базисную функцию / j ( x , у , z ) для узла i , j , k (крупной сетки H^b _e ДвКЭ v e ) с координатами x _i , y_j , z _k представляем в следующем виде:

/ jk ^{( x} , У , ^z ) = N ik ^{( x} , ^z ) ^L j ⁽ У ) ,                                         ⁽³⁾

где N_ik ( x , z ) - базисные функции перемещений четырехугольного КЭ ABCD (см.рис. 3), построенные по МКЭ и отвечающие полиному P b ( x , z ) , i = 1,...,4 , j = 1,...,5 , k = 1,...,4 ; L j ( у ) - полиномы Лагранжа, которые имеют вид

L j ( у ) =    П     '   ^У" .                                     (4)

а= 1, а*jyj ~ У а

Узлу i , j , k крупной сетки н е ДвКЭ v e определим число в и введем обозначение

N p = / ijk , в = 1,...,60 . Тогда функции перемещений u b , v b , W b ДвКЭ v e (построенные на крупной сетке H _e ^b ) представим в виде

60                   60

ub =2/0 up - vb = 2/P vp - wb =2 Фв WP,

P=1                p=1

где /p, up, vp, wp - базисная функция и значения функций перемещений ub, vb, Wb в-го узла крупной сетки Heb, в = 1,...,60.

Пусть q b = { u 1 ,..., u 60 , v 1 ,..., v 60 , w i ,..., w 60И есть вектор узловых перемещений крупной сетки H _e ^b , т.е. вектор узловых перемещений ДвКЭ V _e ^b . Полную потенциальную энергию П _e ^b базового разбиения ДвКЭ V _e ^b представим в форме [1, 6]

M

П е = 2 (5 q T K h ] q j - q TT P j ) >                                (6)

j = 1²

где [ K j ] - матрица жесткости; P j , q j - векторы узловых сил и перемещений КЭ V j базового разбиения ДвКЭ; T - транспонирование.

Используя (5), вектор q j узловых перемещений КЭ Vjh выражаем через вектор qib узловых перемещений ДвКЭ Veb . В результате получим равенство qj = [ Ab] qb -                                                 (7)

где [ A j ] - прямоугольная матрица, j = 1,..., M .

Подставляя (7) в выражение (6), из условия д П b / d q | = 0 получаем уравнение [ K b ] q b = F e , где

MM

[ K^b_e ] = £ [ A b ] T [ Kj][A b ] , F b = £ [ A b ] T P j ,                      (8)

j = 1                              j = 1

здесь [ K eb ] , F eb - матрица жесткости и вектор узловых сил ДвКЭ V ^ .

Отметим, что процедура построения ДвКЭ неоднородной структуры формы прямой треугольной призмы аналогична процедуре п. 1. На рисунке 5 показаны мелкая и крупная сетки ДвКЭ формы прямой треугольной призмы, узлы крупной сетки отмечены точками, сечение волокна, параллельного оси Oy , закрашено.

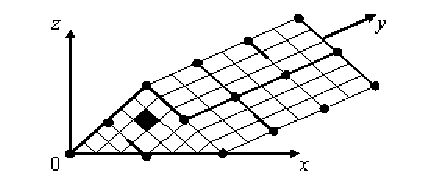
Рис. 5. ДвКЭ формы треугольной призмы

Узлы крупной сетки в плоскости Oxz образуют треугольный КЭ 2-го порядка (6 узлов), для аппроксимации перемещений которого  используем интерполяционный полином вида

• 2       2

• 2.    Результаты расчетов. В качестве модельной задачи рассмотрим расчет композитной консольной балки V волокнистой структуры (рис. 6). Балка V расположена в декартовой системе координат Oxyz , при y = 0 имеем u = v = w = 0 , т.е. балка жестко закреплена. Волокна парал-

• лельны оси Oy . Базовое разбиение R балки V состоит из однородных КЭ Vjh 1-го порядка формы куба со стороной h .

P ( x , z ) = a i + a 2 x + a 3 z + a 4 xz + a 5 x + a 6 z [6], где a i = const .

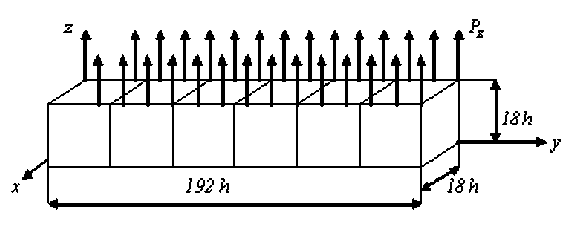
Рис. 6. Балка V ,

Разбиение R учитывает неоднородную структуру балки и порождает мелкую сетку h размерности 19 х193 х19. Двухсеточная модель балки Vo состоит из ДвКЭ У^ с размерами 18h х 24h х 18h (см. рис. 3), построенные по процедуре п. 1, e = 1,...,N, N - общее число ДвКЭ У^ , для балки Уо N = 6. На рисунке 6 показано разбиение балки Уо на ДвКЭ У^ . В узлах мелкой сетки ha базового разбиения балки Уо с координатами xi, yj, z = 18h, где xi = 6h(a -1), a = 1,...3 , yj = 12h + 6h(p-1), в = 1,...31, на балку Vo действуют вертикальные силы Pz = 0,015 . На рисунке 6 схематично показаны силы Pz. Модуль Юнга связующего материала равен 1, волокна – 10, коэффициент Пуассона для волокна и связующего материала равен 0,3. Длина балки L = 192h, поперечное сечение балки с характерными размерами 18h х18h имеет отверстие сложной формы (см. рис. 3).

Результаты расчетов балки V показывают следующее. Максимальное эквивалентное напряжение a h = 3,659 (перемещение w h = 224,697 ) двухсеточной дискретной модели R_A балки V_o отличается от максимального эквивалентного напряжения а о = 3,940 (перемещения w ₀ = 228,802 ) базовой дискретной модели R ₀ на 7,13 % (на 1,79 %). Размерность базовой модели R балки V равна 178560, ширина ленты системы уравнений (СУ) МКЭ равна 1985. Двухсеточная дискретная модель R балки V имеет 1152 узловых неизвестных (т.е. имеет в 155 раз меньше неизвестных базовой модели R ), ширина ленты СУ МКЭ равна 359 (в 5,5 раза меньше ширины ленты СУ МКЭ модели R ). Реализация МКЭ для двухсеточной модели R требует в 855 раз меньше объема памяти ЭВМ, чем для базовой модели R . Эквивалентные напряжения определяются по 4-й теории прочности.