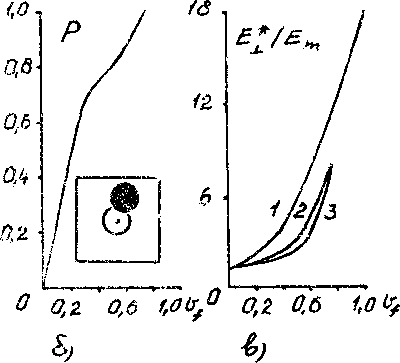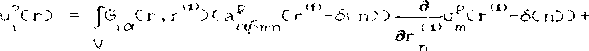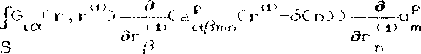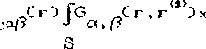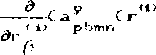Расчет упругих свойств и напряжений на поверхностях разупорядоченных включений композита методом периодических составляющих

Одна из задач микромеханики композитных сред. - учет разупорядоченности во взаимном расположении элементов структуры <: волокон’’ при расчете компонент тензора упругих свойств композита и напряжений в стуктурных элементах. Структуры, в которых разупорядоченность описывается малыми смещениями включений от у периодической схемы укладом. су=< y ,y ,¥ ■> - основные периоды:’, назовем у квазипериодическими. Рассматривая y - кзазипериодическую структуру как деформированную разулорядоченную, поля напряжений на микроуровне не будут периодическими и при простом нагружении композита. Стохастическая же модель у - квазипериодической структуры позволяет решать задачу в у - периодических моментных функциях случайных полей напряжений микроуровня.

.Постановка з ада чи

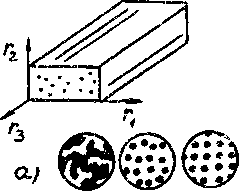
Рассмотрим стохастическую задачу о деформировании области v с границей Г. Рудем считать, что материал области v представляет собой композит матричного типа, причем характерный размер неоднородностей сволокою намного меньше такового области v. Из модельных представлений разупорядоченную структуру композита будем описывать статистически однородными квазипериодическими разрывными по координатам функциями упругих свойств, полагая возможным разбиение структуры композита на однотипные ячейки, в каждой из которых содержится одно независимо разупорядоченное включение рис Л,а. Предположим, что форма и свойства однородных компонентов структуры детерминированы и заданы, на межфазных

Рис.1. а) квазипериодическая структура б) стохастическая ячейка поверхностях идеальная связь структурных элементов. Пусть в некоторой декартовой системе координат определяющие сотношения, связывающие тензор деформаций е^Сг5 и тензор напряжений <^<г:>, задаются в виде

< г D = а С г De С г 3 ,                  С 1 3

I 1              L jm> ।       mn где -^ ^cf.d - случайное поле структурных модулей упругости а ’

f       ,-             ^ГП ГА          К

С 2D

а соСгЭ а С1 -чХ-г)), i jmn             i jmn

«-<„Tir.       - известные тензоры упругости включении и матрицу, u - индикаторная функция включений.

Деформации будем считать малыми, так что выполняются соотношения Коши е Ст D tj

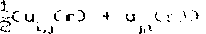
С 3D

Пусть заданы и уравнения равновесия среды a CrD = О.

C4D

4.J

Для определения компонент тензора упругих модулей композитного материала а* _тп , согласно соотношению

w сео

а. .     < е > .

t jmn mn

<... > - оператор осреднения по случайным однородным полям или по объему vd, необходимо решить стохастическую краевую задачу cid-c4d с однородными граничными условиями и = е г ,                          (.53

vr 1J J

r;ie ’* -  - произвольный симметричный тензор второго ранга, имеющий смысл малых упругих макродеформаций.

Ра счет упругих свойств композита

Сп системы дифференциальных уравнений cid.c3d.c4d перейдем к следующей

С a CrDu CrDD = О            C7D ijmn т.п ,j и расчет а*

согласно сез, проводим по зависимостям

а* = <а _Cr3U . СН>,

I jmn       V-^P     -Яртлп u СгЗ = U

e*^ - известный из постановки задачи тензор.

Полагаем известным решение сопутствующей периодической краевой задачи для области v

Сзр CrDup СгЗЗ О. г jmn т.п ,_> ар Crj - а. <.»р<.гЗ + a L 1 - г 3 3 , t ,imn            ijmr»                t ;mn гз = - периодическая индикаторная функция включений.

если разупорядоченность

структуре согласно

отсутствует.

ир = vr

X е г i J j

в кьазипериодической граничные условия и.

методу периодически составляющих /в/, выделим

периодические ооставляющиь д ; лей:

а 0 3 = ар СгЗ + а' СгЗ, и Сг) = ир СгЛ + и’ СгЗ tjmr.             tjrnn             i jmn           »,j            t,j             t ,*

СЮ и от системы дифференциальных уравнений с?з перейдем к системе интегро-дифференциальных:

? ,Сг,г ЭСа* <г и Сг > \ХХ,р}             Ctprnn       m,n

D D dr g сг,га’> - тензор Грина неограниченной однородной среда с тензором упругости t\jmn. \,mn(r>=aljTnr,-htjrnr,-

В с 73 приводится разложение второй производной тензора Грина з. на сингулярную, пропорциональную дельта-функции Дирака scr-r*1*), и регулярную составляющие. "Сингулярное приближение"

решения уравнения типа сю /7/ основано на приближенном раввнстеэ GLja/? своей сингулярной составляющей. Домножим обе части урвнения СЮ на тензор a”. Cr)=atb. CrD- и покрученное уравнение осредним оператором <...>, <а .> =af   .g-t-а1” сi-   , g =<ш> - относительное объемное d Ъ I j      d b i j f d b i j        j          f содержание волокон. Осредненное уравнение решаем в сингулярном приближении и, доказав вспомогательное соотношение р<^

р

constCк?,

ГДе со’ ’ С rD =сс£ г) ~Gf , со’ ’ РС rD =wpC г) -Gf - ПУЛЬСвЦИИ ИНДИКЗТ0рНЫХ функций; к=1.2,...; р - коэффициент периодичности разупорядоченной структуры вычисляется по формуле

-G= р = -----,

CIO?

G C1-G Э f f получим формулу а. .

а р + а С 1 -pD i jmn       v jmn

CH)

- формулу расчета тензора упругих свойств a*jmr> композита с разупорядоченной структурой через a. jmn и ^vjTOn - тензоры упругости композитов с периодической структурой и структурой 11 статистическая   смесь" /э.6,7/, соответственно, и с использованием р - коэффициента периодичности сю). Компоненты *р тензора а : т, вычисляются с использованием численных методов на ячейке периодичности неразупорядоченной структуры /г/, а компоненты тензора ах вычисляются по известным аналитическим г      х jmn формулам /3,6,7/.

Для однонаправленного волокнистого композита с квазипериодической структурой, согласно сП), а*^ % а*37Г,г» чт° и иллюстрирует ресчет е* - модуля Юнга композита в направлениях

I и 2 и его сравнения с е^^р рис.2, если р₍. =гоМПа, у=о,2 и

О 3

модули сдвига и коэффициенты Пуассона ответственно волоком и матрицы композита.

р=О 0<р<1 р = <

Рис.г. Расчет упругих свойств квазипериодического композита а) структурные модели неоднородных сред б) зависимость коэффициента периодичности р от содержания волокон в композите

В) 1 -- е7 /3/, если h = <а >,

2 - Е^ CID, з - Е*р /6/.

Расчет полей напряжений

Поля деформирования на структурном уровне композита вычислим методом периодических составляющих, не прибегая к сингулярному приближению, эффективному лишь при вычислении упругих свойств композита. С использованием соотношений a ,mCrD

uCr) = ирС г-6С nj 5 *и°С г'1 ,

С 1 2D бспс - вектор смещения включения из периодического неразупорядоченного положения в п-ой ячейке, дифференциальные уравнения ст? преобразуем к интегро-дифференциальным:

С130

+ а - (г ?------u С г        -dr

CX/?mn            _ < 1>m              > /3

G^r-r'¹’) - тензор Грина области с границей Гис элементарным неоднородным полем упругих свойств ь <го: однородное поле матрицы са",^ с одним включением са‘ о, координаты центра которого соответствуют координатам центра исследуемого включения б квазипериодической структуре. богласно методу последовательных приближений, решение уравнения cisi представим в виде да асимптотического ряда и'чгг^ у

-6( nDD2i • vdf'¹’

И При t =2,3.. . .

• • г , г tot

  от

  
  

В формуле ci 4) переход от интегрирования по неограниченной области V к интегрированию по в - малой окрестности контура стохастической ячейки, образованного пересечением серединных перпендикуляров к отрезкам, соединяющих центры разупорядочелных включений с рис Л,б), сделан на основе равенства (а^ (r)u^/г)) ,=о и принципа локальности /7/. В s-окрестности i-ой грани стохастической ячейки индикаторная функция взаимного положения включений /° равна 2, если р’..стояние между соответсвующей парой включений в результате разупорядоченности увеличилось, и равна 1/2 - если уменьшилось.

Численный расчет показал, что вблизи межфазных поверхностей включений и°сг) % u^Vr) и поля напряжений здесь с хорошей точностью описываются формулой сЛСг-6'ri))

6С mDD--u v г -6С nD J ? ydr - < t> m дг

Расчет по формуле с 15)

приведем для армированного

t,, .ненаправленными   волокнами

композита,   обладающего при

отсутствии разупорядоченности волокон тетрагональной симметрией структуры и упругих свойств. При Ет=1ГПа и pm=o,35 - модуль Юнга и коэффициент Пуассона матрицы, с ef=0,545 - относительное объемное содержание жестких волокон, расчитаем рис.З радиальных о„/р5 и касательных р сР) напряжений на межфазной поверхности одного из разупорядоченных волокон при нагружении композита в поперечной направлению армирования плоскости, соответствующего ©^=0,30, е*2=-о,1г. Безразмерные координаты с отнесенные к радиусу волокна) центров поперечных сечений волокон при совмещении начала системы с центром поперечного сечения исследуемого сна рисунке центральной» волокна следующие: сг,г;о,г), ссдг.дл; сг,2;о,^.    со;-г,4;>, имеющих в черазупорядоченном состоянии координаты с-г,4;о?,   с о;а.4);

л. со;-г,4). На рис.з штриховой линией показаны расчеты соотве ттвующих величин по методам граничных элемент ов и локального приближения /1.в/.

Рис з. Межфазные напряжения на поверхности разупорядоченных волокон.

Таким образом, решение задачи теории упругости для области с ми- н ими включениями методом периожческих состамнющих с хорошей точностью сводится к последовательному решению двух значительно более простых задач: на ячейке периодичности и на стохастической ячейке. К решению задач на ячейках применяются современные численные методы, например метод граничных элементов.