Расчет вектора Умова-Пойнтинга и силы давления электромагнитной волны на однородный диэлектрический цилиндр

Обычно задачу манипуляции микрочастицами рассматривают для 3D случая, например, для частиц сферической формы. Впервые теоретическую задачу давления света на сферу с помощью теории Ми рассмотрел Дебай в 1909 [1]. В общем случае сила давления света на микрочастицу должна рассматриваться с помощью максвелловского тензора напряжений электромагнитного поля [2]. Впервые сила давления слабосходящегося гауссова пучка на сферическую частицу с помощью теории Ми была оценена в [3], а для “острой” (непараксиальной) фокусировки гауссова пучка в [4,5]. Пользуются популярностью и приближенные методы расчета силы, действующей со стороны света на частицу: метод геометрической оптики с учетом френелевских коэффициентов отражения и преломления [6], который применен для больших

, _ 2п значений параметра q = k 0 a >>  1, где ^k о = 7~~ ^л о

– волновое число света в вакууме, a – радиус сферы, охватывающей объект, и метод градиентной и рассеивающей сил [7], применимый для рэлеевских частиц (q<<1). В [8] рассмотрено еще одно приближение для расчета силы света, действующей на микрочастицу: приближение связанных диполей. В [9] показано, что градиентную и рассеивающую силы можно получить из уравнений Максвелла и тензора напряжений. Полученное в [9] вы- ражение для силы давления света справедливо при условии qn 1 - n2| < 1, где n1 и n2 -показатели преломления среды и частицы. В [10] с помощью тензора напряжений получено выражение для силы света, действующей на сферическую частицу с керровской нелинейностью.

Для численного моделирования удобно перейти от 3D случая к двумерному случаю. Это приведет к существенному сокращению объема и времени вычислений, хотя задачи дифракции на сфере и на круглом цилиндре во многом аналогичны [11]. Поэтому в работе рассматривается дифракция цилиндрической электромагнитной волны ТМ-поляриза-ции на 2D однородном диэлектрическом цилиндре с сечением произвольного вида. Получены выражения для силы давления света на цилиндр. Вектор этой силы лежит в плоскости падения, перпендикулярной оси цилиндра, и выражается через векторы напряженности электрического и магнитного полей электромагнитной волны внутри и вне объекта.

Для расчета 2D поля дифракции ТМ-по-ляризованной волны разработан быстрый итеративный алгоритм, аналогичный алгоритму для ТЕ-поляризованной волны [12]. Алгоритм обладает работоспособностью при условии, что qni - n 21 < ^ . Приводятся результаты численного моделирования дифрак- ции непараксиального цилиндрического гауссова пучка на диэлектрическом круглом цилиндре. Рассчитано поле направлений вектора Умова-Пойнтинга для этой задачи и проекции силы давления света.

Сила давления светана микрообъект

В [1] приведена формула, выражающая сохранения полного импульса системы электромагнитного поля плюс объект V, ограниченный поверхностью S:

9 г .      9           г

J Pidv + p     Jo JLlJs, d t V1            d t          S 1

где P_i – координаты вектора импульса электромагнитного поля ( V ₁ и S ₁ объем, ограничивающая его поверхность, который включает объект V e V 1 ), который связан с векторо м Умова-Пойнтига соотношением:

I dPA.

F u / = -J(Oik)nkdS, так как

» A’ М»AV=0.

dt VV

Можно показать, что:

— = — { Re ( i 8 E ( x ) e ⁸ t ) Re ( H_z ( x ) e* ⁸ t b +

\ dt / 4nc          y"

+ ^Re ( E y ( x ) e i ⁸ t ) Re ( i to H z ( x ) e i ⁸ t -

• - ^Re ( i ro E z ( x ) e i ⁸ t ) Re H y ( x ) e i ⁸ t -

• - ^Re ( E z ( x ) e i ⁸ t ) Re ( i ro H y ( x ) e i ⁸ t ^} = 0 , (7) где Re(…) – реальная часть комплексного

  числа,

  
  

1 ^T

(f ⁽ t )) = ^ J f ⁽ t ) ^dt . Аналогично

T ₀

P = S = — E ^х н ] , c ²    4 п c^L

P _{0 i} – координаты вектора импульса объекта,

9Р

0 i

– координаты вектора силы давления

света на объект;

о, = —

4п

V

E li

H

А

Ь»

- E₍E_t - H . H k

; (3) J

для других проекций вектора импульса электрического поля можно показать / 6РД =1щр\ = ₀

\ d t / \ d t / ’

Для получения выражения для усредненного по времени тензора напряжений (3) учтем, что

R Re ( E i ( x ) e i ⁸ t ) Re ( E_y ( x ) e i ⁸ t | =

о _ik - максвелловский тензор напряжений электромагнитного поля ( о _ik = о _ki ); E , H - векторы напряженностей электрического и магнитных полей в вакууме.

После усреднения по времени за период т 2п

T = — монохроматического света:

= 2^{Re [ E} i ^{( x} ) ^E * ^{( x} ) ] -            (8)

Тогда вместо (5) получим:

F x = ^j{ ₂ ^{[ E} x I^{2 +} H x I² -I ^E y |² -

- H y I² - E - Г - H = r] dS x +

+ Re ( E_xE * + H_xH * "dS_y + Re ( E_xE * + H_xH * ) dS _z} xy   x y y      xz   xz z

E ( x , t ) = Re { E ( x ) e ⁸ t }

H ( x , t ) = Re ^ H ( X ) e i ⁸ t } вместо уравнения (1) получим:

F y = ^J{ 1^[ E l² +1 H l²-! ^E x l² -

- H x |²-I ^E- |²-I H -\² dS , +

+ Re ( E_yE_z * + H_yH * ) dS _z + Re ( E_yE_x + H_yH * ^dSS _x } yz y z z       yx y x x

Fz - 8^ 2 ^{[2 +|}     ^ Ex'^{1 2} —

- H x i^! -I E , |²-I H y I² k+

+ Re ( E z E X + H z H X V ds + Re ( EE + H H dS y }

5z                      dz , , где    dSx =- — dxdy ,    dSy - ' dxdy , dx                dy dSz - dxdy, E 1 = Ex, E2 - Ey, E3 = Ez (для

H _i и F_i аналогично).

Перепишем выражения (9) для силы давления света на микрообъект в 2D случае. Для ТЕ-поляризации ( H_x - E y - E_z - 0) электрическое поле направлено вдоль оси X: E_x * 0, Z – оптическая ось, 2D-объект имеет вид цилиндра с произвольной формой сечения и имеет бесконечную протяженность вдоль оси X. Плоскость YOZ – плоскость падения света. В этом случае соотношение (9) примет вид:

F x - 0 ,

F =—f|1 [ h I2 - Ex |2 - |hz |2 W + y 8яП2 y| x| z| y

S ₁

+ Re ( H y H’ * ds }.

F. = — fl11H|2 -E|2 -HГ]dS.- + z   zxyz

S 1

+ Re ( H z H * dS y } .         (10)

Здесь S1 уже контур, охватывающий сечение объекта в плоскости YOZ. Сила Fz – направлена вдоль оптической оси и является аналогом рассеивающей силы для рэлеевских частиц [7], а Fy – направлена поперек оптической оси и является аналогом градиентной силы [7].

Связь между проекциями H_y , H_z и E_x следует из уравнений Максвелла:

H = - L H - i y k 5z ’ z k dy

2n где k - "г— - волновое число света с длиной А волны А. Аналогично (10) сила давления света с ТМ-поляризацией на 2D объект будет иметь следующие проекции

( E x - H y, - H z - 0):

F x - 0

f =—f|Де I2-\e I2-\h Ms + y 8л?12l y|        z|         x| y

S ₁

+ Re ( E , E‘ z ) dS, } ,

F z - f { 1 ^[ E z^ -I E y' I² "I H x l²- dS '

S 1

+ Re ( E.E’y 'dS, } ,           (12)

где (как и в уравнении (10))

dS_y - n_ydl - sin ф dl - dz

и dSz - nzdl - cos фdl - dy , dl – элемент дуги.

Расчет поля дифракции

2D электромагнитной волны

В [12] описан быстрый итеративный алгоритм расчета поля дифракции двухмерной электромагнитной волны с ТЕ-поляризацией на диэлектрическом микрообъекте. Рассмотрим далее аналогичный алгоритм для случая ТМ-поляризации. Будем исходить из нагруженного интегрального уравнения Фредгольма второго рода, описывающего двумерную задачу дифракции [13] ( ф - H_z ).

Ф ( y , ^z ) ^{- ф}0 ⁽ y , ^z ) s ^- ik 0 (4 1) •

• ff ^{ф (} ^ , n ) H 0^{2) (} k V ⁽ y ^-9 ^{2 + ( z -}n ^{) 2} ) d ^ ^d П ⁺

V

⁺ i ( ^ 4T^) f ^{ф (} ^ n ) d n ^H 0^{2) ( k} V( y -I )^r + ( z -ⁿ ) ^? )^ ¹

(13) внутри объекта площадью V, ограниченного контуром S, т.е. ( y , z ) е V и

\ Г A i^k 0^(£- 1)

^{ф (} y , ^z ) ^-ф0 ⁽ y , ^z )-----

• JJ ф ( ^ , n ) H 02) ^{( k} 7⁽ У -9 2 + ^{( z -}n ^{) 2} d ^ d п + V

• 3 ^-1 [ з ( ф n ( ^ , n ) P ( ^ , п ) ) • з ( н 0²⁾ ( k 7 ^ ² +п ² )) ] -

+ ^ (^—1) f ^{ф (} ^П ) т^ H 02) ( ^k 7⁽ У -9 2 + ^{( z} -n ^{) 2} V¹ 4 s 5        о n

-Y i^{k 0(}4 1) ^з-^[з(ф n ⁽ ^ n ) G ⁽ ^ , п ) П у ) .

снаружи объекта при ( у , z ) ^ V , где £ - диэлектрическая проницаемость внутри объекта, H ₀ ⁽²⁾ ( x ) – функции Ханкеля нулевого порядка,

^

7 ^2+п2

H (⁽²⁾ ( k 71 27 7 2 )

)

^“

^- Y i^k 0 ⁽4 1) ^з-^[з(ф n ( ^ n ) G ⁽ ^ , n ) n z ) .

ф ₀ - амплитуда падающей световой волны, n – внешняя нормаль к поверхности объекта.

Интеграл по контуру в (13) и (14) можно представить через преобразование Фурье, введя функцию контура объекта.

Г

•з

_ п JV +п

_? H ™ ( k 71 27^2 ) ;

^{+ (1 -}Y ^{) ф} n ⁽ у , ^z )

G(У, z ) =

1, ( у , z ) е 5 0, ( у , z ) е 5 ^.

внутри объекта ( у , z ) е V и

Тогда f фn(У,z)dnH02)k(у-У2 +(z-n)2 'dll =

^ф n +1 ⁽ у , ^z ) = Y ^фо ⁽ у , ^z ) ^- Y ik 0 (7 1)

• з

= k ^{з 1 [з(ф (} у , z ) G ⁽ у , ^z ) П у ) •

• з-1 з(ф n (^, n) p (^, n-)• з(н 02) (k 7 ^2 +п2)) -

^- Y ik ⁰4 £ 1) ^{з-1 [з(ф} n ( ^n ) G ( ^п ) ^п у ) •

^

J^2 +n

)

=H 1⁽²⁾ ( k 7 2 +n ² ) )

+

^

7 ^2+п2

•з

^{+ з(ф (} у , z ) G ⁽ у , z ) n z ) •

H 1(2) (k 77 +п2) J

^“

H f²) k    .  7

где n = ( п_у , n_z ) - единичный вектор внешней нормали к контуру S, ( у , z ) е 5 , 3 и з ^-1 -прямое и обратное 2D Фурье-преобразования. Аналогично, интеграл типа свертки по площади объекта V в (13) и (14) можно переписать через преобразование Фурье с помощью функции объекта

,    . [1,fe,п ) е V

P ^ пМ / а._т/.       (17)

[ 0, ( ^ , п ) £ V            ^{v 7}

Итеративный алгоритм решения интегрального уравнения (13) будет иметь вид:

А А A     ik 0(£- 1)

^ф n +1 ⁽ у , z ) = у^ф о ⁽ у , z ^{) £ -} y —4—

•

- y ik 0 ( ^£ 1) ^з-1^[з(ф n ( ^n ) G ( ^n ) n z ) • 4 s

"^з^ 4ё-+П

)

H 1⁽²⁾ ( k 7 ^ ² + п ²) /

^{+ (1 -} Y ^)ф _п ⁽ у , ^z )

снаружи объекта ( у , z ) ^ V , где ф _{n + 1} и ф _n -

рассчитанные комплексные амплитуды поля на (п+1)-й и (п)-й итерациях, Y - параметр релаксации.

Численное моделирование

Для проверки работоспособности алгоритма проводилось численное сравнение полей дифракции плоской ТМ-поляризованной волны на круглом диэлектрическом цилиндре, рассчитанных с помощью полученного алгоритма и с помощью известных аналитических формул.

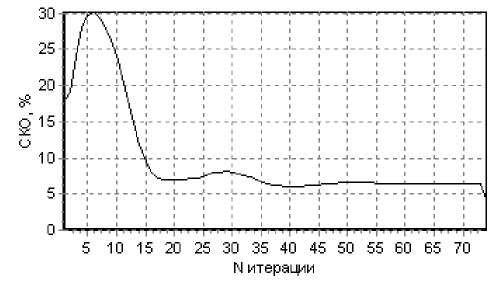
а)

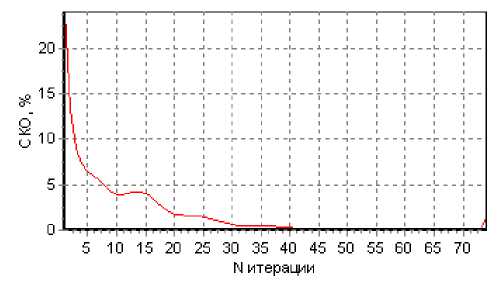
б)

Рис. 1. а – среднеквадратичное отклонение модуля амплитуды магнитного поля, рассчитанного данным алгоритмом, от точного решения в зависимости от числа итераций; б – среднеквадратичное отклонение двух модулей амплитуд магнитного поля, рассчитанных данным алгоритмом, для двух соседних итераций, в зависимости от номера итерации

Если сравнить данные графики (рис. 1) с аналогичными, полученными для ТЕ поляризации [12], можно заметить, что устойчивость алгоритма для ТМ поляризации выше, чем для ТЕ, но точность ниже. Это обусловлено ошибкой расчета интеграла по контуру объекта на границе раздела двух сред.

Параметр релаксации γ был подобран экспериментально для случая дифракции на круглом цилиндре. Подбор был осуществлен на поле 256x256 отсчетов, 2,5x2,5 мкм. Диаметр цилиндра был равен длине волны в d = λ =1 мкм, диэлектрическая постоянная цилиндра, находящегося в вакууме, ε =2. При этих параметрах среднеквадратичное отклонение рассчитанного за 13 итераций модуля амплитуды напряженности магнитного поля от точного решения в зависимости от параметра γ показано на рис. 2.

Как видно из рис. 2, достаточно широкий диапазон параметра γ приводит к устойчивой работе алгоритма, наилучшим являет-

25 16 14 12 10	0		3         0.	35       0	4          0.	45       0	5         0.	55      /

Рис. 2. Зависимость невязки на 13-ой итерации от коэффициента γ ся γ =0,35..0,4. Экспериментально было найдено, что алгоритм не расходится при усло-π        2π вии, что q n1 - n2 < , где q = a , a - ра-2λ диус окружности, в которой вписано сечение цилиндрического объекта, n2 и n1 - показатели преломления объекта и среды.

На рис. 3 приведены примеры расчета картин дифракции на круглом цилиндрическом диэлектрическом объекте непараксиального гауссова пучка с ТЕ- и ТМ-поляризован-ной волной. Параметры расчета: все поле 10x10 мкм, 512x512 отсчетов, длина волны λ =1 мкм, диаметр цилиндра D=1 мкм, диэлектрическая проницаемость объекта ε =2, диэлектрическая проницаемость среды ε ₀=1, радиус перетяжки пучка в фокусе σ =0,5 мкм. На рис. 3а,б объект расположен точно в фокусе, на рис. 3в,г смещен вверх (по оси Y) на половину длины волны. Время расчета поля с ТЕ поляризацией на компьютере PIII Celeron 1000 MHz составляет 31 секунду, всего 155 итераций. Время расчета поля с ТМ поляризацией составило 1 минуту и 3 секунды, было сделано 72 итерации. Критерий остановки итераций в обоих случаях одинаковый: невязка между шагами должна быть меньше 0,0001.

Вектор Умова-Пойнтинга

S = ¹ Re 4 π c

[ E × H ^* ]

в)

г)

в)

г)

Рис. 3. Модуль напряженности магнитного поля (а,в) ТМ-волны и электрического поля (б,г) ТЕ волны, которые описывают дифракцию непараксиального гауссова пучка на круглом диэлектрическом цилиндре: цилиндр в фокусе пучка (а,б) и смещен вверх на пол длины волны (в,г)

Рис. 4. Поле направлений вектора Умова-Пойнтинга для дифракции электромагнитной ТЕ-поляризованной (а,в) и ТМ-поляризованной (б,г) волны на круглом диэлектрическом цилиндре: освещающая волна плоская (а,б), гауссовая (в,г) (цилиндр в перетяжке гауссова пучка)

для 2D задачи имеет вид:

для ТЕ-поляризации:

E Z 0 ( ^z , У ) =

S = — 4 n ck

( dE * ]        (    dE *

e y Im ^Ex”T 1 + e z Im l E x j

I     dy )        V     dz

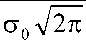
, (20)

”

г

I exp<

где e_y и e - единичные векторы вдоль ос е й

-го

2 о 0

+ ik

⁽ z ^ + У^ ¹ -^ ² )’ d ^ , (22)

Y и Z, Im(…) – мнимая часть числа, c – ско-

где о 0 - параметр гауссова пучка, связанный

рость света в вакууме; для ТМ-поляризации:

S = —

4 n c

e Im H yx

v

*

dH dy )

+ e z Im H x

v

dH * ) dz ₎

, (21)

На рис. 4 показаны поля направлений вектора Умова-Поинтинга (20) и (21), наложенные на картины дифракции плоской (рис. 4 а,б) волны, и гауссова пучка (рис. 4 в,г) с длиной волны X =1 мкм, диаметр цилиндра D=1 мкм, диэлектрическая проницаемость объекта е =2, диэлектрическая проницаемость среды е 0 =1, радиус перетяжки пучка в фокусе о =0,5 мкм.

Амплитуда падающего непараксиального пучка рассчитывалась по формуле [14]:

с радиусом его перетяжки ш соотношением: 1

о ₀ = —. к ш

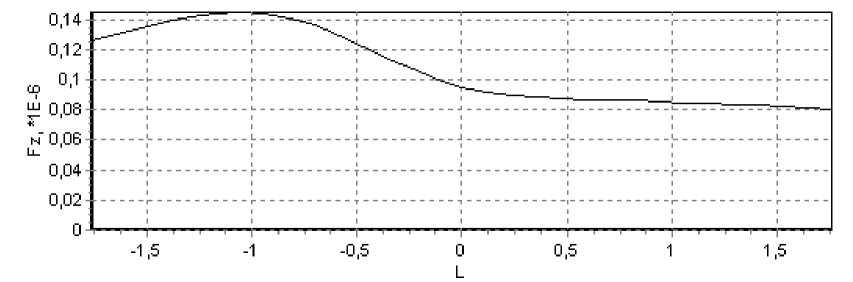
Силы, расчитанные по формуле (10), действующие на круглый цилиндр в случае ТЕ-поляризованной волны, представлены на рис. 5. Параметры эксперимента: все поле 10x10 мкм, 512x512 отсчетов, длина волны X = 1 мкм, диаметр цилиндра D=1 мкм, диэлектрическая проницаемость объекта е =2, диэлектрическая проницаемость среды е 0 =1, радиус перетяжки пучка в фокусе о =0,5 мкм. Смещение от центра L имеет размерность мкм. Силы даны в безразмерных единицах.

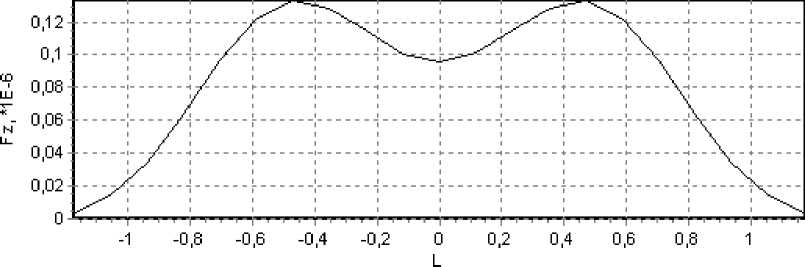
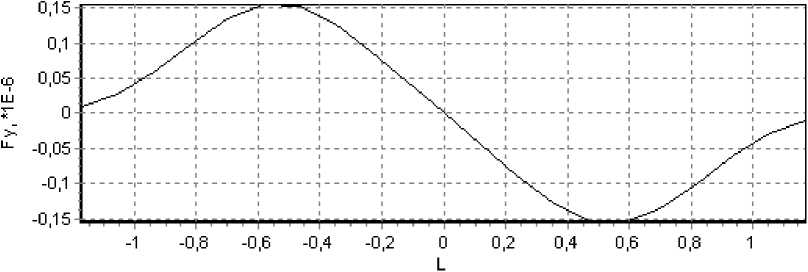
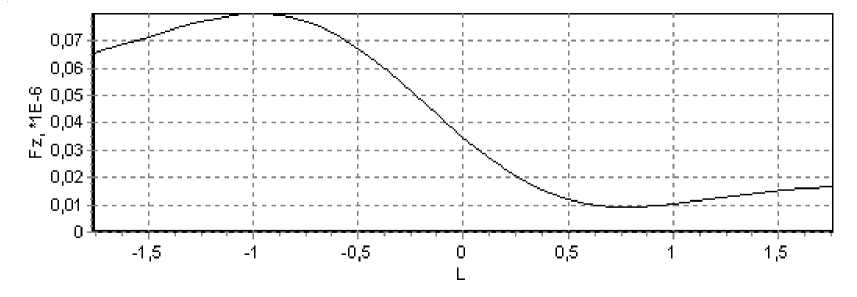
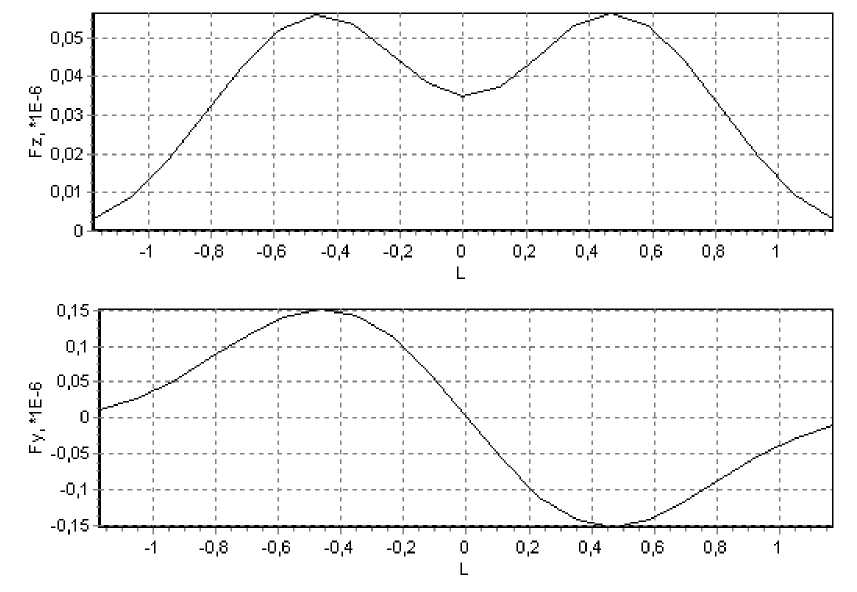
Аналогичные силы в случае ТМ-поляри-зации, рассчитанные по формуле (12), представлены на рис. 6.

а)

б)

Рис. 5. ТЕ-поляризация:

а – зависимость силы Fz от смещения L объекта вдоль оси Z через центр перетяжки (Y=0); б – зависимость сил Fz и FУ от смещения L объекта вдоль оси Y через центр перетяжки (Z=0)

Заключение

В работе получены следующие результаты: разработан итеративный алгоритм для быстрого расчета поля дифракции ТМ-по-ляризованной электромагнитной волны на цилиндрических диэлектрических микрообъектах;

с помощью быстрого преобразования Фурье за 74 итераций, которые на компьютере Celeron 1000 MHz выполняются за 1 минуту 18 секунд, было рассчитано поле дифракции плоской волны на круглом цилиндре, отличающееся от точного решения в среднем на 4%;

– численно показано, что параметр релаксации γ итеративного алгоритма можно варьировать в широком диапазоне 0,3< γ <0,525 для достижения практически одинаковой точности решения задачи дифракции;

– рассчитано поле дифракции непараксиального гауссова пучка на диэлектрическом круглом цилиндре, диаметр которого сравним с диаметром перетяжки и расположен вблизи этой перетяжки;

• – рассчитан вектор Умова-Пойнтинга для дифракционной картины ТМ- и ТЕ-поля-ризованной волны на диэлектрическом

  

  а)

  
  
  

  б)

  Рис. 6. ТМ-поляризация:

  а – зависимость силы F_z от смещения L объекта вдоль оси Z через центр перетяжки (Y=0); б – зависимость сил F_z и F_y от смещения L объекта вдоль оси Y через центр перетяжки (Z=0)

  
  

микрообъекте;

• - рассчитаны силы, действующие на круглый цилиндр в области перетяжки непараксиального гауссова пучка в случае ТЕ- и ТМ-по-ляризованной электромагнитной волны.

Работа выполнена в рамках российско-американской программы “Фундаментальные исследования и высшее образование” (грант CRDF REC-SA-014-02), поддержана грантом НШ-1007.2003.1, грантом Министерства образования и Правительства Самарской области.