Расчет векторных мод оптического волновода
Автор: Котляр В.в, Шуюпова Я.О.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Методы и элементы компьютерной оптики
Статья в выпуске: 27, 2005 года.
Бесплатный доступ
В работе рассмотрен метод расчета собственных электромагнитных мод волноводов, основанный на методе согласованных синусоидальных мод. Соответствующее программное обеспечение, разработанное в среде MathLab, применено для расчета мод слабонаправляющего волокна со ступенчатым профилем показателя преломления.
Короткий адрес: https://sciup.org/14058658
IDR: 14058658
Текст научной статьи Расчет векторных мод оптического волновода
Существует множество различных методов расчета собственных мод волноводов, но далеко не все из них могут обеспечить полностью векторный анализ [1-6], многие ограничиваются лишь приближенными результатами в рамках скалярной теории. Тем не менее, в литературе не однократно подчеркивалась необходимость именно векторного подхода к исследованию, например, таких сложных, но перспективных структур как фотонные волноводы.
Задачей настоящего исследования были реализация и апробирование векторного подхода метода согласованных синусоидальных мод, основанного на представлении каждой из компонент электромагнитного поля моды в виде суперпозиции гармонических функций, представляющих собой локальные моды однородных областей сечения.
Достоинство выбранного метода по сравнению с методами, основанными на конечно-разностном подходе [5, 6], состоит в том, что он позволяет получать в качестве результата непрерывные функции, также, как и метод [4], использующий функции Грина. Но подход, рассмотренный в работе [4] в силу своих особенностей может быть применен лишь к круглым волокнам, тогда как метод согласованных синусоидальных мод [1-3] - к волноводам с произвольным сечением.
Данная работа является логическим продолжением работы [1], в которой рассматривался скалярный случай. Также как в [1] здесь справедливы предположения о возможности разбиения сечения волновода на конечное число строк и столбцов, таким образом, что ни одна ячейка этого разбиения не содержала бы неоднородностей. На границах сечения предполагается наличие так называемых электрических или магнитных «стенок», определяющих граничные условия задачи. Основываясь на этих допущениях, строится алгоритм численного расчета констант распространения мод и построения функций их электрических и магнитных компонент.
Отличия векторного описания мод оптического волновода от скалярного
Принципиальное отличие векторного случая от скалярного в рамках метода согласованных синусоидальных мод состоит в том, что необходимо рассматривать локальные моды двух различных поляризаций – ТЕ и ТМ, поскольку обе они вносят свой вклад в формирование гибридной моды волновода, выражение для которой принимает вид:
№
( m ) ( m ) ( m ) ( m ) ( m )
F ( x, y ) = ^ ^ [ u pk ( x ) F spk ( y ) + u pk ( x)F apk ( y )], (1)
p = e, h k = 1
где F представляет собой любую из электрических или магнитных компонент поля моды, а внешняя сумма соответствует суммированию по поляризациям: ТЕ- p = h , ТМ- p = e . Обычно, ТМ-поляризация характеризуется отсутствием продольной составляющей электрического поля E z = 0, а ТЕ-поляризация – отсутствуем магнитной составляющей B z = 0 . В отечественной литературе - наоборот. Рассмотрим подробнее локальные моды, входящие в выражение (1). Локальная x - мода, имеет вид:
и (т ) ( x ) =
Г k,
к ( m )
V kpk 7
u £ l )cos[ k^A x - x ( m ) )] +
U sin[k^k( x - x(m))], kxpk
здесь учитывается поляризация, и, в отличие от ска-
лярного случая, введен множитель
k о
К ( m )
I kpk 7
необ-
ходимость которого будет объяснена далее. Величины Fs ( p m ) и Fa ( p m ) , входящие в выражение (1), оп-
ределяются через параметры волновода и локальные У - моды, как показано в таблице 1.
Таким образом, выражение (1) принимает вполне определенную форму для каждой из компонент векторов E ( x , y ) и cB ( x , y ) :
( m ) № ( m )
Ex ( x , У ) =^ uhk k = 1
kz ( m ) № ( m )
( x ) ^ k ( У ) - ^ !i ek ( x )
( m ) №
Ey ( x , У ) = - ^
k = 1
k 0
k = 1
( m )
V k ( У )
2 ( m )
k o s ( У )
,(3а)
ue m )( x )
( m ) kek
V k.
№
E z m ) ( x , y ) =- ^ u hm ) ( x )
k = 1
i ф km ) ( У )
o 7
№
( m )
V k ( у )
( m ) ,
7 7 y )
+ z.>-em •( x )
k = 1
ik , j^ km l k 2 .(m ) ( y ),
m )(x VM( m )f ф )( У ) + У »< m ) , m m )
cBx (x,y) = / uhk (x) 2 + 2—iuek (x) 1 Vk v ), k=1 kо k=1 ko
(3б)
(3в)
(3г)
cB^ ym ) ( x , y )
= E u hm ( x )
к = 1
( к ( m ) Y l к о J
Ф к m ) ( y ),
(3д)
cB
)
(
x
,
y)
=-
E
u
hmm\
x
)
'
Ф
m)
(y)
-
EE
U
Таблица 1. Симметричные и антисимметричные y -компоненты поля, выраженные через локальные моды
|
ТЕ |
ТМ |
|||||
|
F |
T? ( m ) F sh |
T- ( m ) Fah |
Б ( m ) se |
Б ( m ) ae |
||
|
E x |
( J ф ( m ) ( y ) l к 0 ) |
0 |
0 |
- j y j m )( y L к 02 £( m ) ( y ) |
||
|
E y |
0 |
0 |
- |
к ( m )' kek |
2 y ( m ) ( y ) J £ ( m ) ( y ) |
|
|
i к 0 |
||||||
|
E z |
0 |
- / Ф ( m ) ( y ) к 0 |
ikz l к 02 J |
y > ( m ) ( y ) £ ( m ) ( y ) |
0 |
|
|
cB x |
0 |
« ^ ( y ) к 02 |
[ к^ J y ( m ) ( y ) l к 0 7 |
0 |
||
|
cB y |
к к ( m )Y к ^к- Ф ( m ) ( y ) к п l 0 7 |
0 |
0 |
0 |
||
Это гибридные моды, из которых нетрудно получить по отдельности ТЕ- и ТМ-моды.
В таблице 1 и выражениях (3) ф ( y ) - рассмотренные подробно в скалярном случае [1] локальные y - моды, в данном контексте соответствующие ТЕ-поляризации, что означает абсолютную идентичность выкладок для этих мод с выкладками, проведенными для скалярного случая. Моды y ( y ), представляющие ТМ-поляризацию, имеют следующий вид в столбце m разбиения:
Здесь P ( i ) и Q ( i ) также, как в скалярном случае матрицы вида:
( n,l )
y (y ) = y n,l W ( n) (y - y ( n ) )] + sin k yn ) ( y - y ( n ) )]. (4) k y )
Здесь величины y" ’ l ) и y an ’ 1 ) - неизвестные, подлежащие определению значения функции и производной локальной y - моды соответственно на границах разделения однородных областей (ячеек). Для них справедливы соотношения:
|
P ( i ) = |
" cos[ к yi ) d (0 ] sin[ к yi ) d ( i ) ]/ к y ) " _- sin[ k Уi ) d ( i ) ] k Уi ) cos[ к y ) d (0 ] _ |
, (9) |
|
Q ( i ) = |
cos[ к^^ d ( i )] - sin[ к () d ( i )]/ к y ) " |
(10) |
|
L sin[ ку^ 1 ку c°s[ ку^ 1 J |
||
|
Г 1 0 1 |
||
|
W ( i +1) = |
n £ ( 1 + 1) , i = 1 ,N - 1. |
(11) |
|
L 0 £ ( i ) J |
||
|
Г 1 |
0 1 |
|
|
JZ( i ) = V |
£ ( 1 ) , i = 1 ,N - 1. |
(12) |
|
£ ( i + 1) |
||
y Sn , r ) = y Sn + 1- 1 ) , y an ' r ) = y an + 1, 1 ) £ n ) e ( n + i)
Для мод y ( y ) матричные равенства, вытекающие из требования их непрерывности (5) и условия (6), налагаемого на их производные, имеют форму:
y Sn ’ r ) y a n’ r )
= P ( n ') W ( n ') P ( n '-1) W ( n '-1) _ W (2) P 1
y^11 y a1 )
, (7)
y S 1 )
y an + 1,1 )
= Q n '+ 1) V< n '+ 1) Q n '+ 2) ^ n '+ 2) ^ V N - 1) Q N
y SN , r )
y aN , r )
. (8)
Очевидно, что матрицы W ( 1 + 1) и V ( 1 ) являются взаимно обратными и зависят исключительно от диэлектрической структуры сечения волновода. Соотношения (7) и (8) также, как их аналоги для ТЕ-поляризации, используются для расчета величин, входящих в характеристическое уравнение относительно к к :
s (n) v (nV) v (n' + 1 ’° -s (n' + 1 ) v an'r) v (n' +1 n = о. (13)
Не вызывает сомнений факт, что корни характеристических уравнений для различных поляризаций различны, поэтому необходимо ввести соответствующие обозначения, во избежание путаницы. Пусть ккк - набор решений уравнения соответствующий ТЕ-случаю, а кд - решения уравнения (13), описывающие локальные ТМ-моды.
Также незначительные изменения для локальных ТМ мод необходимо внести в формулу для расчета интеграла нормировки:
1 у ( N +D
/" 1 11 - у <" , 1
) dy = 1. e ( У )
Таким образом, при расчете векторных полей задача усложняется ровно вдвое. Теперь алгоритм отыскания локальных у - мод представляется следующим:
- для каждого столбца сечения необходимо найти
K корней khk характеристического уравнения, оп ределяющих моды ф(у) при определенных граничных условиях (электрические или магнитные стенки),
- затем рассчитать константы ф ^n ’ l ) , ф кn ’ l ) , фкn ’ r ) , ф аn ’ r ) , исходя из условия нормировки, чтобы окончательно сформировать K у - мод, соответствующих случаю ТЕ-поляризации;
- для каждого столбца сечения необходимо найти ровно столько же K корней kpk уравнения (13), определяющих моды v(у) с граничными условиями противоположными ТЕ-случаю. То есть, если для мод ф(у) использовались граничные условия, соот- ветствующие электрическим стенкам, то для v(у) нужно использовать магнитные стенки и наоборот;
- далее рассчитать константы vk n - 1 ) , ^ аn - 1 ) , vkn ’ r ) , ^ аn ’ r ) , исходя из условия нормировки (14), чтобы окончательно сформировать K у - мод вида (4), соответствующих случаю ТМ-поляризации.
Существенной модификации требует и алгоритм поиска констант распространения и собственно «сшивки» локальных мод в непрерывные функции, описывающие компоненты векторного поля. Для x - локальных мод обеих поляризаций справедливы выражения:
(m,l) (m) (m,l) (m) (m,r)
U ap T p U sp 1 S p U sp ,
(15а)
(m,r) (m) (m,l) (m) (m,r)
U ap -- S p U sp + T p U sp . (15б)
Здесь T pm ) и S pm ) - диагональные матрицы, содержащие следующие элементы:
(m)_/i, /m)m) )2 (m) /tmikUmMm)
T pkk - (k 0 / k pk ) k xpk / tan(k xpk a x ) , (16а)
(m) (m) 2 (m) (m) (m)
S pkk - (k 0 /k pk ) k xpk / sin( k xpk d x ) • (1Об)
Равенства, связывающие значения локальных x -мод обеих поляризаций из соседних столбцов и их производные, приведены ниже:
тт ( m , r ) ( m , m + 1)rr( m + 1, l )
U sh - O hh U sh ,
(17а)
u amr - o hr + 1 u am + 1 ,l) - kzo hmm + 1 U m + 1 ,) , (17б)
Use,r) - oee (m-m+1) Ue+1,1), uam,r) - oem+1m)uam+11) + kzohm+1m)usm+11),(17г)
где матрицы O hm ’ m ) , o km ’ m ) и o hm ’ m ) имеют следующие элементы:
ohmp11 -< ф m W) > ,(18а)
o.k '■< V< ^"(у) >,(18б)
( m , m ') _ , i( m ) I m ') / Д m')(vx > / / ' m )2
o hekp - < V' k I V p / 6 ( у ) > / k hk
+ < фkm)Wpm)! 6(m\у) > / kem1.
Выражение для < ф1( | ф p > через значения функций и производных на границах слоев (константы ф кn , 1 ) , ф an ’ l ) , ф кn , r ) , ф an , r ) ) уже определялось ранее, в рамках скалярного подхода [1]. Далее приведем формулы удобные для расчета элементов остальных матриц интегралов перекрытия:
< V k 1 V p ! 6 ( у ) >-
N ( v sk * r ) v ap r ) - v ankr v sp - r ) - v sk * l v np1 ) + v ak l v sp -1 ) )
U e( n ) ( k kk - k kp )
< < ^ k 1 V p / e (у ) > -
.u ( - Ф a nk1 y-pl ) - kMnl v p, 1 ) + Ф a nr v pr ) + kunr v prr ) ) (20)
U e(n ) ( k kk - k kp ) ’
< фк |vp 1e( у) >- n г -.к) n,l x,/ n.l) _k2,4( n •l L/ n ■l) U-n •r)i//(n,r) +^2 ^( n’r )i// n -r)i
V-i ( — фak v ap k kp ^ k v sp + ф ak v ap + k kp ^ k v sp ) (21)
U 4nw2 2У"х n-1 e (kkk kkp)
Нужно отметить, что введение множителя
Г , k о
I- ( m )
( k pk
, отличающего выражение для x - мод в век- торном случае от скалярного аналога, позволяет, сохранить простое выражения для нормировки (14) локальных у - мод ТМ - поляризации и получать выражения для элементов матриц o^mp) и oemm), которые не зависят от корней характеристических 2
уравнений kpk .
Аналогично задаче отыскания констант распространения для скалярного случая, можно сформулировать задачу решения однородной алгебраической системы уравнений:
Е ( kz )U - 0,
где матрица 3 ( kz ) имеет ленточную структуру и зависит от параметра kz :
|
Ah2) |
с (2) Ch |
B h |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
С ( 2) |
A( (2) |
O |
B( (2) |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
D^ |
0 |
Ah (3) |
Г (3) Ch |
Bh (3) |
0 |
0 |
0 |
0 |
0 |
||
|
н ( k z ) - |
0 |
D( (3) |
С( (3) |
A( (3) |
O |
B( (3) |
0 |
0 |
0 |
0 |
. (23) |
|
0 |
0 |
0 |
0 |
||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
п ( M ) Dh |
0 |
Д ( M ) Ah |
Г ( M ) Ch |
||
|
_ 0 |
0 |
0 |
0 |
0 |
0 |
0 |
Г) ( M ) e |
с ( M ) |
A (M ) _ |
Компоненты блочной матрицы В ( k z ), выражаются через уже определенные матрицы интегралов перекрытия и диагональные матрицы т Рm ) и S ( p m ) .
( m ) ( m , m - 1)т( m - 1) ( m - 1, m ) ( m )
A h - O hh T h O hh + T h ,
A ( m ) = O< m - 1, m ) T jl m - 1) Q< m - 1, m ) + T m )
в случае магнитных стенок выражения для
A (м ) отличаются от общей схемы:
(24а)
(24б)
AР2) и
(2) (2,1) (1) С(1) (1) - 1 С(1) (1,2) I J^2)
Ah - O hh ( T h - S h ( T h ) S h ) O hh + T h ,(24в) A ( 2) - O (^T ( T ® - S «( T ®) -1 S <*>) O^ + T (2\ (24г) A h M - O M M -D T M - 1) O hM - > M + T h M - S h ^TM ) - 1 S M , (24д) A M - O M -I M T M ) O M -I M + T M - S M T M ))-1 S M , (24ж)
|
( m ) Bh |
_ С ( m ) ( m , m + 1) - S h O hh , |
(24е) |
|
( m ) e |
( m ) ( m , m + 1) -- S e O ee , |
(24з) |
|
( m ) Ch |
( m , m - 1) ( m - 1, m ) - kz Ohh Oh( , |
(24к) |
|
( m ) e |
-_t o ( m - 1, m ) T Z1( m , m - 1) T - k z O ee O he , |
(24л) |
|
( m ) Dh |
( m , m - 1) ( m - 1) - O hh S h , |
(24м) |
|
( m ) e |
( m - 1, m ) T (V m - 1) - O ee S e . |
(24н) |
В выражениях (24) индекс m изменяется в диапазоне 2, M .
В свою очередь вектор U в (22), также содержит значения на границах локальных мод как ТЕ, так и ТМ - поляризации.
|
Г ^(2, l ) 1 sh |
||
|
(2, l ) se |
||
|
(3, i ) U sh |
||
|
U - |
(3, l ) se |
. (25) |
П ( M , l ) U sh
( M , l )
se лам (3) рассчитываются компоненты векторного поля ET, E.,, E., cBY, cB., и cB,.
xyz x y z
Расчет векторным методом основной моды слабонаправляющего оптического волновода
Алгоритм расчета векторных мод волноводов, основанный на методе согласованных синусоидальных мод, был реализован с помощью пакета Matlab 6.0.
В качестве тестового примера для проверки работоспособности программной реализации использовалась модель слабонаправляющего круглого волокна с показателем преломления в сердечнике - co - 1,47 и - cl - 1,463 - в оболочке. Структура сечения данной модели изображена на рис. 1.
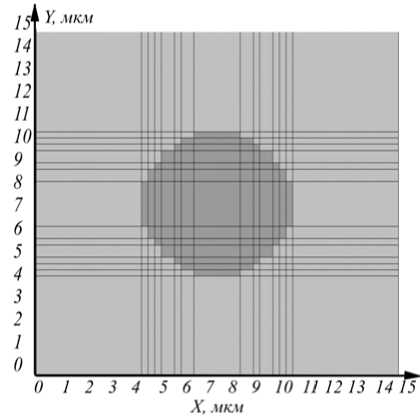
Рис. 1. Модель поперечного сечения круглого слабонаправляющего волновода, темно-серым цветом показаны области со значением показателя преломления —со - 1 , 47 , светло-серым - с —с1 - 1 , 463
Для длины волны излучения X 0 - 1 , 3 мкм был произведен расчет всех шести компонент электромагнитного поля основной моды, которая представляет наибольший интерес в силу того что, исследуемая модель являет собой образец одномодового волокна, поскольку условие многомодовости
Задача (22) решается тем же самым способом, который был предложен для скалярного случая в работе [1]. В результате, после получения константы распространения и доопределения локальных x - мод, из полученного набора функций по форму
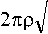
V -
2 . ..2
-co---c- >> 1
X 0
не выполняется. Здесь р- характерный размер сердечника (радиус) равный в данном случае 3 мкм.
V _ 2 п У1,472 + 1,463 2 ■ 3 мкм
1,3 мкм
» 2,078.
На рис. 2 показаны распределения интенсивности рассчитанных компонент.
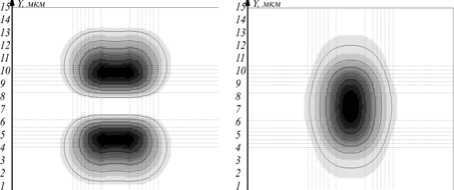
О 12 3 4 5 6 7 8 9 10 II12 13 14 К О 12 3 4 5 6 7 8 9 10 II 12 13 14 Гз X. мкм X. мкм
Таблица 2. Значения интегралов от функции интенсивности компонент основной моды
|
F |
I ( F ) |
|
Ex |
0,3568 |
|
E y |
4,4577 |
|
E z |
-0,0021 |
|
cBx |
9,5642 |
|
cBy |
0,7679 |
|
cBz |
-0,0102 |
Как следует из таблицы 2, наибольший вес имеет компонента cBx , тогда как обе продольные компо- а) Ex
б) Ey
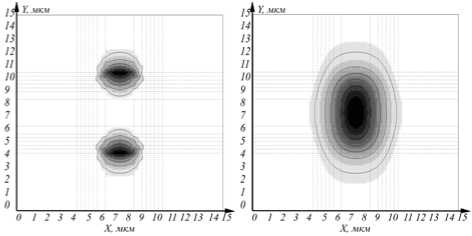
ненты Ez и cBz очень малы.
Полученные функции, описывающие поле основной моды, также подверглись проверке на удовлетворение уравнениям Максвелла:
< — Ez + ikzEx _ ikncBv 9x 0 y
— E +— E _- ikocB d x y d y x 0 z
в) Ez г) cBx
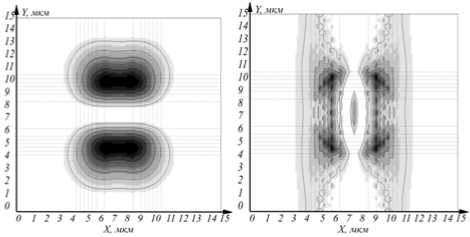
д) cBy
е) cBz
— Bz + ik z B y _ ikй ЕЕ 0 ^ 0 c 2 E x
” —Bz + ik z B x _ - ik 0 EE 0 M 0 c 2 E y , 9x
д
T B y + ^ B x _ ik 0 EE 0 ^ 0 c 2 E z
9x9y
9 „ 9 „, „
— cBx +--cBv - ik,cB, _ 0, xy zz
9x9y
5 г3
- ik z E z
_ 0.
— E x +-- E y
9x дy y
Рис. 2. Распределения интенсивности соответствующих электрических и магнитных компонент основной моды волокна с индексом
к kz- _ 1,4642 k0
Поскольку, как видно из формул (3), компоненты Ez и cBz чисто мнимые, то соответствующие им графики распределения интенсивности были инвертированы, то есть наиболее темному цвету соответствует наименьшее (отрицательное) значение интенсивности, в отличие от графиков остальных компонент, где значение интенсивности всюду положительно.
Оценить масштаб каждой из составляющих помогает таблица интегралов от функции интенсивности по области сечения S :
I ( F ) _ J F ( x , y )|2 dxdy . (27)
S
Среднеквадратическое отклонение между левыми и правыми частями уравнений при подстановке в них рассчитанных компонент составило незначительную величину:
f 0.0005
СКО ( RotE _ - ik 0 cB ) _ ^ 0.0017,
0.0064
I 0.0004
СКО ( RotB _ ik 0 ee 0 ^ 0 c 2 E ) _0.0074 ,
I 0.0053
СКО ( DivB _ 0) _ 0.0094 ,
СКО ( DivE _ 0) _ 0.0046 .
Следовательно, компоненты, полученные с помощью векторного метода согласованных синусоидальных мод, удовлетворяют уравнениям Максвелла с точностью 0,01, то есть рассчитаны верно. Нарушение же радиальной симметрии компонент можно считать следствием использования граничных условий, налагаемых по прямоугольному контуру.
Заключение
В настоящей работе был рассмотрен векторный случай метода согласованных синусоидальных мод, его программная реализация применялась для расчета основной векторной моды круглого слабонаправляющего волокна. Проверка полученного результата с помощью подстановки его в уравнения Максвелла подтвердила правильность расчетов.
Работа выполнена в рамках российско-американской программы « Фундаментальные исследования и высшее образование» (BRHE), а также поддержана президентским грантом РФ НШ-1007.2003.01.


