Расчет виброизоляторов из материала МР с упругодемпфирующими элементами сложной формы методом конечных элементов

bh ³

сила, R - радиус кривизны кольца, J x = 12

–

момент инерции сечения кольца шириной b и толщиной h . Отсюда

E = 0.149 C — p J ,

где Cp = ^ - жесткость кольца бее учета силы трения в направлении оси Y около положения равновесия 5y = 0. Материал МР и кольцо из него обладают нелинейными характеристиками, однако около положения равновесия упругая линия кольца близка к линейной, и можно экспериментально определить

Т +Т

C « ^{1 + 2 p} a1 + a ₂ ,

где T и a - отрезки, отсекаемые петлей гистерезиса соответственно на осях силы и деформации (рис. 2).

Исходный радиус кривизны кольца R ₀ после установки элементов крепления с шириной L меняется. Если бы свободные участки кольца

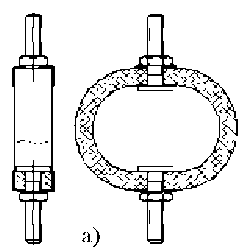
Рис.1. Виброизоляторы из материала МР: а – кольцевого типа, б – колокольчикового типа

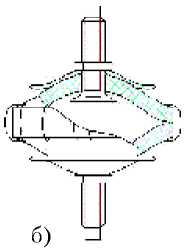
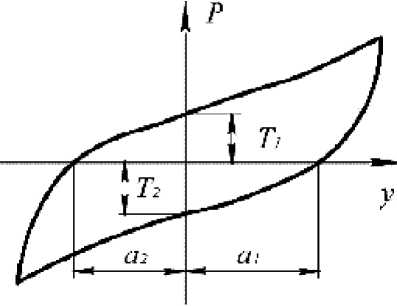
Рис. 2. Петля гистерезиса виброизолятора из МР

имели форму полукруга, радиус их кривизны был бы R1=R0-. Реальный радиус кривизны больше R1 , но меньше R0 , и можно предположить

^{R 0+ R 1} = R - ^L

2⁰ 2 π ^.

Таким образом, для определения эквивалентного модуля упругости материала МР в кольце в направлении оси Y достаточно экспериментально определить петлю гистерезиса кольца в направлении этой оси, найти на ней отрезки T и a , рассчитать значение C_p по формуле (2), значение R по формуле (3), и определить Е по формуле (1).

Модуль Е зависит также от относительной плотности материала МР ρ= ρMR , где ρMR – ρS плотность материала МР, ρS – плотность стали. Первоначально были исследованы кольца с ρ=0,20.

Параметры исследованных колец и полученное значение модуля Е приведены в табл. 1. Ширина элемента крепления для всех колец L = 7 мм.

Среднее значение E = 10,3 Н/мм², отклонения от него могут быть связаны как с погрешно-

Таблица 1. Параметры колец, исследованных для определения значения Е

кольцо Р ММ ь, ММ К мм Е, Н/мм" 1 0,20 9,5 7,3 5,0 10,50 2 0,20 14,5 7,5 5,0 9,15 3 0,20 17.5 7.8 5.0 11.14 стью определения радиуса R, так и с технологическими отклонениями параметров материала МР при изготовлении колец.

Параметры материала МР при сжатии различны в направлении силы прессования и в направлении, перпендикулярном силе прессования материала. Однако можно предположить, что эти различия будут не столь велики при работе материала МР на изгиб, происходящей при деформации кольца. Поэтому можно попытаться воспользоваться эквивалентным модулем упругости в направлении оси Y для расчета упругих характеристик колец в направлении двух других осей.

В принятой системе координат на деформацию кольца оказывает влияние коэффициент Пуассона ν _yx . По данным [2] ν _yx ≤ 0,03 и погрешность в его определении мало влияет на результаты расчета.

Для проверки возможности расчета упругой характеристики кольца при помощи полученного эквивалентного модуля упругости Е были проведены расчеты упругих деформаций колец при помощи конечно-элементной программы ANSYS. Сравнение расчетных деформаций в направлениях различных осей и экспериментально полученных упругих линий для колец из МР различного размера приведены на рис. 3-6. Сплошная линия представляет среднюю линию экспериментально полученной петли гистерезиса, значки – расчет с применением программы ANSYS.

Видно, что погрешность определения деформации (и, соответственно, жесткости) по упругой линии обычно не превышает 10%. Поскольку оп-

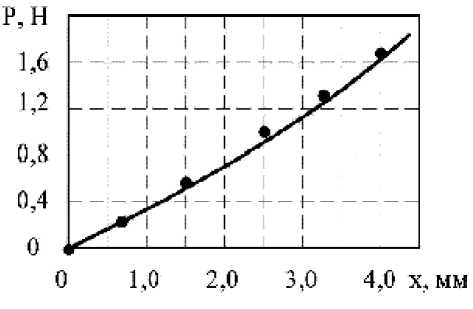
Рис. 3. Упругая линия кольца 1 в направлении оси Х

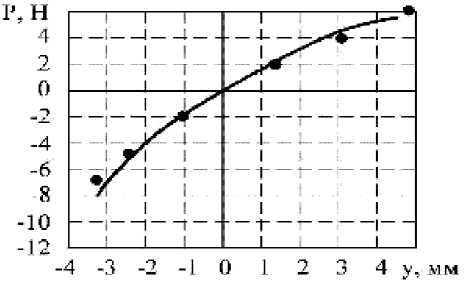
Рис. 4. Упругая линия кольца 1 в направлении оси Y

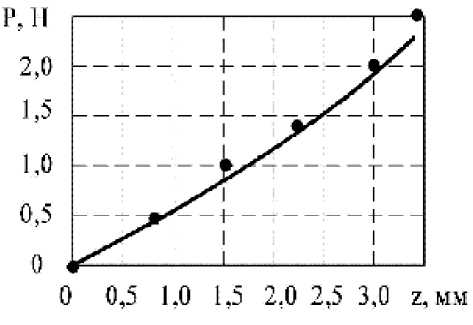
Рис. 5. Упругая линия кольца 1 в направлении оси Z

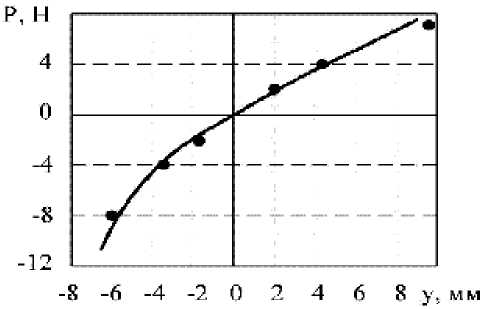
Рис. 6. Упругая линия кольца 3 в направлении оси Y

ределенная по упругой линии жесткость c используется обычно для расчета резонансной час-

тоты виброизолятора to =

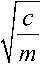
(где m – масса

b= 7 мм, h = 5 мм, р = 0.21 ) дал несколько менее сильную зависимость, приблизительно от d _w ^1,5 , которая хорошо аппроксимируется полиномом

виброзащитной системы), погрешность в 10% при определении жесткости приводит к погрешности 5% при определении резонансной частоты, что можно считать удовлетворительной точностью.

Модуль жесткости зависит также от относительной плотности материала МР и от диаметра проволоки. Для определения зависимости Е от р были исследованы кольца с параметрами, приведенными в табл. 2.

Несмотря на значительные различия значений Е , также связанные с погрешностью определения радиуса R и с технологическими отклонениями параметров материала МР при изготовлении колец, можно получить зависимость модуля Е от относительной плотности материала МР.

E « 54,1 р - 1,68 (МПа).

Жесткость отдельной проволоки пропорциональна четвертой степе н и ее диаметра d_w , но для выполнения условия р = const при изменении диаметра проволоки должно выполняться условие n n 1 d W1 /4 = n n 2 d W2 / 4 (где n 1 , d w 1 и n 2 , d w ₂ - соответственно, старые и новые число контактов и диаметр проволоки). Поскольку число контактов уменьшается пропорционально d w ² , следует ожидать, что значение Е пропорционально d_w ² . Эксперимент на серии колец ( R ₀ = 19 мм,

E » (0,028 - 0,053 dw +

+ 0,45 dW - 1,02 dW ) х 10 4 (МПа).

Предлагаемый подход применим и к коло-кольчиковому виброизолятору. Его упругий элемент представляет собой кольцо криволинейного сечения с внутренним радиусом r ₁ , внешним r₂ и толщиной 5 (рис. 7).

Это кольцо деформируется распределенными нагрузками q ₁ и q ₂ . Известно [4] аналитическое решение о деформировании конического кольца (рис. 8). (Существуют и виброизоляторы из МР с упругодемпфирующим элементом в виде конического кольца [5], для них данное решение будет точным.)

Деформация в осевом направлении при приложении распределенных нагрузок q ₁ и q ₂

Y = ⁽ q 2 r 2^{2 -} q ^r 1^{2)( r} 2^{- r} 1)

EJ ^*

где

J

*

=1 y

F

dF

r

=1

y ₁ ² dF

^^^^^B

F

r

c 2/ ^d F = t r F r

Таблица. 2. Параметры колец, исследов а нных для определения зависимости Е от р

= 5 tga 1(r22 - r,2 ) - 2 r (r2 - r ) + r,2 In r^-cos а ^ 2

, 5 ³           , r₂        2 5 ,r₂

+cos a In — - c In —

12           r1       cos a

+

кольцо	Р	мм	ь, мм	К мм	Е, Н/мм"
4	0,245	14,5	6,0	5,0	11,13
5	0,245	17,5	5,5	5,0	12,15
6	0,273	14,5	6,0	5,0	12,45

c

– параметр геометрии кольца, аналогичный моменту инерции сечения (здесь место расположения центра тяжести сечения

tg a

V

r ₂

^^^^^e

r ₁

^^^^^e

ln r ²

r ₁

a - угол наклона конуса).

r ₁

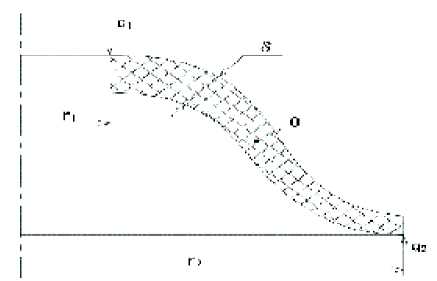
Рис. 7. Сечение упругодемпфирующего элемента виброизолятора колокольчикового типа

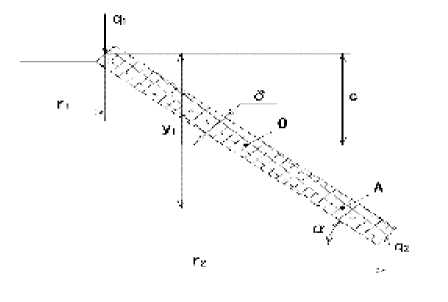
Рис. 8. Расчетная схема конического кольца

Для криволинейных профилей колокольчиковых виброизоляторов параметр J ^* можно определить численным интегрированием.

Распределенные нагрузки q1 и q2 в осевом направлении создают силы Q1 = 2nr q 1 и Q 2 = 2nr2 q 2 соответственно. Поскольку Q1 = Q2 = Q , получаем q = Q q = Q

⁴¹ 2 n r 1 ; ^² 2 n r ₂ . (6)

Подставив (6) в (4), получим

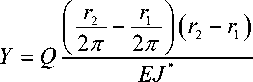
Таким образом, жесткость конического кольца из МР без учета сил трения

CF

Q _ 2nEJ

Y " ( Г 2 - r j² ■

Отсюда можно выразить эквивалентный модуль упругости материала

E _

C f ( Г 2 — Г 1 ) ²

2 n J *

тально исследован колокольчиковый виброизолятор со следующими параметрами: вес упруго-демпфирующего элемента 21,73 грамма, объем 0,124 x 10 ⁴ м ³ , диаметр проволоки материала МР 0,15 мм, r 1 = 4,25 мм, r₂ = 24 мм, 5 в криволинейном профиле изменяется от 4 до 8 мм, для расчета кольца было принято 5 = 5 мм, а _ 34⁰ . По петле гистерезиса было получено k = 14 Н/мм . Таким образом, Е= 5,24 МПа. Для изгиба для сходной плотности материала МР получено Е= 12 МПа, эксперимент по сжатию дает значение Е= 2,3 МПа. В колокольчиковом виброизоляторе материал МР работает на сжатие и на изгиб одновременно, поэтому полученное значение Е согласуется с этими результатами.

Полученное значение E было использовано для расчета деформации программой ANSYS. При расчете учитывалась нелинейность конструкции в результате больших перемещений. Экспериментально полученная и расчетная упругие линии петли приведены на рис. 9.

Хорошее совпадение результатов показывает, что с использованием эквивалентного модуля упругости можно рассчитывать методом конечных элементов виброизоляторы сложной геометрической формы, в которых материал МР

Жесткость без учета сил трения можно определить экспериментально около положения равновесия по петле гистерезиса, используя уравнение (2). Подставив ее в (9), получим значение эквивалентного модуля упругости.

Вследствие переменности параметра J ^* этот модуль будет зависеть от размеров виброизолятора. Однако для данного размера виброизолятора он определятся один раз и позволяет рассчитывать методом конечных элементов деформацию виброизолятора при больших амплитудах вибрации (где сказывается влияние нелинейности), при сложном нагружении – одновременно в осевом и радиальном направлении, прецессионное нагружение вращающимся вектором силы.

Для проверки результатов был эксперимен-

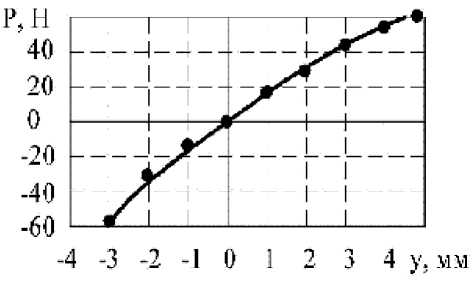
Рис. 9. Экспериментально полученная (сплошная линия) и расчетная (точки) упругие линии петли гистерезиса колокольчикового виброизолятора

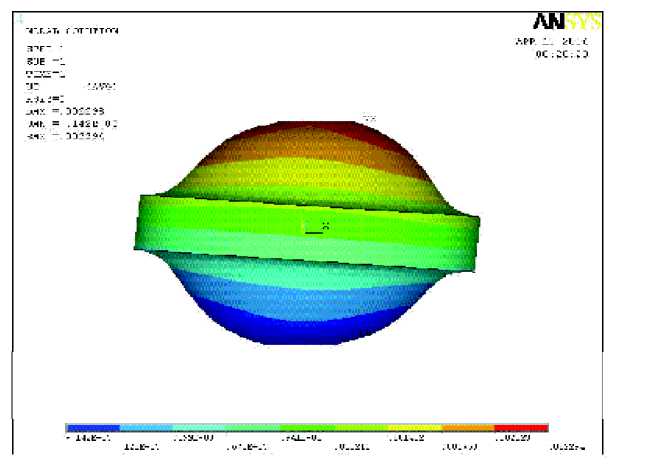
Рис. 10. Расчет колокольчикового виброизолятора на сдвиг программой ANSYS

имеет сложное напряженное состояние. Было рассчитано нагружение виброизолятора на сдвиг в направлении оси Х силой 30 Н. Полученное при помощи программы ANSYS максимальное значение деформации 2,3 мм (рис. 10), экспериментально полученное 2,1 мм.

Таким образом, определение эквивалентного модуля упругости в области малых деформаций позволяет рассчитывать методом конечных элементов виброизоляторы любой сложной формы, в которых материал МР имеет сложное напряженное состояние (изгиб со сжатием, изгиб со сдвигом), при сложном напряженном состоянии и при больших амплитудах деформации. Основаниями для определения эквивалентного моду- ля упругости являются аналитическое решение для тела более простой формы и эксперимент.