Расчет временных характеристик системы массового обслуживания с процессами расщепления и слияния заявок и разогревом

В последние годы все большее распространение получают технологии распределенной обработки данных в реальном масштабе времени. Примером применения такой технологии в сфере обработки данных дистанционного зондирования Земли (ДЗЗ) является создание единой территориально распределенной системы (ЕТРИС) ДЗЗ. Эта система позволяет перейти к распределенной обработке данных со всех типов космических аппаратов (КА) ДЗЗ с использованием универсальных комплексов приема информации [5]. Данные подходы предполагается реализовать с помощью создания унифицированных программных комплексов распределенной обработки, хранения и распространения данных ДЗЗ, функционирующих на вычислительных кластерах пунктов приема информации или в центрах обработки данных.

Текущими проблемными вопросами дальнейшего развития технологии распределенной обработки данных являются увеличение объема обрабатываемых данных и недостаточная пропускная способность каналов передачи.

Например, в сфере обработки информации с КА ДЗЗ увеличение объема данных наблюдения вызвано повышением пространственного разрешения космических снимков

Расчет временных характеристик системы массового обслуживания ...

с--------------------------------------------------------------------------------------------------------------

Хабаров Роман Сергеевич начальник лаборатории военного института (научно-исследовательского) Военнокосмической академии им. А.Ф. Можайского. Сфера научных интересов: исследование операций, теория очередей, машинное обучение. Автор 11 опубликованных научных работ.

и использованием многоспектральной и гиперспектральной съемки. Существует практическая необходимость обработки и интерпретации таких данных в реальном масштабе времени, например при космическом мониторинге чрезвычайных ситуаций [7]. В связи с этим остро встает проблема оперативной передачи гиперспектральных данных по радиоканалам с ограниченной пропускной способностью. Существенную роль приобретает соотношение между информационной производительностью аппаратуры ДЗЗ и пропускной способностью используемых радиоканалов передачи информации [4].

Анализ оценок информационной производительности современных КА ДЗЗ с гиперспектральной съемкой показывает, что передача видеоданных с КА на наземные пункты приема информации в масштабе времени, близком к реальному, требует обеспечения скорости передачи информации в сотни мегабит – единицы гигабит в секунду. В существующих и перспективных спутниковых системах передачи видеоданных с КА ДЗЗ скорости передачи информации составляют сотни мегабит в секунду. Однако эти возможности систем передачи информации уже сейчас не согласуются с информационными возможностями многих гиперспектральных систем ДЗЗ, в перспективе это рассогласование будет только усиливаться [4].

В связи со сложившейся ситуацией все большую актуальность приобретают вопросы оценивания оперативности проектируемых систем распределенной обработки данных, функционирующих в реальном масштабе времени, с учетом временных задержек на прием информации. Особую сложность представляет тот факт, что оценка оперативности таких систем в виде среднего времени обработки, как правило, является недостаточной, и требуется получить оценку вероятности превышения (непревышения) директивно заданного времени.

Методы обработки данных

В [3] отмечается, что, несмотря на наличие различных подходов к анализу работы вычислительных сетей (математический аппарат теории графов и сетевого анализа, теории нечетких множеств и нечеткой логики, тензорного анализа, теории фракталов), методически разработанным и применяемым на практике математическим аппаратом является теория очередей. При моделировании распределенной обработки данных с учетом задержки на время их приема и (или) восстановление необходимо учитывать также следующие особенности:

• •    обработка осуществляется параллельно на заданном наборе серверов;

• •    каждый сервер результаты своей работы записывает в отдельный файл, после чего выполняются их «склеивание» и дальнейшая интерпретация результатов выполнения.

Подобный процесс разделения задачи на подзадачи с параллельным их выполнением и последующим объединением результатов традиционно называется Split-Join. На рисунке 1 изображена схема процесса обработки по технологии Split-Join применительно к данным ДЗЗ. Общее время выполнения такой задачи определяется длительностью этапов ее декомпозиции и объединения результатов, а также временем решения самой трудоемкой из подзадач.

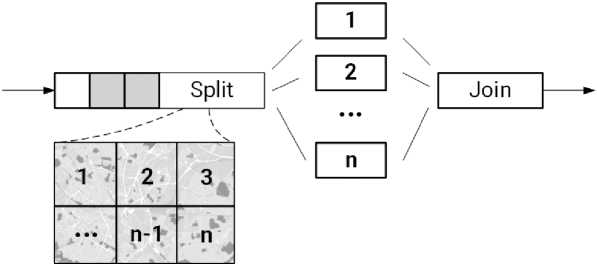
Рис. 1. Схема процесса обработки с разделением и слиянием задач

На рисунке 2 в качестве примера изображена циклограмма обработки данных ДЗЗ, полученных в текущем сеансе связи, в процессе выдачи восстановленной информации с распределением по серверам обработки. В общем случае время восстановления одной части принятых данных τ является случайной величиной. Из представленного рисунка видно, что время обработки всего объема принятых в текущем сеансе связи данных без учета временных затрат на операции «склеивания» и интерпретации результатов определяется моментом завершения обработки последнего фрагмента t _max. Такие дополнительные временные затраты на обслуживание при поступлении заявок в свободную систему в теории очередей традиционно называются процессами «разогрева».

На рисунке 3 изображена циклограмма для случая одновременной обработки данных сеанса связи после завершения восстановления всей принятой информации. Поскольку для операции восстановления, как правило, выделяются отдельные сервера, при поступлении данных в занятую систему процесс восстановления происходит во время ожидания начала обработки и не оказывает влияния на оперативность обработки данных в целом.

Расчет временных характеристик системы массового обслуживания ...

n-1

n

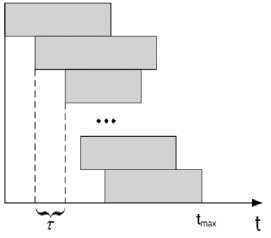
Рис. 2. Циклограмма обработки данных в процессе выдачи восстановленной информации

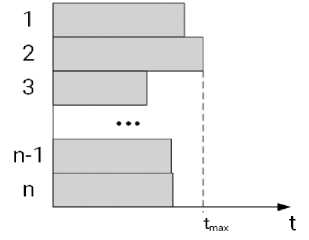
Рис. 3. Циклограмма обработки данных после завершения восстановления информации

Несмотря на то, что процессам Split-Join посвящено достаточно большое количество работ [8–16], вопросы оценивания времени пребывания в системах массового обслуживания (СМО) с процессами Split-Join, а также с «разогревом» до сих пор не освещены. В данной работе предлагается алгоритм расчета СМО с процессами Split-Join и «разогревом», позволяющий получить начальные моменты времени пребывания заявок в системе.

Постановка задачи

Будем считать, что заданы начальные моменты времени обработки фрагмента данных в канале b_j , j = 1, m. Поток поступления заявок будем считать простейшим с интенсивностью λ . Заданы начальные моменты времени задержки, вызванной операциями приема и восстановления части информации a_j , j = 1, m . Число каналов обработки – n . Дисциплина обслуживания в СМО – Split-Join. Требуется найти начальные моменты времени пребывания в системе v_j , j = 1, m .

Для оценки вероятности превышения директивно заданного времени необходимо по найденным моментам v_j , j = 1, m рассчитать параметры аппроксимирующего распределения (например, Вейбулла) и получить значение дополнительной функции распределения (ДФР) при заданном значении требуемого времени обработки.

Алгоритм расчета

Расчет начальных моментов времени пребывания в представленной СМО предлагается осуществить в два этапа. На первом этапе произведем расчет начальных моментов времени обработки с учетом разделения и слияния задач для двух случаев:

• 1 . Обработка осуществляется после прибытия заявки в свободную систему. Расчет начальных моментов времени обработки g_j *, j = 1, m необходимо производить с учетом временных задержек на прием и восстановление.

Обработка данных осуществляется синхронно без учета задержки на прием и восстановление. Соответствующие начальные моменты времени обработки g_j , j = 1, m представляют собой начальные моменты распределения максимума из n случайных величин времен обработки части данных в канале и могут быть рассчитаны по формулам, представленным в [8]:

Методы обработки данных

r gj = jZtk-1 AkF ^k) et ’                             (1)

k = 1

где для {xk} и {Ak} существуют справочные таблицы [3] для различных значений r, а F*(t) представляет собой ДФР распределения максимума времени обработки в n каналах, функция которого определяется как n F *( t) =П F (t), i=1

где F_i ( t ) – функция распределения времени обслуживания в i -м канале.

После получения упомянутых начальных моментов становится возможным представить весь процесс обработки в виде одноканальной системы массового обслуживания типа M/G/ 1 с начальными моментами времени обслуживания в канале g_j , j = 1, m и начальными моментами времени «разогрева» g_j *, j = 1, m .

На втором этапе производится непосредственный расчет начальных моментов времени пребывания заявок в системе v_j , j = 1, m дифференцированием в нуле соответствующего преобразования Лапласа – Стилтьеса (ПЛС), которое определяется выражением [7]

v ^{( s} ) = p 0

a-^M s hM

¹ - sA - e⁽ s )

где p ^*₀ = 1/(1 + λT_B ), T_B = b ^*(1 – λb ); β( s ), β^*( s ) – ПЛС времени обслуживания, соответственно, без «разогрева» и с «разогревом»; b , b ^* – математические ожидания времени обслуживания без «разогрева» и с «разогревом» соответственно.

Осталось указать способ расчета g_j *, j = 1, m . Далее предлагается рассмотреть отдельно варианты расчета для случаев детерминированной и случайной задержки на время приема и восстановления части данных.

Расчет начальных моментов распределения максимума при детерминированной задержке

Как видно из рисунка 2, при детерминированной задержке начало обслуживания в j -м канале будет сдвинуто относительно момента начала обслуживания на время jτ . Таким образом, расчет g_j *, j = 1, m для случая детерминированной задержки осуществляется согласно

r

gj=j^ tk-1 AkG *(tk) et, k=1

где

n

G(tk,t)=1—nF(tk,iT)’ F(tk,т)= i=1

' 0, t k < ^T, F ⁽ t k ^{- T} ),

t k ^ ^T •

Расчет начальных моментов распределения максимума при случайной задержке

При заданных начальных моментах a_j , j = 1, m времени приема и восстановления части информации τ начальные моменты времени задержки начала обслуживания в j -м канале

Расчет временных характеристик системы массового обслуживания ...

am*,j. будут определяться j-кратной сверткой τ, а начальный момент m порядка времени обработки в j-м канале определяется на основании символьного представления gm,j = (b + a*j)m, m = 1,2,…, (3) где после развертывания бинома степени переводятся в номера соответствующих начальных моментов. Дальнейший расчет можно осуществлять по формуле (1), при этом для каждого канала по найденным с помощью (3) начальным моментам gm,j осуществляется подбор по методу моментов параметров аппроксимирующей функции распределения времени обработки в канале с учетом задержек. В качестве аппроксимирующей функции может выступать гамма-распределение, позволяющее выровнять два первых начальных момента при произвольных значениях коэффициента вариации.

Экспериментальная проверка точности расчета начальных моментов времени обработки с расщеплением и слиянием заявок и задержкой начала обслуживания

Верификация предложенного алгоритма расчета производилась сравнением результатов, полученных с помощью формул (1)–(3) с данными имитационного моделирования (ИМ). Приведем здесь пример расчета в сравнении с данными ИМ для следующих исходных данных:

• •    исходная заявка разделяется на 3 подзадачи;

• •    случайная длительность выполнения каждой задачи задана гиперэкспоненциальным распределением второго порядка ( H ₂-распределение) с параметрами y ₁ = 0,3, y ₂ = 0,7, μ ₁ = 0,15, μ2 ₁ = 0,7.

При детерминированной задержке параметр τ был задан равным 0,5. При случайной задержке начала обслуживания были заданы первые три начальные моменты времени задержки a_j – {0,5, 2,0, 10,0} соответственно.

Полученные результаты сопоставлены с результатами имитационного моделирования и представлены в таблицах 1 и 2. Символом σ обозначено среднеквадратическое отклонение времени пребывания заявок в системе. Для численного расчета представлены собственно значения моментов, а также абсолютная и относительная погрешность, обозначенные ∆ и δ соответственно.

Таблица 1

Результаты расчетов при детерминированной задержке

	ИМ	Численный расчет
		Знач.	∆	δ, %
b 1	6,638	6,571	6,67e-2	1,02
σ	0,414	0,429	1,49e-2	3,48
b 3	525,8	519,9	5,96	1,15

Таблица 2

Результаты расчетов при случайной задержке

	ИМ	Численный расчет
		Знач.	∆	δ, %
b 1	10,34	10,18	1,63e-1	1,60
σ	0,397	0,432	3,58e2	8,27
b 3	1696	1758	6,19e1	3,52

Как видно из таблиц 1 и 2, результаты численных расчетов хорошо согласуются с результатами имитационного моделирования.

Методы обработки данных

Расчет начальных моментов времени пребывания в системе

Найденные на предыдущем этапе начальные моменты времени обработки с учетом задержки позволяют перейти к расчету СМО.

Проверку точности расчета приведем для тех же исходных данных. Зададим интенсивность входящего потока λ = 0,12. При таком значении λ обеспечивается коэффициент загрузки СМО, равный 0,75. В таблицах 3 и 4 представлены результаты расчетов для начальных моментов времени пребывания в системе v_j , j = 1,3 при детерминированной и случайной задержке соответственно.

Согласно [2], для оценок первого момента считается допустимой погрешность 20, второго – 40, третьего – 60%. Погрешности расчетных значений не превысили указанных требований. Заметим, что ИМ не является эталоном, поскольку датчики равномерно распределенных чисел не идеальны, а конечные результаты содержат статистическую погрешность.

Таблица 4

Таблица 3

Начальные моменты времени пребывания в СМО при детерминированной задержке

	ИМ	Численный расчет
		Знач.	∆	δ, %
v 1	26,36	24,92	1,441	5,467
v 2	1365	1204	161,3	11,81
v 3	1,06e5	8,62e4	1,96e4	18,51

Начальные моменты времени пребывания в СМО при случайной задержке

	ИМ	Численный расчет
		Знач.	∆	δ, %
v 1	26,54	25,20	1,337	5,036
v 2	1363	1220	142,7	10,46
v 3	1,04e5	8,74e4	1,62e4	15,59

На рисунке 4 представлен график ДФР времени пребывания заявки в СМО, построенный аппроксимацией распределением Вейбулла. Параметры распределения подбирались с помощью метода моментов по найденным на предыдущем шаге значениям v_j , j = 1,3. Полученные графики ДФР позволяют оценить вероятность превышения директивно заданного времени.

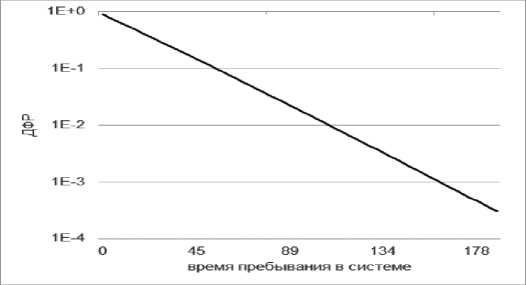
Рис. 4. ДФР времени пребывания заявок в системе

Расчет временных характеристик системы массового обслуживания ...

Заключение

Предложены модель и реализующий ее алгоритм расчета начальных моментов времени пребывания в СМО с процессами расщепления и слияния заявок и «разогревом». Представленная модель позволяет оценить оперативность (среднее время обработки, высшие моменты, вероятность превышения директивно заданного времени) проектируемых систем распределенной обработки данных, функционирующих в реальном масштабе времени, с учетом временных задержек на прием и восстановление информации.